A small area is removed from a uniform spherical shell of mass M and radius R. Then the gravitatioinal field intensity near the hollow portion is
GMR2
GM2R2
3GM2R2
zero
To solve the problem of finding the gravitational field intensity near the hollow portion of a uniform spherical shell from which a small area has been removed, we can follow these steps:
1. Understanding the Gravitational Field Inside a Spherical Shell:
- According to the shell theorem, the gravitational field inside a uniform spherical shell is zero. This means that if we are inside the shell, the gravitational field intensity due to the shell itself is zero.
Hint: Recall that the gravitational field inside a uniform spherical shell is zero regardless of the mass distribution as long as it is uniform.
2. Analyzing the Removed Area:
- When a small area is removed from the shell, we need to consider the gravitational field due to the remaining part of the shell and the effect of the removed area.
- The gravitational field intensity due to the remaining part of the shell (denoted as ER) will still be zero at the center of the shell because the mass distribution is still symmetric around that point.
Hint: Consider how the symmetry of the remaining mass affects the gravitational field.
3. Field Due to the Removed Portion:
- The removed portion can be thought of as a small mass that would have contributed to the gravitational field. The gravitational field intensity due to this small area (denoted as Ecell) will point towards the center of the shell since it is attracting mass towards itself.
Hint: Remember that the gravitational field due to a mass points towards the mass itself.
4. Net Gravitational Field Inside the Hollow Portion:
- Since the gravitational field inside the shell is zero due to the remaining mass, the net gravitational field intensity near the hollow portion will be equal to the gravitational field intensity due to the removed portion.
- Therefore, we can write:
Enet=Ecell−ER
Since ER=0 (inside the shell), we have:
Enet=Ecell
Hint: Consider how the gravitational fields from different sources combine vectorially.
5. Calculating the Gravitational Field:
- The gravitational field intensity Ecell due to the removed area can be calculated using the formula:
Ecell=GMR2
- This is the field due to a mass M at a distance R from the center of the shell.
Hint: Use the formula for gravitational field intensity due to a point mass.
6. Final Result:
- Therefore, the gravitational field intensity near the hollow portion of the spherical shell is:
Enet=GMR2
Conclusion:
The gravitational field intensity near the hollow portion of the spherical shell is equal to the gravitational field intensity due to the removed area, which is given by Enet=GMR2.
- According to the shell theorem, the gravitational field inside a uniform spherical shell is zero. This means that if we are inside the shell, the gravitational field intensity due to the shell itself is zero.
- When a small area is removed from the shell, we need to consider the gravitational field due to the remaining part of the shell and the effect of the removed area.
- The gravitational field intensity due to the remaining part of the shell (denoted as ER) will still be zero at the center of the shell because the mass distribution is still symmetric around that point.
- The removed portion can be thought of as a small mass that would have contributed to the gravitational field. The gravitational field intensity due to this small area (denoted as Ecell) will point towards the center of the shell since it is attracting mass towards itself.
- Since the gravitational field inside the shell is zero due to the remaining mass, the net gravitational field intensity near the hollow portion will be equal to the gravitational field intensity due to the removed portion.
- Therefore, we can write:
Enet=Ecell−ER
Since ER=0 (inside the shell), we have:
Enet=Ecell
- The gravitational field intensity Ecell due to the removed area can be calculated using the formula:
Ecell=GMR2
- This is the field due to a mass M at a distance R from the center of the shell.
- Therefore, the gravitational field intensity near the hollow portion of the spherical shell is:
Enet=GMR2
The gravitational field intensity near the hollow portion of the spherical shell is equal to the gravitational field intensity due to the removed area, which is given by Enet=GMR2.
Topper's Solved these Questions
Similar Questions
Intensity of gravitational field inside the hollow spherical shell is
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
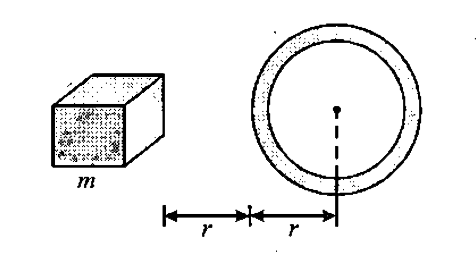
A. only gravitational field inside the shell is zero
B. gravitational field and gravitational potential both are zero inside the shell
C. gravitational potential as well as gravitational field inside the shell are not zero .
D. can't be ascertained
View Solution
Knowledge Check
A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
AGMRB−GMRC−4GMRD−2GMR
For a given uniform spherical shell of mass M and radius R find gravitational field at a distancer r from centre in following two cases (a) r≥R (b) r<R .
View SolutionA solid shere of mass m and radius r is placed inside a hollow spherical shell of mass 4m and radius 4r find gravitational field intensity at
(a) r<y<2r (b) 2r<y<8r (c) y>8r
here coordinate is measured from the point of contact of the sphere and the shell
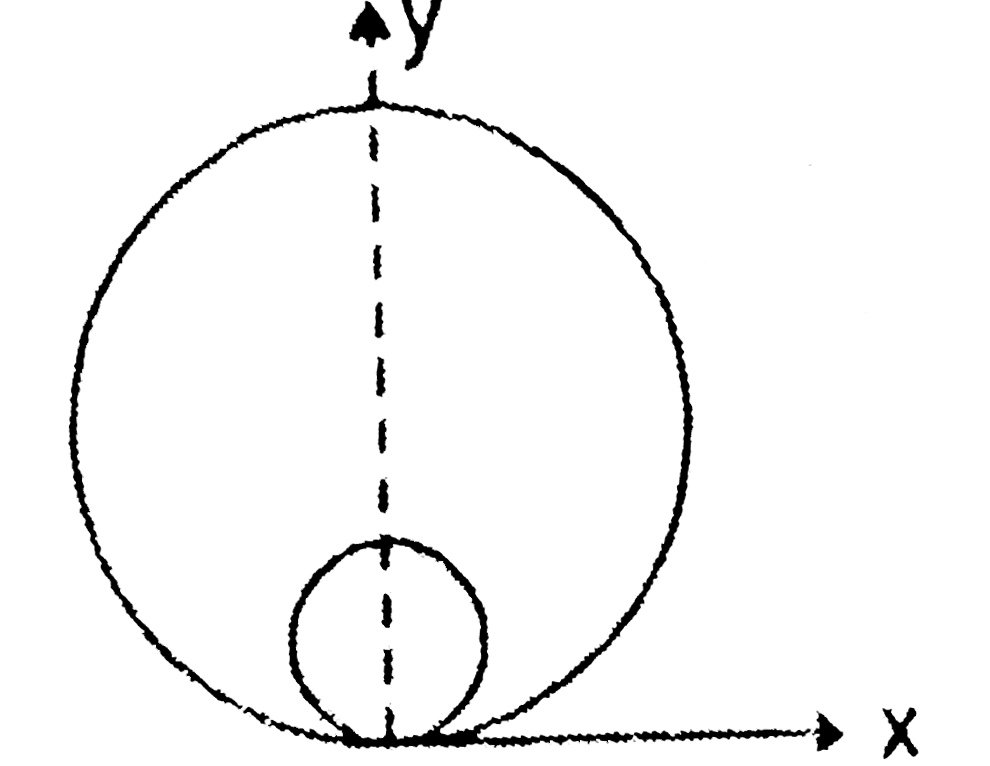 .
.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the center.
View SolutionA uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherical shell of equal mass and radius 2a.Find the gravitational field at a distance a. 32a from the center , b. 52a from the center.
View SolutionA uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherical shell of equal mass and radius 2a. Find the gravitational field at a distance a). 3/2 a from the centre , b). 5/2 as from the centre.
View Solution
