Consider an Atwood machine with both the masses at the same level as shown in Fig. 3E.15. Use the principle of conservation of energy to find
(a) speed of either of the masses as a function of its position and
(b) the acceleration of either of the masses.
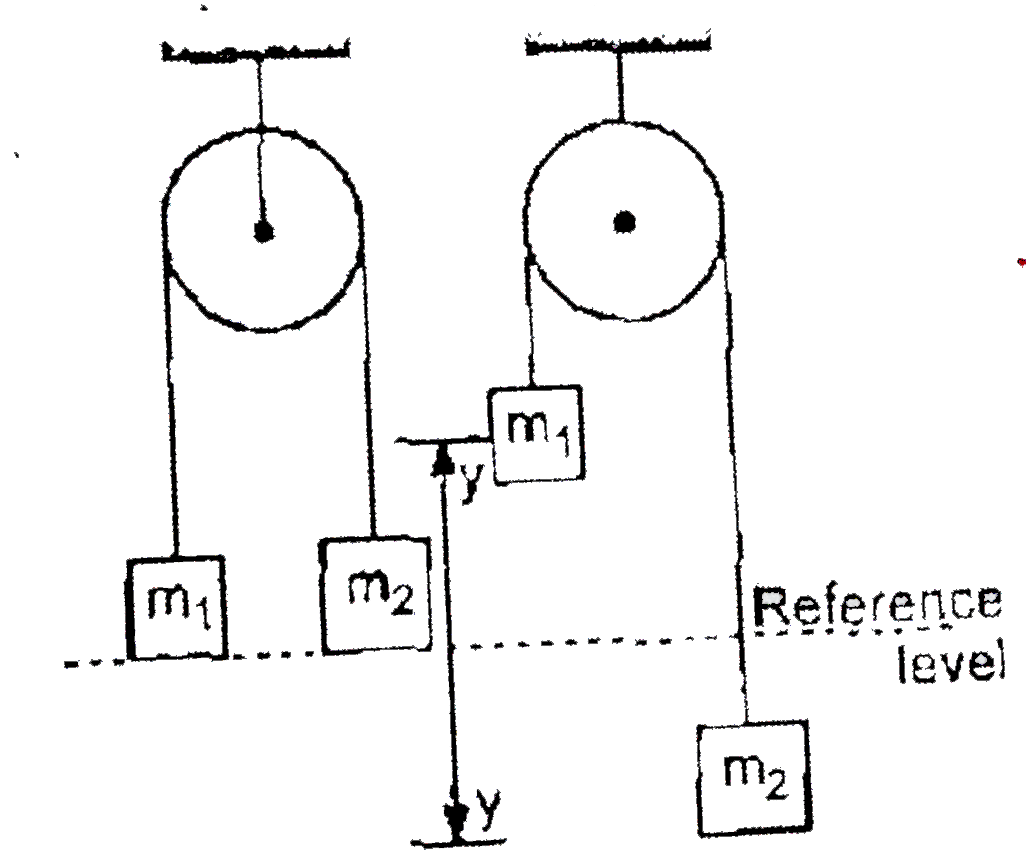
Step by step video & image solution for Consider an Atwood machine with both the masses at the same level as shown in Fig. 3E.15. Use the principle of conservation of energy to find (a) speed of either of the masses as a function of its position and (b) the acceleration of either of the masses. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK AND ENERGYBook:ANURAG MISHRAChapter:WORK AND ENERGYExercise:Level 1
Explore 53 Videos
- WORK AND ENERGYBook:ANURAG MISHRAChapter:WORK AND ENERGYExercise:Level 2
Explore 18 Videos
- WORK AND ENERGYBook:ANURAG MISHRAChapter:WORK AND ENERGYExercise:Matching types problems
Explore 14 Videos
- UNIT AND DIMENSIONSBook:ANURAG MISHRAChapter:UNIT AND DIMENSIONSExercise:Matching Type Problem
Explore 4 Videos
Similar Questions
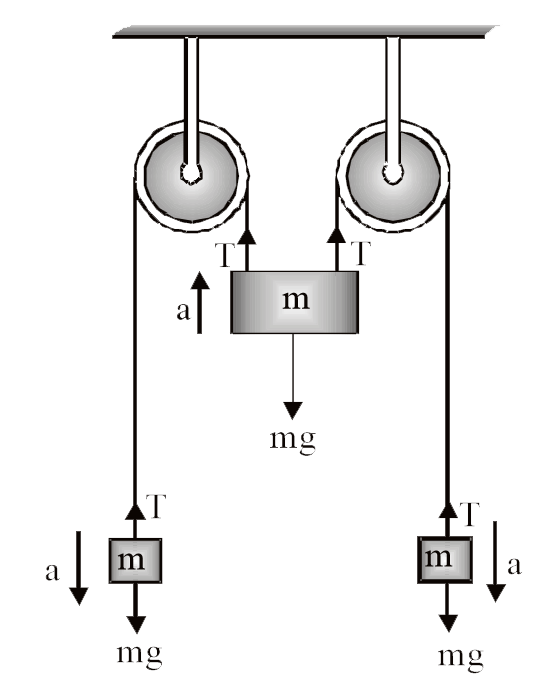
Consider the double Atwood’s machine as shown in the figure. What is acceleration of the masses ?
View SolutionA mass of 0.5 kg is hung from a spring. Agradually increasing 0.5 N force is reuired topull the mass downward a distance of 0.25 m from its equilibrium position,if the mass s then released from this position, find
(a) The total energy of the system .
(b) The frequency of the oscillation
(c ) The speed and acceleration of the mass as it passes the equilibrium position.
(d) The speed and acceleration of the mas when the diplacement from equilibrium is 0.25 m
(e) For the initial condition stated, write down the diplacement equation of motion for this mass.
View Solution
Knowledge Check
A small mass m starts from rest and slides down the smooth spherical surface of F. Assume zero potential energy at the top. Find
(a) the change in potential energy,
(b) the kintic energy,
(c) the speed ot the mass as a function of the angle θ made by the radius through the mass with the vertical.A−mgR(1−cosθ), mgR(1−cosθ), v=√2gR(1−cosθ)B−mgR(1+cosθ), mgR(1−cosθ), v=√2gR(1−cosθ)C−mgR(1−cosθ), mgR(1+cosθ), v=√2gR(1−cosθ)D−mgR(1−cosθ), mgR(1−cosθ), v=√2gR(1+cosθ)
Two masses m and 2m are connected by a massless string, which passes over a pulley as shown in figure. The masses are held initially with equal lengths of the strings on either side of the pulley. Find the velocity of masses at the instant the lighter mass moves up a distance of 15m. ( g=10m/s2 )
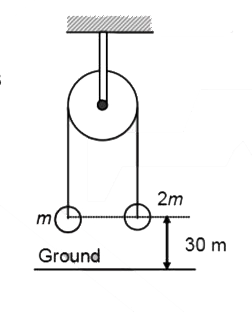
View Solution
A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.
View SolutionA force →F acts on two particles of masses m and 4.0m moving at the same speed but at right angles to each other, as shown in Fig. The force acts on both the particles for a time T. Consequently, the particle of mass m moves with a velocity 4v in its original direction. (a) Find the new velocity v' of the other particle. (b) Also find the change in the kinetic energy of the system.
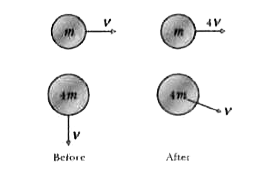
View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionConsider the double Atwood's machine as shown in the figure
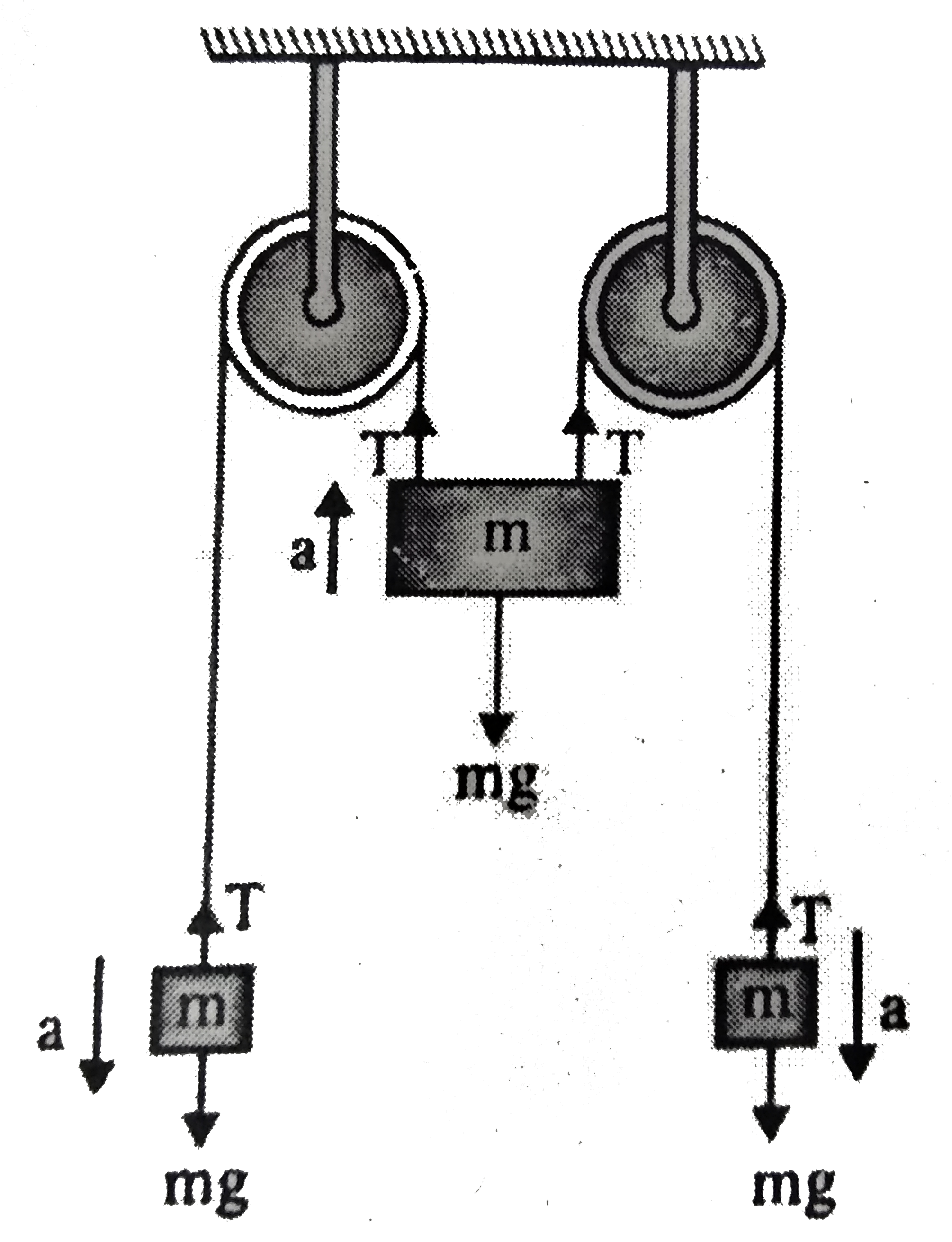
(a) What is acceleration of the masses?
(b) What is the tension in each string?
View SolutionTwo bodies A and B each of mass m are fixed together by a massless spring . A force F acts on the mass B as shown in fig .3 (a)18. At the instant shown , the body A has an acceleration a What is the acceleration of B ?

View SolutionIn an atwood machine the two blocks have massess 1kg and 3kg. The pulley is massless and frictionless and string is light. The acceleration of the centre of mass (in m/s2) of this system is 0.5x. Find the value of x.
View Solution
