Consider an electron in front of metallic surface at a distance d (treated as an infinite plane surface). Assume the force of attraction by the plate is given as 14q24π∈0d2.
Calculate work in taking the charge to an infinite distance from the plate. Taking d=0.1nm, find the work done in electron volts. [Such a force law is not valid for d lt 0.1nm].
To solve the problem of calculating the work done in taking an electron from a distance d (0.1 nm) to an infinite distance from a metallic surface, we can follow these steps:
Step 1: Understand the Force of Attraction
The force of attraction F between the electron and the metallic surface is given by the formula:
F=q24πϵ0d2
where:
- q is the charge of the electron (q=1.6×10−19C)
- ϵ0 is the permittivity of free space (ϵ0≈8.85×10−12C2/N m2)
- d is the distance from the plate (0.1 nm = 0.1×10−9m)
Step 2: Set Up the Work Done Calculation
The work done W in moving the electron from distance d to infinity can be calculated using the integral of the force over the distance:
W=∫∞dFdx
Since the force depends on x (the distance from the plate), we can express the work done as:
W=∫∞dq24πϵ0x2dx
Step 3: Perform the Integration
The integral can be computed as follows:
W=q24πϵ0∫∞d1x2dx
The integral of 1x2 is:
∫1x2dx=−1x
Thus, we evaluate the limits:
W=q24πϵ0(−1x)∞d=q24πϵ0(0−(−1d))=q24πϵ0d
Step 4: Substitute Known Values
Now substituting the known values:
- q=1.6×10−19C
- d=0.1×10−9m
- ϵ0=8.85×10−12C2/N m2
Calculating W:
W=(1.6×10−19)24π(8.85×10−12)(0.1×10−9)
Step 5: Calculate the Numerical Value
Calculating the numerator:
(1.6×10−19)2=2.56×10−38
Calculating the denominator:
4π(8.85×10−12)(0.1×10−9)≈1.11×10−20
Thus:
W≈2.56×10−381.11×10−20≈2.31×10−18J
Step 6: Convert Joules to Electron Volts
To convert the work done from Joules to electron volts:
1eV=1.6×10−19J
W≈2.31×10−181.6×10−19≈14.44eV
Final Answer
The work done in taking the electron to an infinite distance from the plate is approximately:
14.44eV
The force of attraction F between the electron and the metallic surface is given by the formula:
F=q24πϵ0d2
where:
- q is the charge of the electron (q=1.6×10−19C)
- ϵ0 is the permittivity of free space (ϵ0≈8.85×10−12C2/N m2)
- d is the distance from the plate (0.1 nm = 0.1×10−9m)
The work done W in moving the electron from distance d to infinity can be calculated using the integral of the force over the distance:
W=∫∞dFdx
Since the force depends on x (the distance from the plate), we can express the work done as:
W=∫∞dq24πϵ0x2dx
The integral can be computed as follows:
W=q24πϵ0∫∞d1x2dx
The integral of 1x2 is:
∫1x2dx=−1x
Thus, we evaluate the limits:
W=q24πϵ0(−1x)∞d=q24πϵ0(0−(−1d))=q24πϵ0d
Now substituting the known values:
- q=1.6×10−19C
- d=0.1×10−9m
- ϵ0=8.85×10−12C2/N m2
W=(1.6×10−19)24π(8.85×10−12)(0.1×10−9)
Calculating the numerator:
(1.6×10−19)2=2.56×10−38
Calculating the denominator:
4π(8.85×10−12)(0.1×10−9)≈1.11×10−20
Thus:
W≈2.56×10−381.11×10−20≈2.31×10−18J
To convert the work done from Joules to electron volts:
1eV=1.6×10−19J
W≈2.31×10−181.6×10−19≈14.44eV
The work done in taking the electron to an infinite distance from the plate is approximately:
14.44eV
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SHORT ANSWER TYPE QUESTIONS6videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Very Short Answer Type Question.20videos
CURRENT ELECTRICITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Long Answer Type Question6videos
ELECTRIC CHARGES AND FIELD
Similar Questions
A charge Q is fixed at a distance d in front of an infinite metal plate. The lines of force are represented by
 View Solution
View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View SolutionA capacitor is given a charge q. The distance between the plates of the capacitor is d. One of the plates is fixed and the other plate is moved away from the other till the distance between them becomes 2d. Find the work done by the external force.
View SolutionTwo identical metal plates each having surface area A, having charges q1andq2, are placed facing each other at a separation d. Find the charge appearing on
surface (1),(2),(3), and (4). Assume the size of the plate is much larger than the separation between the plates.View SolutionTwo infinitely large sheets having charge densities σ1andσ2 respectively (σ1>σ2) are placed near each other separated by distance 'd'. A small charge 'q' is placed in between two plates such that there is no effect on charge distribution on plates. Now this charge is moved at an angle of 45∘ with the horizontal towards plate having charge density σ2 by distance 'a' (a<<d). Find the work done by electric field in the process.
View SolutionA capacitor given a charge Q0 is conected across a resistor R at t = 0. The separation between the plates changes according to d=d(1+t)(0≤t<1) Find the variation of charge on capacitor with time.
 View Solution
View SolutionA square of side d, made from a thin insulating plate, is uniformly charged and carries a total charge of Q. A point charge q is placed on the symmetrical normal axis of the square at a distance d/2 from the plate. How large is the force acting on the point charge ?
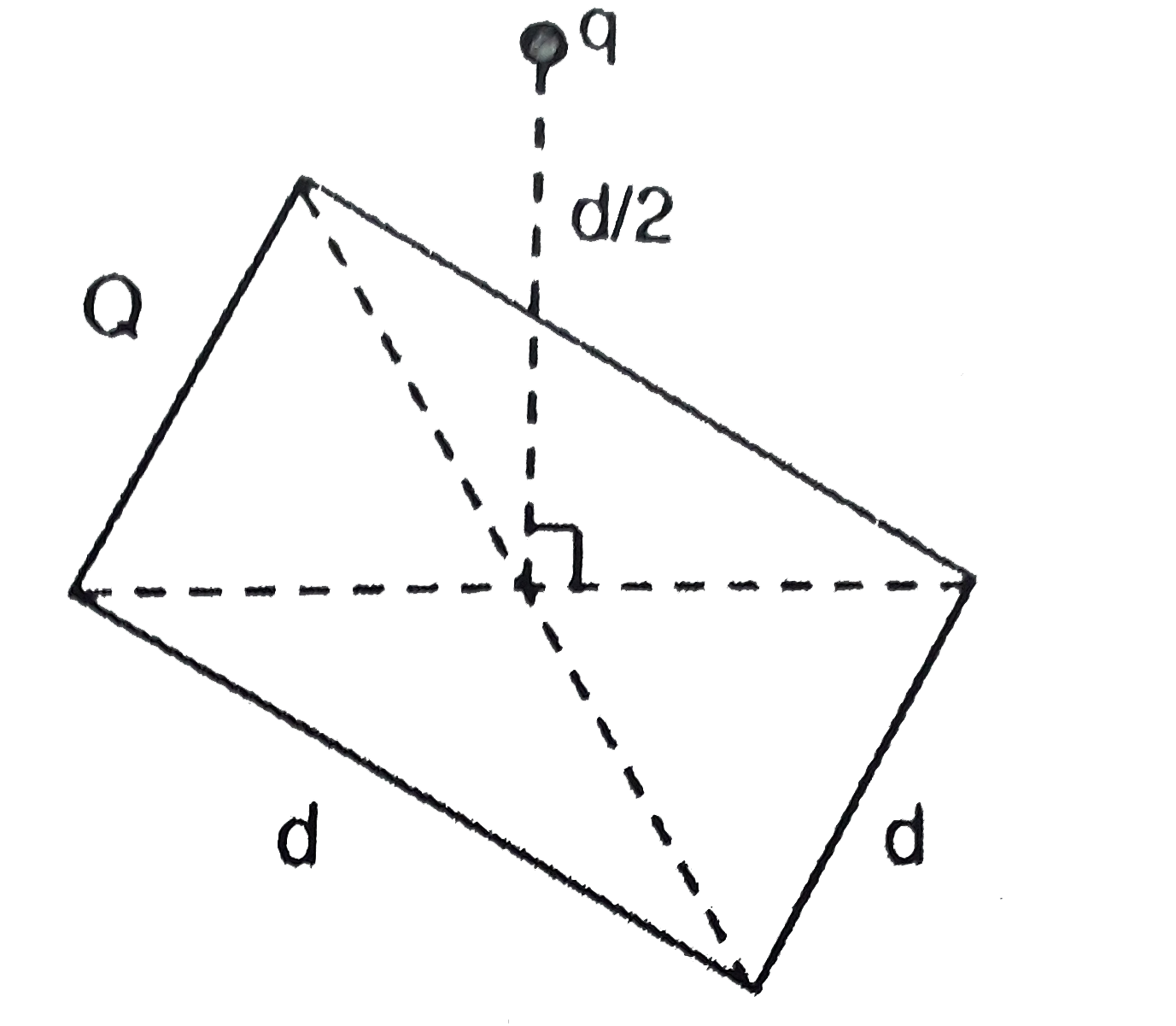 View Solution
View SolutionA parallel plate vacuum capacitor with plate area A and separation x has charges +Q and −Q on its plates. The capacitor is disconnected from the source of charge, so the charge on each plate remains fixed.
(a) What is the total energy stored in the capacitor?
(b) The plates are pulled apart an additional distance dx. What is the change in the stored energy?
(c) If F is the force with which the plates attract each other, then the change in the stored energy must equal the work dW=Fdx done in pulling the plates apart. Find an expression for F.
(d) Explain why F is not equal to QE, where E is the electric field between the plates.View SolutionCalculate the force required to take away a flat circular plate of radius 0.02m from the surface of water. The surface tension of water is 0.07Nm−1
View SolutionCharges 2q and −3q are given to two identical metal plates of area of cross section A. the distance between the plates is d. Find the capacitance and potential difference between the plates.
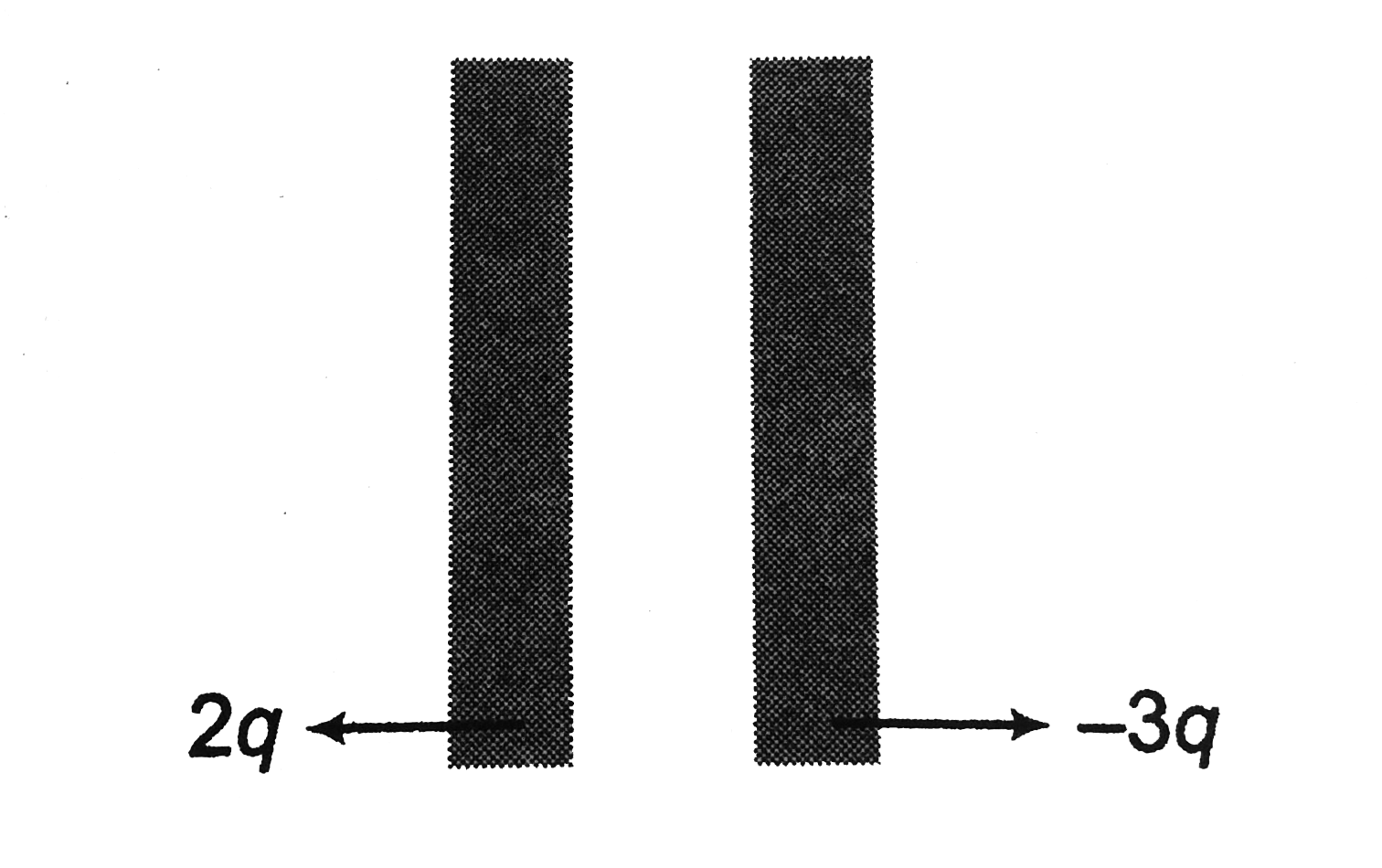 View Solution
View Solution

