Consider one mole of perfect gas in a cylinder of unit cross section with a piston attached as shown in figure. A spring (spring constant k) is attached (unstretched length L ) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of value from V0 to V1.
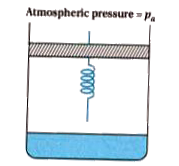
(a) What is the initial pressure of the system ?
(b) What is the final pressure of the system ?
(c) Using the first law of thermodynamics, write down a relation between Q, Pa, V, V0 and k.Solution in Gujrati
(a) Initially system is in equilibrium hence pressure on piston will be the atmospheric pressure.
∴Pi=Pa…(1)
(b)On supply of heat, volume of gas increases from V0 to V1
∴ So increase in volume A×x=V1−V0
(A=area of cross section of cylinder)
If displacement of piston is x then volume increase in cylinder = Area of base x height = A×x
∴A×x=ΔV=V1−V0 (A=Area of cross section of cylinder)
∴x=V1−V0...(2) [∵ A=1 unit]
⇒ The force on piston by spring ,
F=kx
∴F=k(V1−V0)....(3)
∴ Final pressure on the system ,
Pf=Pi+FA
∴Pf=Pa+k(V1−V0)...(4)
[∵ A=1 unit and from equ. (1) and (3)]
It is the final pressure on the gas.
(c) If the final temperature of gas is T, because the walls of cylinder are insulated then increase in internal energy,
ΔU=CVΔT [ ∵μ=1 mole]
∴ΔU=CV(T−T0)..(5)
⇒ Equation of gas at final state,
PfVf=RT
∴T=PfVlR[∵Vf=V1]
∴T=[Pa+k(V1−V0)R]V1
⇒ Volume of gas increased so work done by gas
ΔW=PaΔV + increase in potential energy of spring
∴ΔW=Pa(V1−V0)+12kx2
=P0(V1−V0)+12k(V1−V0)2 ...(6)
From first law of thermodynamics ,
ΔQ=ΔU+ΔW
∴ΔQ=CV(T−T0)+Pa(V1−V0)+12k(V1−V0)2 (From equation (5) and (6) is required relation.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - THERMODYANMICS EXERCISE - Section-E MCQs42videos
THERMODYANMICS
- BOOK - KUMAR PRAKASHANCHAPTER - THERMODYANMICS EXERCISE - Section-F Questions from Module20videos
THERMODYANMICS
- BOOK - KUMAR PRAKASHANCHAPTER - THERMODYANMICS EXERCISE - Section-D Ncert Exemplar Solution (Short Answer )6videos
THERMODYANMICS
- BOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks1videos
THERMAL PROPERTIES OF MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - UNITS AND MEASUREMENTEXERCISE - Section -F (Questions from Module )20videos
UNITS AND MEASUREMENT
Similar Questions
Heat absorbed by the gas undergo a cylic process along closed path in one complete cycle as shown in figure will be _____ J.
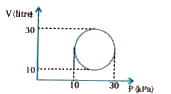 04:34View Solution
04:34View SolutionIn a thermodynamics process which one of the following statement is not true ?
03:54View SolutionConsider a Carnot's cycle operating between T1 = 500 K and T2 = 300 K producing 1 kJ of mechanical work per cycle. Find the heat transferred to the engine by the reservoirs.
03:06View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
08:12View SolutionIf the error in measurement of radius of a shpere is 2% then the error in determination of volume of the sphere will be …………
02:50View SolutionAn ideal monatonic gas is confined in a cylinder by a spring-loaded piston of cross section 8.0×10−3m2.initially the gas is at 300K and occupies a volume of 2.4×10−3m−3 and the sprinng is in its relaxed state. The gas is heated by a small heater until the piston moves out slowly by 0.1m. Calculate the final tenoerature of the gas. The force constant if the spring is 8000Nm−1,and the atmospheric pressure is 1.0×105Nm−2.Htecyl∈derandtheπs→narethermally∈sylated.Theπs→nandthespr∈garemass≤ssandthereisnoictionbetweentheπs→nandthecyl∈der.Neg≤ctanyheat−lossthroughthe≤adwiresoftheheater.Theheat∩acityoftheheatercoilis¬ligib≤.
 02:32View Solution
02:32View SolutionIn the arrangement shown in Fig. gas is thermally insulated. An ideal gas is filled in the cylinder having pressure P_(0) (gt atmospheric pressure P_(0) ). The spring of force constant K is initially unstretched. The piston of mass m and area S is frictionless. In equilibrium, the piston rises up by distance x_(0) , then
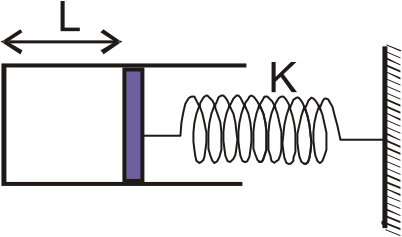
05:04View SolutionA fixed container is fitted with a piston which is attached to a spring of spring constant k. The other and of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an dideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotaional kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
 View Solution
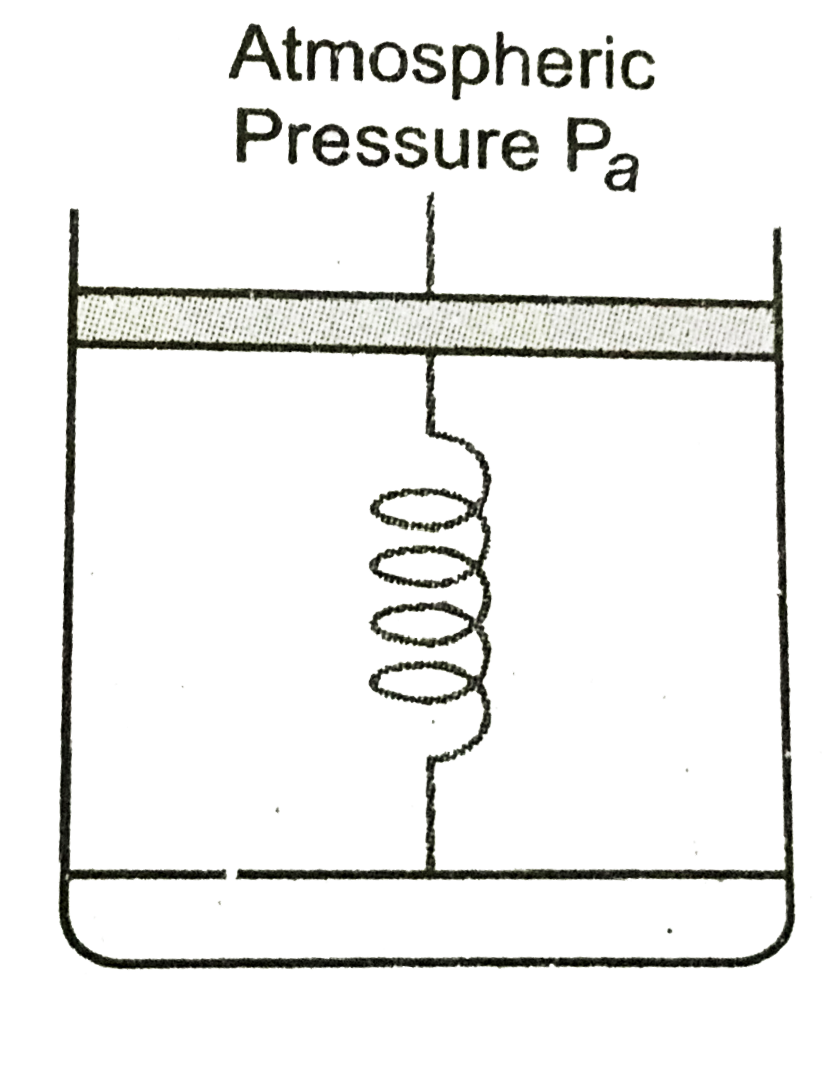
View SolutionConsider one mole of a perfect gas in a cyclinder of unit cross section with a piston attached, (figure) A spring (spring constant K) is attached (unstretched length L) to the piston and the bottom of the cylinder. Initially, the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from V0toV.
(a) What is the initial pressure of the system?
(b) What is the final pressure of the system?
(c) Using the first law of thermodynamics, write down a relation between Q,Pa,V,V0 and K.
 10:09View Solution
10:09View SolutionA gas fills the right portion of a horizontal cylinder whose radius is 5.00 cm . The initial pressure of the gas is 101 kPa . A frictionless movable piston separates the gas from the left portion of the cylinder, which is evacuated and contains an ideal spring, as the drawing shows. The piston is initially unstrained, and the length of the gas-filled portion is 20.0 cm . Wheen the pin is removed and the gas is allowed to expand, the length of the gas-filled chamber doubles when it finally reaches equilibrium. The initial and final temperatures are equal. Determine the spring constant of the spring.
08:54View SolutionIn the equilibrium conditions shown in the figure all the springs have unstretched length l
View SolutionConsider one mole of perfect gas on a cylinder of units cross-section with a piston attched (figure). A spring (spring constant K ) is attched (unstrecthed lengthL ) to the piston and to the bottom of the cylinder . Inditially the spring is unstrecthed and the gas is in equailibrium. A certain amount of heat Q is supplied to the gas causing an increase of value from V0 to V1.
(a) What is the initial pressure of the system ?
(b) What is the final pressure of the system?
(c) Using the first law of thermodynamic, write down a relation between Q,pa,V,V0 and K.
 View Solution
View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless spring loaded with a frictionless piston of negligible mass and of cross-sectional area 4 xx 10^(-3) m^2 . The springis initially in its relaxed state. Now the gas is heated by a heater for some time. During this time the gas expands and does 50 J of work in moving the piston through a distance of 0.1 m. The temperature of the gas increases by 50 K. Calculate the spring constant and the heat supplied by the heater.
10:12View SolutionConsider one mole of perfect gas on a cylinder of units cross-section with a piston attached (figure). A spring (spring constant K ) is attached ( unstretched length L ) to the piston and to the bottom of the cylinder . Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of value from V_(0) to V_(1) . (a) What is the initial pressure of the system ? (b) What is the final pressure of the system? (c) Using the first law of thermodynamic, write down a relation between Q, p_(a),V,V_(0) and K.
View Solution2.00 mole of a monatomic ideal gas (U=1.5nRT) is enclosed in an adiabatic, fixed , vertical cylinder fitted with a smooth, light adiabatic piston. The piston is connected to a vertical spring of spring constant 200Nm−1 as shown in .the area of cross section of the cylinder is 20.0cm2. initially, the spring is at its natural length and the temperature of the gas is 300K at its natural length. the atmosphere pressure is 100 kPa. the gas is heated slowly for some time by means of an electric heater so as to move the position up through 10 cm. find (a) the work done by the gas (b) the final temperature of the gas and (c ) the heat supplied by the heater.
 View Solution
View Solution

