Consider the situation of the previous problem, if the mirror reflects only 64% of the light energy falling on it, what will be the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen ?
The correct Answer is:A
To solve the problem, we need to determine the ratio of the maximum intensity (I_max) to the minimum intensity (I_min) in the interference pattern when a mirror reflects only 64% of the light energy falling on it.
1. Understanding the Reflection Percentage:
- The mirror reflects 64% of the light energy. This means that the intensity of the reflected light (I1) is 64% of the incident intensity (I0).
- Therefore, we can express this as:
I1=0.64I0
- The intensity of the light that is not reflected (I2) is then:
I2=I0−I1=I0−0.64I0=0.36I0
2. Finding the Ratio of Intensities:
- The ratio of the intensities I1 to I2 can be written as:
I1I2=0.64I00.36I0=0.640.36
- Simplifying this gives:
I1I2=6436=169
3. Calculating the Amplitude Ratio:
- Since intensity is proportional to the square of the amplitude (R), we have:
R21R22=169
- Taking the square root gives:
R1R2=√169=43
4. Finding Maximum and Minimum Intensities:
- The maximum intensity (I_max) in the interference pattern is given by:
Imax=(R1+R2)2
- The minimum intensity (I_min) is given by:
Imin=(R1−R2)2
5. Calculating I_max and I_min:
- Let R1=4k and R2=3k for some constant k.
- Then:
Imax=(4k+3k)2=(7k)2=49k2
Imin=(4k−3k)2=(k)2=k2
6. Finding the Ratio of Maximum to Minimum Intensity:
- The ratio of maximum to minimum intensity is:
ImaxImin=49k2k2=49
Final Answer:
The ratio of the maximum to the minimum intensity in the interference pattern is 49:1.
- The mirror reflects 64% of the light energy. This means that the intensity of the reflected light (I1) is 64% of the incident intensity (I0).
- Therefore, we can express this as:
I1=0.64I0
- The intensity of the light that is not reflected (I2) is then:
I2=I0−I1=I0−0.64I0=0.36I0
- The ratio of the intensities I1 to I2 can be written as:
I1I2=0.64I00.36I0=0.640.36
- Simplifying this gives:
I1I2=6436=169
- Since intensity is proportional to the square of the amplitude (R), we have:
R21R22=169
- Taking the square root gives:
R1R2=√169=43
- The maximum intensity (I_max) in the interference pattern is given by:
Imax=(R1+R2)2
- The minimum intensity (I_min) is given by:
Imin=(R1−R2)2
- Let R1=4k and R2=3k for some constant k.
- Then:
Imax=(4k+3k)2=(7k)2=49k2
Imin=(4k−3k)2=(k)2=k2
- The ratio of maximum to minimum intensity is:
ImaxImin=49k2k2=49
The ratio of the maximum to the minimum intensity in the interference pattern is 49:1.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -210videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
Similar Questions
A long horizontal slit is placed 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and the after reflection is seen on a screen 1 m away from the slit. If the mirror reflects only 64% of the light falling on it, the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen is
View SolutionTwo sources with intensity 9 :4 interfere in a medium. Then find the ratio of maximum to the minimum intensity in the interference pattern.
View Solution
Knowledge Check
- Question 1 - Select One
The intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
A2:1B34:1C9:1D8:1
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a YDSE. The paper transimits 4/9 of the light energy falling on it.
a. Find the ratio of maximum intensity to the minimum intensity in interference pattern.
b. How many fringes will cross through the center if an indentical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.View Solution_E01_107_Q01.png)
A narrow monochromatic beam of light of intensity I is incident on a galss plate as shown in figure. Another identical glass plate is kept close to the first one & parallel to it. Each glass plate reflects 25% of the light incident on it % transmits the remaining find the ratio of the minimum & the maximum intensities in the interference pattern formed by the two beams obtained after one reflection at each plate.View SolutionThe intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
View SolutionThe width of one of the two slits in a Young's double slit experiment is double of the other slit. Assuming that the amplitude of the light coming from a slit is proportional to the slit width, find the ratio of the maximum to the minimum intensity in the interference pattern.
View SolutionThe width of one of the two slits in a Young's double slit experiment is double of the other slit. Assuming that the amplitude of the light coming from a slit is proportional to the slit width, find the ratio of the maximum to the minimum intensity in the interference pattern.
View SolutionA transparent glass plate of thickness 0.5 mm and refractive index 1.5 is placed infront of one of the slits in a double slit experiment. If the wavelength of light used is 6000A∘, the ratio of maximum to minimum intensity in the interference pattern is 25/4. Then the ratio of light intensity transmitted to incident on thin transparent glass plate is
View SolutionA point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
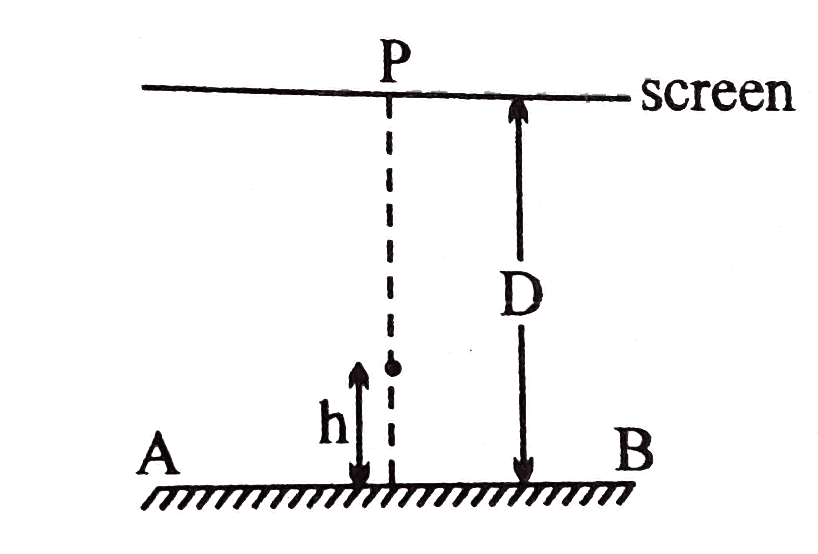
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.View Solution

