Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when <AOC=90∘.
To solve the problem, we need to find the current in the rod OA when the angle AOC is 90 degrees. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a circular loop with resistance R uniformly distributed along its length. The rod OA is rotating with a uniform angular speed ω and is connected to point O and C, where the wire OC has zero resistance.
Step 2: Identify the Resistance in the Loop
When the angle AOC is 90 degrees, the rod OA divides the circular loop into two parts:
- The segment from A to C (which is one-fourth of the loop).
- The remaining segment from C to O (which is three-fourths of the loop).
Since the resistance R is uniformly distributed, the resistance of the segment from A to C is:
RAC=R4
And the resistance of the segment from C to O is:
RCO=3R4
Step 3: Calculate the Total Resistance
The two segments are in parallel when considering the current flow through the loop. The equivalent resistance R′ of the two segments can be calculated using the formula for resistors in parallel:
1R′=1RAC+1RCO=1R4+13R4=4R+43R
Finding a common denominator (which is 3R):
1R′=123R+43R=163R
Thus, the equivalent resistance R′ is:
R′=3R16
Step 4: Calculate the Induced EMF
The induced EMF E in the loop can be calculated using the formula:
E=B⋅L⋅V
Here, L is the length of the rod (which is the radius a), and V is the linear velocity of the rod, given by V=aω. Therefore, the induced EMF becomes:
E=B⋅a⋅(aω)=Ba2ω
Step 5: Calculate the Current
Now we can find the current I flowing through the rod using Ohm's law:
I=ER′
Substituting the values we have:
I=Ba2ω3R16=16Ba2ω3R
Final Answer
The current in the rod OA when the angle AOC is 90 degrees is:
I=16Ba2ω3R
We have a circular loop with resistance R uniformly distributed along its length. The rod OA is rotating with a uniform angular speed ω and is connected to point O and C, where the wire OC has zero resistance.
When the angle AOC is 90 degrees, the rod OA divides the circular loop into two parts:
- The segment from A to C (which is one-fourth of the loop).
- The remaining segment from C to O (which is three-fourths of the loop).
RAC=R4
And the resistance of the segment from C to O is:
RCO=3R4
The two segments are in parallel when considering the current flow through the loop. The equivalent resistance R′ of the two segments can be calculated using the formula for resistors in parallel:
1R′=1RAC+1RCO=1R4+13R4=4R+43R
Finding a common denominator (which is 3R):
1R′=123R+43R=163R
Thus, the equivalent resistance R′ is:
R′=3R16
The induced EMF E in the loop can be calculated using the formula:
E=B⋅L⋅V
Here, L is the length of the rod (which is the radius a), and V is the linear velocity of the rod, given by V=aω. Therefore, the induced EMF becomes:
E=B⋅a⋅(aω)=Ba2ω
Now we can find the current I flowing through the rod using Ohm's law:
I=ER′
Substituting the values we have:
I=Ba2ω3R16=16Ba2ω3R
The current in the rod OA when the angle AOC is 90 degrees is:
I=16Ba2ω3R
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed (ω) as shown in the figure. Find the current in the rod when −AOC=90∘
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity ω about its end, compute its magnetic moment.
 View Solution
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity ω about its end, compute its magnetic moment.
 View Solution
View SolutionA uniform rod of length l is rotating with constant angular speed ω as shown in figure. Choose the graph which correctly shows the variation of T with x.
_2019_CBT7_E01_017_Q01.png) View Solution
View SolutionShows a conducting circular loop radius a placed in a uniform, perpendicular magnetic field B. A metal rod OA is pivoted at the centre O of the loop. The other A of the rod touches the loop. The rod OA and the loop are resistanceless but a resistor having a resistance R is connected between O and a fixed point C on the loop . the rod OA is made to rotate anticlockwise at a small but uniform angular speed omega by an external force. Find (a) the current in the resistance R and (b) the torque of the external force needed ot keep the rod rotating with the constant angular velocity omega.
 View Solution
View SolutionConsider a variation of the previous problem. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistance but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity (ω) in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it.
Find the magnitude of this force when the rod makes an angle (θ) with the vertical.View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 View Solution
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 View Solution
View SolutionA square wire of resistance 1.3Ω and side 1cm is moving in uniform magnetic field B=1T with speed 1cm/sec as shown in figure then the current in loop is :
_2019_CBT7_E01_024_Q01.png) View Solution
View SolutionA rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
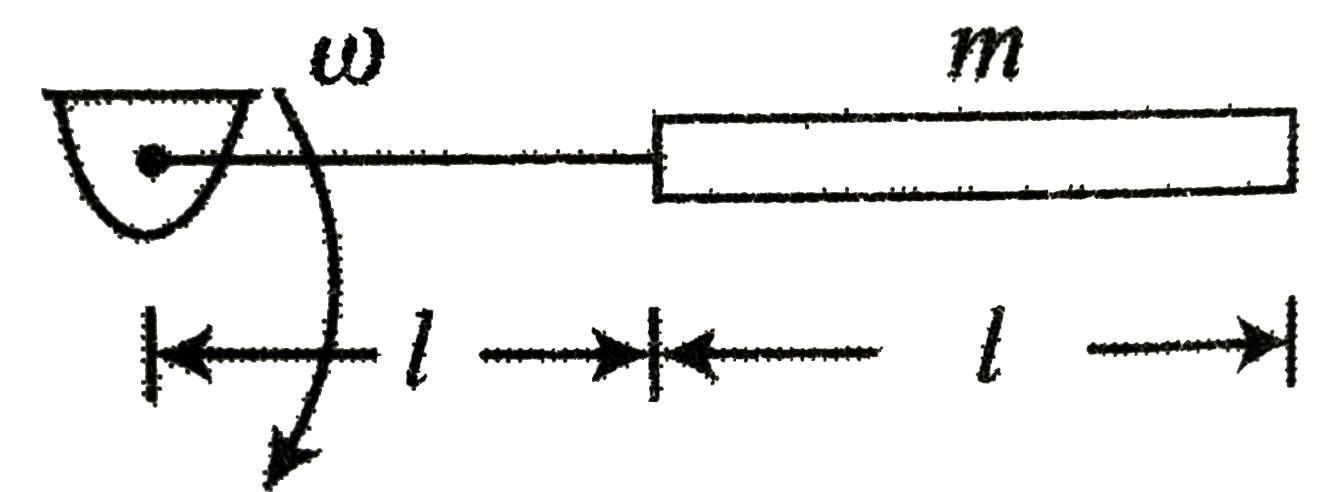
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.View Solution

