Consider two conductors. One of them has a capacity of 2 units and the capacity of the other is unknown. They are charged until their potential are 4 and 5 units respectively. The two conductors are now connected by a wire when their common potential is found to be 4.6 units. Then the unknown capacity has the value (in the same units as above)
6
5
4
3
The correct Answer is:D
To solve the problem, we need to apply the principle of conservation of charge. Here's a step-by-step solution:
Step 1: Define the known values
Let:
- C1=2 units (the capacitance of the first conductor)
- V1=4 units (the potential of the first conductor)
- V2=5 units (the potential of the second conductor)
- C2=x units (the capacitance of the second conductor, which we need to find)
- The common potential after connecting the conductors is Vf=4.6 units.
Step 2: Calculate the initial charges on each conductor
The charge on a capacitor is given by the formula:
Q=C×V
Thus, the initial charges on the conductors are:
- Charge on the first conductor:
Q1=C1×V1=2×4=8 units
- Charge on the second conductor:
Q2=C2×V2=x×5
Step 3: Write the conservation of charge equation
According to the conservation of charge, the total initial charge before connecting the conductors is equal to the total charge after they are connected:
Qinitial=Qfinal
Thus, we can write:
Q1+Q2=(C1+C2)×Vf
Substituting the values we have:
8+5x=(2+x)×4.6
Step 4: Expand and simplify the equation
Expanding the right-hand side:
8+5x=2×4.6+x×4.6
8+5x=9.2+4.6x
Step 5: Rearranging the equation
Now, we will rearrange the equation to isolate x:
8+5x−4.6x=9.2
8+0.4x=9.2
Subtracting 8 from both sides:
0.4x=1.2
Step 6: Solve for x
Now, divide both sides by 0.4:
x=1.20.4=3 units
Conclusion
The unknown capacitance C2 is 3 units.
---
Let:
- C1=2 units (the capacitance of the first conductor)
- V1=4 units (the potential of the first conductor)
- V2=5 units (the potential of the second conductor)
- C2=x units (the capacitance of the second conductor, which we need to find)
- The common potential after connecting the conductors is Vf=4.6 units.
The charge on a capacitor is given by the formula:
Q=C×V
- Charge on the first conductor:
Q1=C1×V1=2×4=8 units
- Charge on the second conductor:
Q2=C2×V2=x×5
According to the conservation of charge, the total initial charge before connecting the conductors is equal to the total charge after they are connected:
Qinitial=Qfinal
Thus, we can write:
Q1+Q2=(C1+C2)×Vf
Substituting the values we have:
8+5x=(2+x)×4.6
Expanding the right-hand side:
8+5x=2×4.6+x×4.6
8+5x=9.2+4.6x
Now, we will rearrange the equation to isolate x:
8+5x−4.6x=9.2
8+0.4x=9.2
Subtracting 8 from both sides:
0.4x=1.2
Now, divide both sides by 0.4:
x=1.20.4=3 units
The unknown capacitance C2 is 3 units.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two parallel plate condensers of capacity 20mF and 30mF are charged to the potentials of 30 V and 20 V respectively. If likely charged plates are connected together then the common potential difference be
View SolutionTwo capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
View Solution
Knowledge Check
Two identical capacitors, have the same capacitance C. One of them is charged to potential V1 and the other V2. The negative ends of the capacitors are connected together. When the poistive ends are also connected, the decrease in energy of the combined system is
A14C(V21−V22)B14C(V21+V22)C14C(V1−V2)2D14C(V1+V2)2
The capacities of two conductors are C1 and C2 and their respectively potentials are V1 and V2. If they are connected by a thin wire, then the loss of energy will be given by
View SolutionTwo capacitors having capacitances C1 and C2 are charged with 120 V and 200 V batteries respectively. When they are connected in parallel now, it is found that the potential on each one of them is zero. Then,
View SolutionTwo capacitors having capacitances C1 and C2 are charged with 120 V and 200 V batteries respectively. When they are connected in parallel now, it is found that the potential on each one of them is zero. Then,
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then
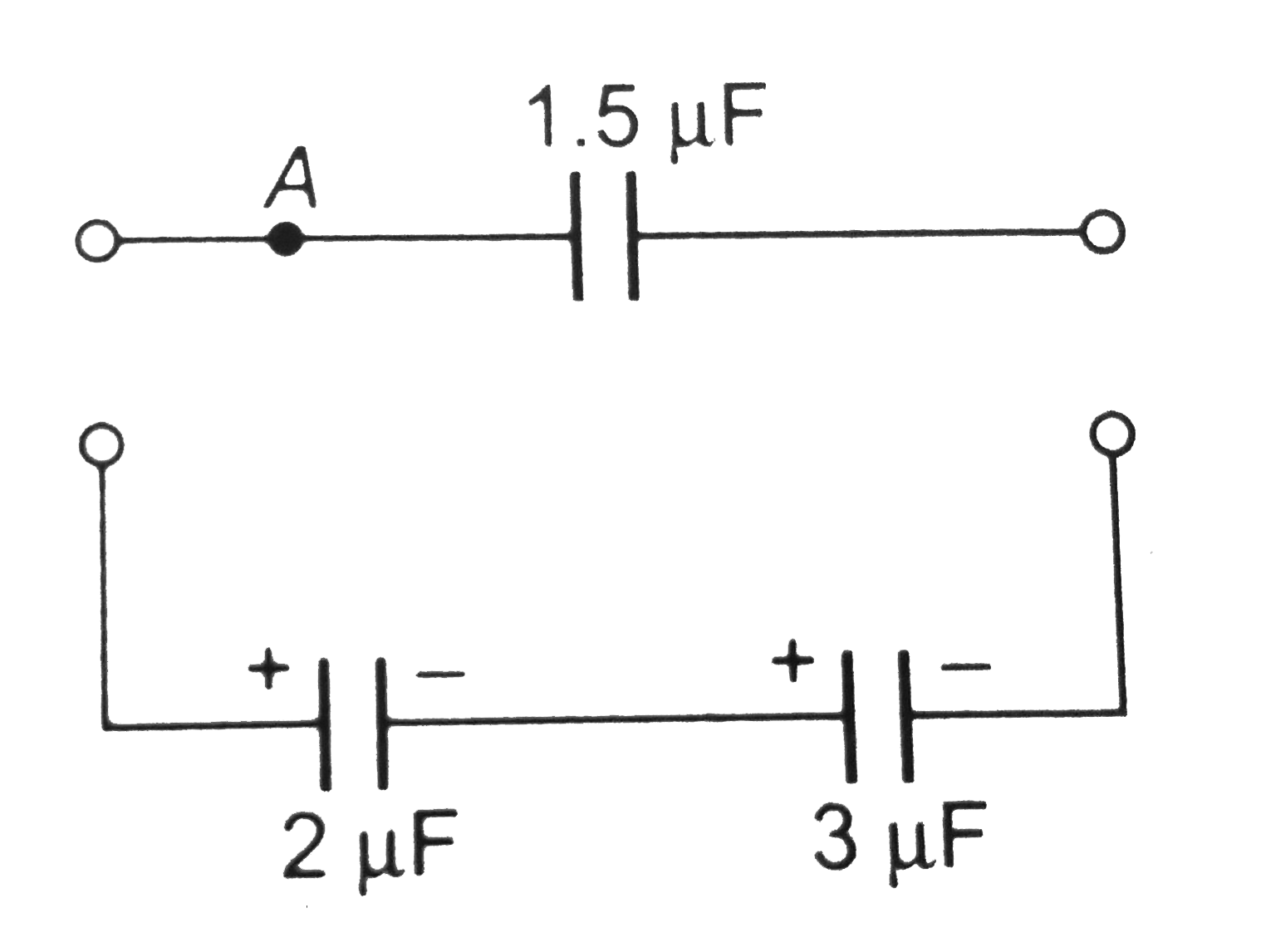
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then

View SolutionTwo spheres A and B of radius 4 cm and 6 cm are given charges of 80μCand40μC, respectively. If they are connected by a fine wire, then the amount of charge flowing from one to the other is
View SolutionTwo identical capacitors, have the same capacitance C. One of them is charged to potential V1 and the other V2. The negative ends of the capacitors are connected together. When the poistive ends are also connected, the decrease in energy of the combined system is
View Solution
