Consider two configurations of a system of three particles of masses m, 2m and 3m. The work done by gravity in changing the configuration of the system from figure (i) to figure (ii) is 
zero
6Gm2a{1+1√2}
6Gm2a{1−1√2}
6Gm2a{2−1√2}
The correct Answer is:C
W=−ΔU=Ui−Uf
=−Gmma[{(1)(2)1+(1)(3)1+(2)(3)√2}]
−{(1×2)1+(1×3)1+(2×3)1}]
=6GM2a(1−1√2)
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective
19 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
Knowledge Check
The velocity (in m/s) of centre of mass of the system as shown in the figure is :
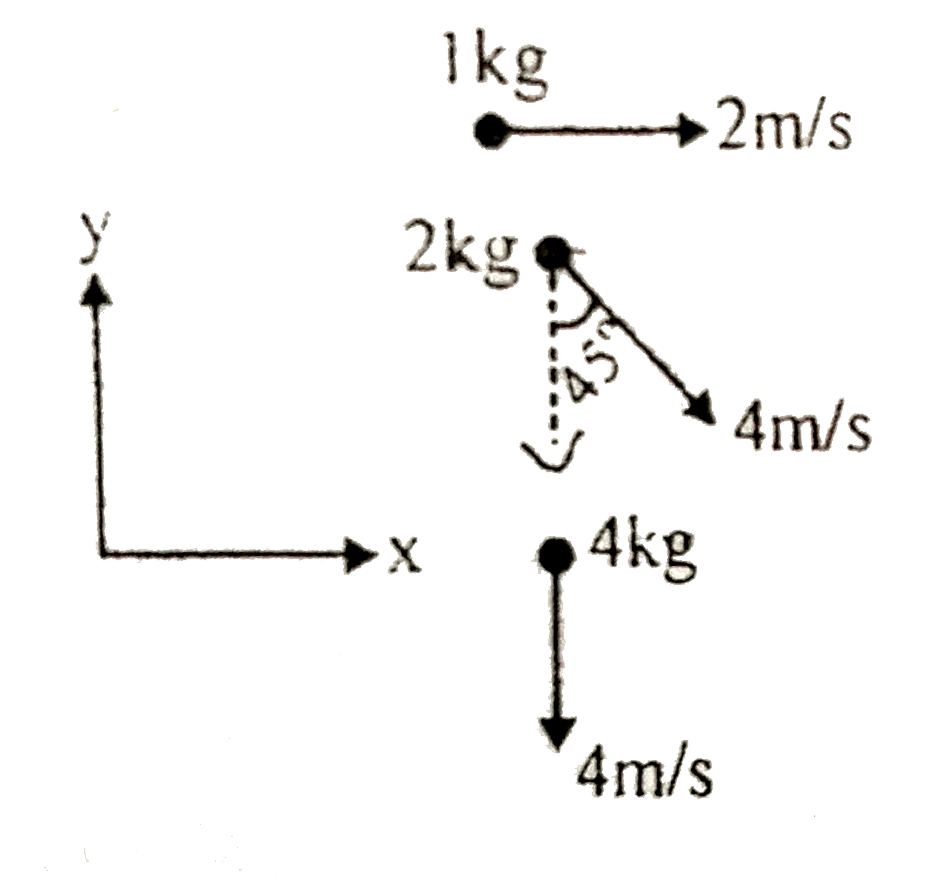 A2[1+4√2]ˆi+8[1√2+2]ˆj7B2[1+4√2]ˆi+8[1√2−2]ˆj7C2[1+4√2]ˆi−8[1√2+2]ˆj7D8[1√2−2]ˆi+2[1+4√2ˆj]7
A2[1+4√2]ˆi+8[1√2+2]ˆj7B2[1+4√2]ˆi+8[1√2−2]ˆj7C2[1+4√2]ˆi−8[1√2+2]ˆj7D8[1√2−2]ˆi+2[1+4√2ˆj]7Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
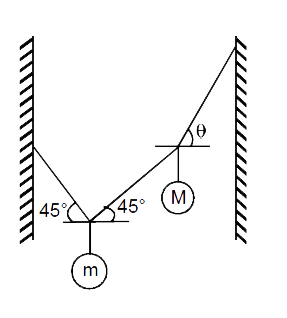 Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mM
Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mMTwo point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)
Four particles of masses m, m, 2m and 2m are placed at the four corners of square of side a. Find the centre of mass of the system.
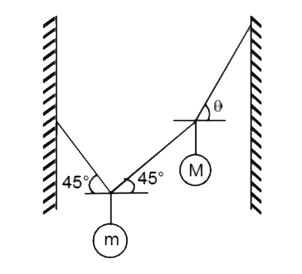
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibruim, then
View SolutionThree particles of masses 1 kg, 2 kg and 3 kg are at distance 1 m, 2 m and 3 m from the axis of rotation. The moment of intertia of the system is
View SolutionTwo point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
View SolutionThree particles, two with mass m and one with mass M, might be arranged in any of Rank the configuration according of the gravitational force on M, least to greatest.

View Solution

 ,
,