Consider two identical charges placed a distance 2d apart on the x-axis.The equilibrium of a positive test charge placed at the point O midway between them may be
(i) neutral
(ii) stable for displacement along the x-axis
(iii) stable for displacement along the y-axis
(iv) unstable for displacement along the x-axis
stable for displacements along the x-axis
neutral
unstable for displacement along the y-axis.
stable for displacements along the y-axis
The correct Answer is:A, C
To analyze the equilibrium of a positive test charge placed at point O, which is midway between two identical charges on the x-axis, we can follow these steps:
Step 1: Understand the Setup
We have two identical positive charges, each denoted as Q, placed a distance of 2d apart on the x-axis. The test charge q0 is placed at point O, which is located at the midpoint between the two charges. Therefore, the distance from point O to each charge is d.
Step 2: Analyze Forces in the x-direction
When the test charge q0 is at point O and is displaced slightly to the left or right along the x-axis:
- If displaced to the left, the distance to the left charge decreases while the distance to the right charge increases.
- The electrostatic force from the left charge (let's call it FL) increases because it is inversely proportional to the square of the distance, while the force from the right charge (let's call it FR) decreases.
Since FL becomes greater than FR when displaced to the left, the net force will push the test charge back towards point O. This indicates that the equilibrium is stable for displacements along the x-axis.
Step 3: Analyze Forces in the y-direction
Now, consider displacing the test charge q0 in the y-direction:
- The forces from both charges will have horizontal components that cancel each other out due to symmetry, but they will have vertical components that will add up.
- The net force will act in the direction of the displacement, meaning if the charge is displaced upward, it will continue to move upward, and if displaced downward, it will continue to move downward.
This indicates that the equilibrium is unstable for displacements along the y-axis.
Step 4: Conclusion
Based on the analysis:
- The equilibrium is stable for displacement along the x-axis.
- The equilibrium is unstable for displacement along the y-axis.
Thus, the correct answer is that the equilibrium of the positive test charge placed at point O is:
- (ii) stable for displacement along the x-axis
- (iv) unstable for displacement along the y-axis
Summary of Answers
- (i) Neutral: Incorrect
- (ii) Stable for displacement along the x-axis: Correct
- (iii) Stable for displacement along the y-axis: Incorrect
- (iv) Unstable for displacement along the x-axis: Incorrect
We have two identical positive charges, each denoted as Q, placed a distance of 2d apart on the x-axis. The test charge q0 is placed at point O, which is located at the midpoint between the two charges. Therefore, the distance from point O to each charge is d.
When the test charge q0 is at point O and is displaced slightly to the left or right along the x-axis:
- If displaced to the left, the distance to the left charge decreases while the distance to the right charge increases.
- The electrostatic force from the left charge (let's call it FL) increases because it is inversely proportional to the square of the distance, while the force from the right charge (let's call it FR) decreases.
Now, consider displacing the test charge q0 in the y-direction:
- The forces from both charges will have horizontal components that cancel each other out due to symmetry, but they will have vertical components that will add up.
- The net force will act in the direction of the displacement, meaning if the charge is displaced upward, it will continue to move upward, and if displaced downward, it will continue to move downward.
Based on the analysis:
- The equilibrium is stable for displacement along the x-axis.
- The equilibrium is unstable for displacement along the y-axis.
- (ii) stable for displacement along the x-axis
- (iv) unstable for displacement along the y-axis
- (i) Neutral: Incorrect
- (ii) Stable for displacement along the x-axis: Correct
- (iii) Stable for displacement along the y-axis: Incorrect
- (iv) Unstable for displacement along the x-axis: Incorrect
Similar Questions
Two equal positive point charges 'Q' are fixed at points B (a, 0) and A(-a, 0). Another test charge q0 is also placed at O (0, 0). Show that the equilibrium at 'O' is
(i) Stable for displacement along X-axis
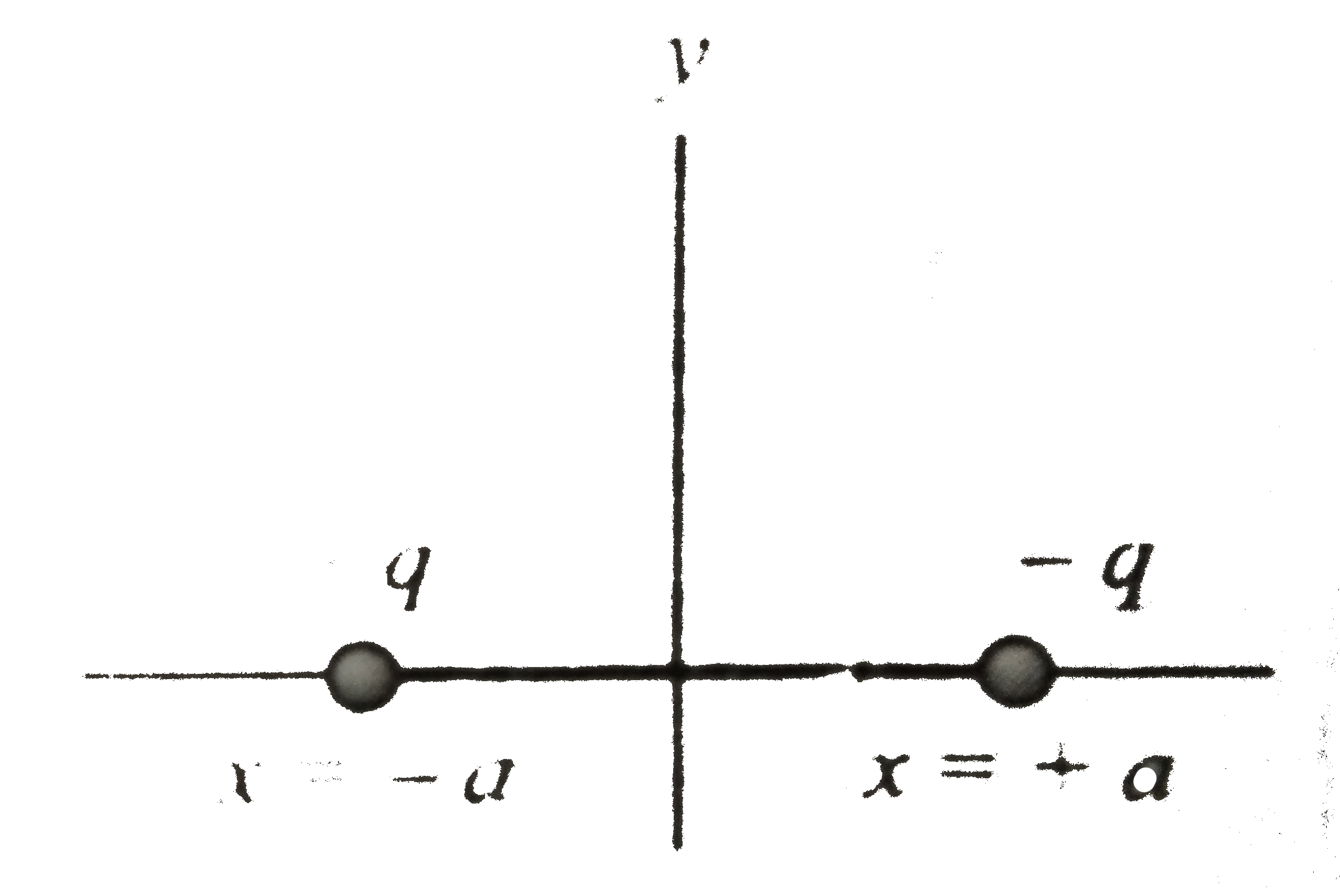
(ii) Unstable for displacement along Y-axis.View SolutionTwo point charge ±q are placed on the axis at x=−a and x=+a, as shown in fig.
(i) Plot the variation of E along the x-axis.
(ii) Plot the variation of E along the y-axis.
 View Solution
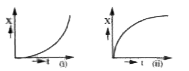
View SolutionFigures (i) and (ii) below show the displacement - time graphs of two particles moving along the x-axis. We can say that
 View Solution
View SolutionAn electric dipole is placed along x-axis with its centre at origin:
View SolutionTwo equal point charges are fixed at x=−a and x=+a on the x-axis. Another point charge Q is placed at the origin. The change in the electrical potential energy of Q, when it is displaced by a small distance x along the x-axis, is approximately proportional to
View SolutionTwo charges, each equal to q, aer kept at x=−a and x=a on the x-axis. A particle of mass m and charge q0=q2 is placed at the origin. If charge q0 is given a small displacement (ylt lt a) along the y-axis, the net force acting on the particle is proportional to
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that at the three charges are in equilibrium. Then
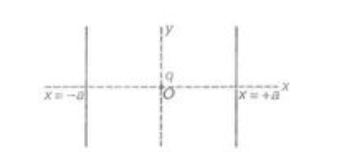
View SolutionTwo identical infinite positive line changes are places into the lines x=±a in the x=y plane. A positive point charge placed at origin is restricted to move along x-axis its equilibrium is
 View Solution
View SolutionTwo identical positive charges are placed at x=−a and x=a. The correct variation of potential V along the x-axis is given by
View SolutionThe displacement of a particle along the x- axis it given by x=asin2ωt The motion of the particle corresponds to
View Solution
