Consider two solid uniform spherical objects of the same density ρ. One has radius R and the other has radius 2R. They are in outer space where the gravitational fields from other objects are negligible. If they are arranged with their surface touching, what is the contact force between the objects due to their traditional attraction?
Gπ2R4
12881Gπ2R4ρ2
12881Gπ2
12887π2R2G
The correct Answer is:B
To solve the problem of finding the contact force between two solid uniform spherical objects due to their gravitational attraction, we can follow these steps:
Step 1: Determine the Mass of Each Sphere
1. For the smaller sphere (radius R):
- Volume V1=43πR3
- Mass m1=ρ⋅V1=ρ⋅43πR3
2. For the larger sphere (radius 2R):
- Volume V2=43π(2R)3=43π⋅8R3=323πR3
- Mass m2=ρ⋅V2=ρ⋅323πR3
Step 2: Calculate the Gravitational Force Between the Two Spheres
The gravitational force F between two masses is given by Newton's law of gravitation:
F=Gm1m2r2
where r is the distance between the centers of the two spheres. Since the spheres are touching, the distance r is equal to the sum of their radii:
r=R+2R=3R
Step 3: Substitute the Masses and Distance into the Gravitational Force Equation
Substituting m1 and m2 into the gravitational force equation:
F=G(ρ⋅43πR3)(ρ⋅323πR3)(3R)2
Step 4: Simplify the Expression
1. Calculate the numerator:
F=G⋅ρ2⋅1289π2R69R2
2. Simplify the denominator:
(3R)2=9R2
3. Combine the terms:
F=G⋅ρ2⋅1289π2R69R2=G⋅ρ2⋅128π2R481
Final Result
Thus, the contact force between the two spheres due to their gravitational attraction is:
F=128Gρ2π2R481
---
1. For the smaller sphere (radius R):
- Volume V1=43πR3
- Mass m1=ρ⋅V1=ρ⋅43πR3
- Volume V2=43π(2R)3=43π⋅8R3=323πR3
- Mass m2=ρ⋅V2=ρ⋅323πR3
The gravitational force F between two masses is given by Newton's law of gravitation:
F=Gm1m2r2
where r is the distance between the centers of the two spheres. Since the spheres are touching, the distance r is equal to the sum of their radii:
r=R+2R=3R
Substituting m1 and m2 into the gravitational force equation:
F=G(ρ⋅43πR3)(ρ⋅323πR3)(3R)2
1. Calculate the numerator:
F=G⋅ρ2⋅1289π2R69R2
(3R)2=9R2
F=G⋅ρ2⋅1289π2R69R2=G⋅ρ2⋅128π2R481
Thus, the contact force between the two spheres due to their gravitational attraction is:
F=128Gρ2π2R481
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Two uniform solid spheres of same materical and same radius are touching each other density is 'ρ' then find out gravitational force between them .
View SolutionSpheres of the same material and same radius r are touching each other. Show that gravitational force between them is directly proportional to r4.
View Solution
Knowledge Check
Two metal spheres, one fo radius R and the other of radius 2R, both have same surface charge density s. They are brought in contact and seprated. What will be new surface charge densitites on them ?
A52σ,54σB53σ,56σC35σ,65σD23σ,12σ
Spheres of the same material and same radius r are touching each other. Show that gravitational force between them is directly proportional to r4.
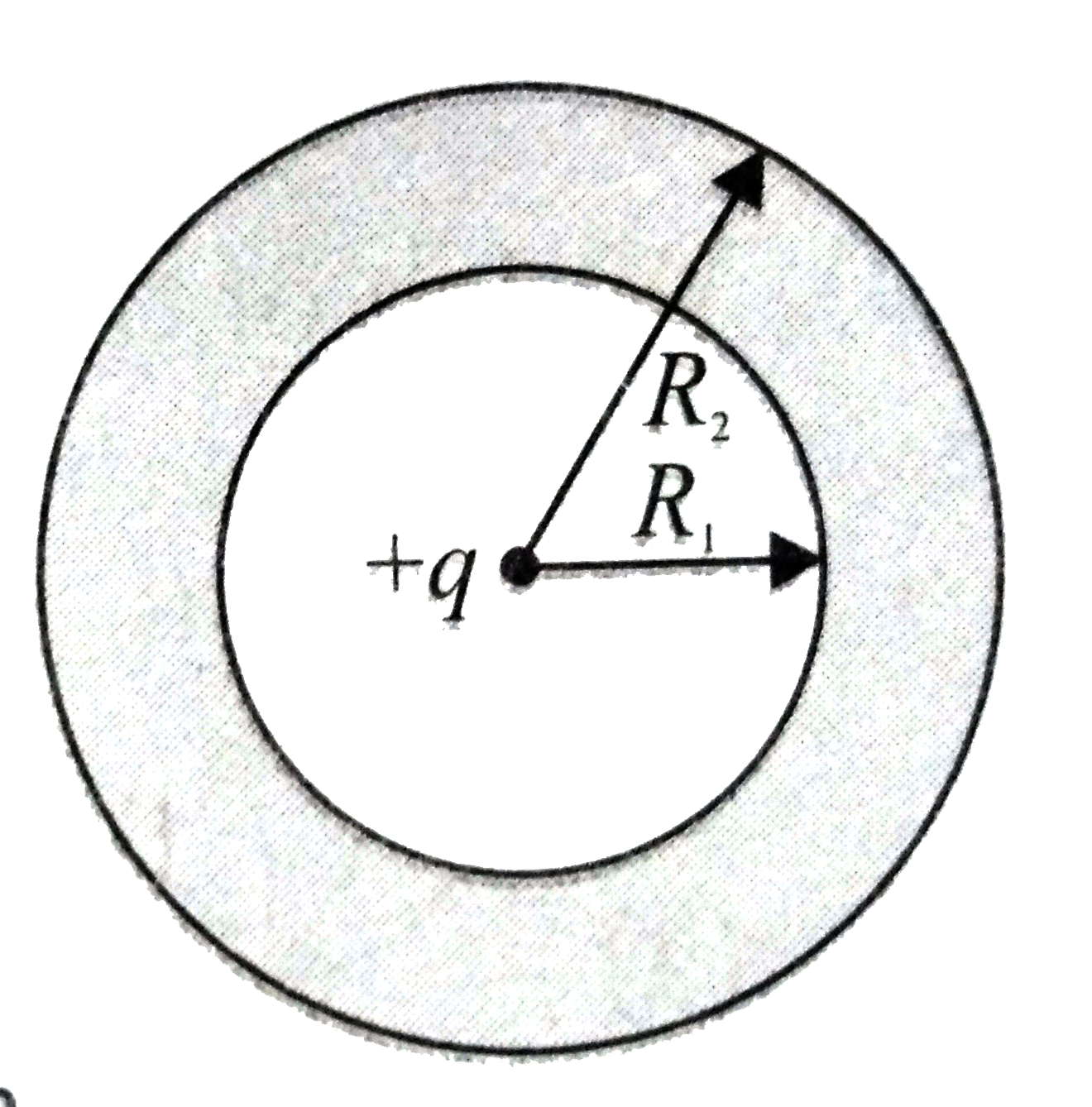
View SolutionA metal spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?
View SolutionTwo metal spheres, one fo radius R and the other of radius 2R, both have same surface charge density s. They are brought in contact and seprated. What will be new surface charge densitites on them ?
View SolutionTwo spheres of the same material and same radius r are touching each other. If the gravitational force of attraction between them is directly proportional to rn, then the value of n is :
View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is
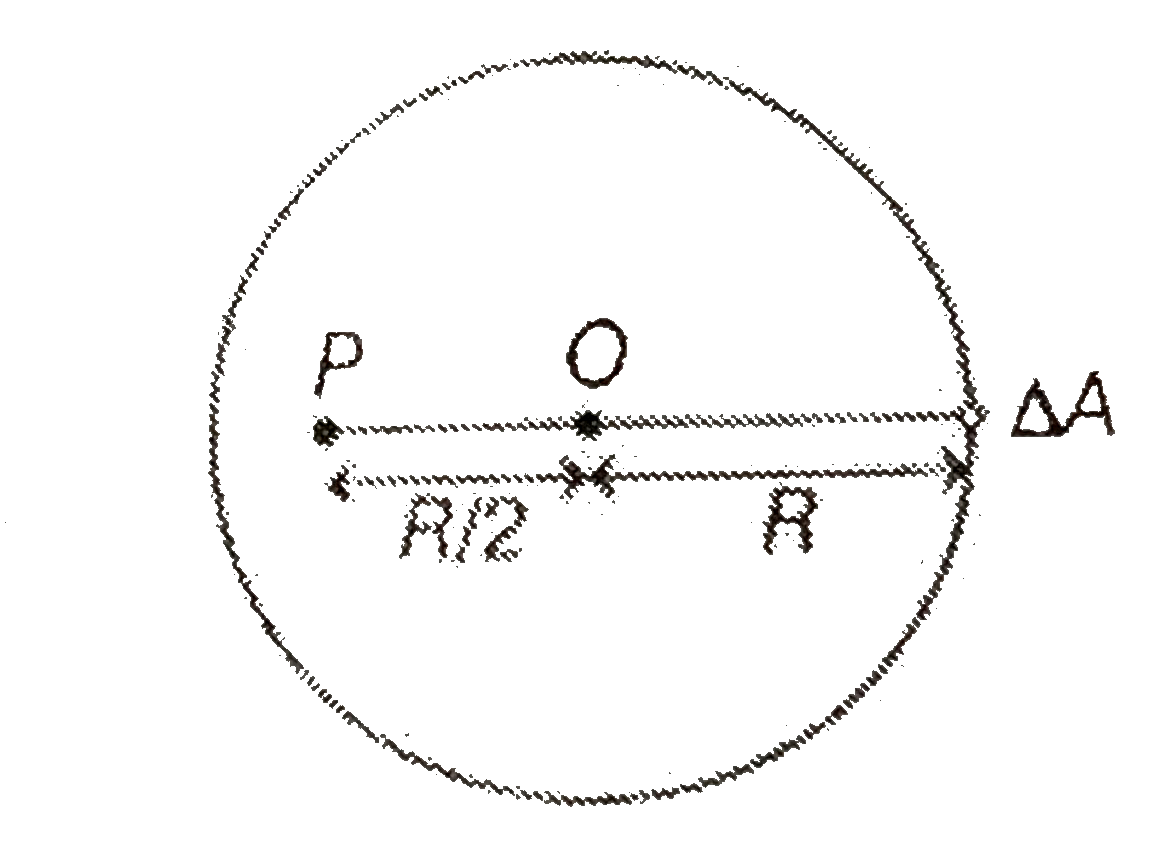
View SolutionA small section of area ΔA is removed from a uniform spherical shell with surface mass density σ and radius R as shown in the figure . Find the magnitude of gravitational field intensity at point P due to the remaining mass .
View SolutionA fixed spherical shell of inner radius R and outer radius 2R has mass M, A particle of mass m is held at rest at a distance 2R from the surface of the body. If the particle is released from that point, with what speed will it hit surface of the spherical body ?
View Solution
