Deduce an expression for the frequency of revolution of a charged particle in a magnetic field and show that it is independent of velocity or energy of the particle.
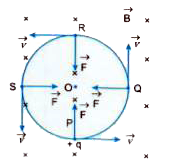
When a charged particle having charge q and moving with a velocity →v enters a uniform magnetic field →B, it experiences a Lorentz force →F=q(→v×→B) whose direction is given by Fleming.s left hand rule. The force is maximum when charged particle is moving perpendicular to the magnetic field. In that case
F=qvBsin90∘=qvB
As the force is acting perpendicular to both →vand→B, it does not change the magnitude of velocity but changes its direction from a straight from a straight line path to a circular path of radius r such that the magnetic force - centripetal force needed.
∴Bqv=mv2r⇒r=mvBq
The time period and frequency of the charged particle in its circular path will be
T=2πrv=2π(mvBq)v=2πmBq, Frequency v=1T=Bq2πm
and angular frequency ω=2πv=qBm.
From this relation it is clear that the time period (as well as frequency) is independent of the velocity (energy) of the charged particle as well as the radius of the circular path.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-II
11 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SELF ASSESSMENT TEST (SECTION A) (MULTIPLE CHOICE QUESTIONS)
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SHORT ANSWER QUESTIONS
41 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
Deduce the expression for the frequency of revolution of a charged particle in a magnetic field and show that this is independent of the velocity or energy of the particle.
View SolutionDeduce the expression for the frequency of revolution of a charged particle in a magnetic field and show that this is independent of the velocity or energy of the particle.
View Solution
Knowledge Check
In a cyclotron, the angular frequency of a charged particle is independent
AMassBSpeedCChargeDMagnetic fieldThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy.
The working of a cyclotron is based on the fact thatAThe force experienced by a charged particles in an electric field is independent of its velocityBThe radius of the circular orbit of a charged particle in a magnetic field increase with increase in its speedCThe frequency of revolution of the particle along the circular path does not depend on its speedDAll of the aboveThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy.
Cyclotron is not suitable for acceleratingAElectronBProtonsCDeutronsDAlpha particles
Show that the frequency of revolution, of a charged particle (in the X-Y plane), in a uniform magnetic field →B(=Bˆk) is independent of its speed.
Which pratical machine makes use of this fact?
What is the frequency of the alternating electric field used in this machine?
View SolutionIn a cyclotron, the angular frequency of a charged particle is independent
View SolutionThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy.
The working of a cyclotron is based on the fact that
View SolutionThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy.
Cyclotron is not suitable for accelerating
View SolutionWrite an expression for the force experienced by the charged particle moving in a uniform magnetic field B. With the help of labeled diagram explain the working of cyclotron. Show that cyclotron frequency does not depend upon the speed of the particle.
View Solution
