Define angular velocity (ω). Derive v=rω .
Angular velocity (ω): Rate of change of angular displacement is called angular velocity.
Relation between linear velocity (v) and angular velocity (ω): Let a particle P is moving on the circumference of a circle of radius .r. with uniform speed v. Let it is initially at the position A, during a small time Δt it goes to a new position say C from B. Angle subtended during this small interval is say dθ

By definition angular velocity, ω=LtΔr→0ΔθΔt=dθdt
But linear velocity v=LtΔt→0BCΔt
When is small arc BC=rdθ⇒v=rdθdt
∴v=r.ω(∵dθdt=ω)
Topper's Solved these Questions
- MODEL PAPER 7BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 7EXERCISE - SECTION -C
3 Videos
- MODEL PAPER 7BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 7EXERCISE - SECTION -C
3 Videos
- MODEL PAPER 6BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 6EXERCISE - SECTION - C
3 Videos
- MODEL PAPER 8BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 8EXERCISE - SECTION - C
3 Videos
Similar Questions
A ody is in pure rotation. The linear speed v of a particle, the distance r of the particle from the axis and the angular velocity ω of the body are related as ω=vr. Thus
View SolutionA body is in pure rotation. The linear speed 'v' of a particle, the distance 'r' of the particle from the axis and the angular velocity ω of the body are related as ω=vr. Thus
View Solution
Knowledge Check
A satellite of mass m revolves revolves round the earth of mass M in a circular orbit of radius r with an angular velocity ω. If the angular velocity is ω/8 then the radius of the orbit will be
A4rB2rC8rDrA sphere is moving on a smooth surface with angular velocity ω and linear velocity v. If collides elastically with another identical sphere B kept at rest. Neglecting friction everywhere, let VA and ωA be linear and angular velocities of sphere A after the impact and let VB and ωB be the corresponding parameters for spehre B. Then
AVA=0,ωA=0BVB=v,ωB=0CVB=0,ωB=ωDωA=0,ωB=ω
A ody is in pure rotation. The linear speed v of a particle, the distance r of the particle from the axis and the angular velocity ω of the body are related as ω=vr. Thus
View SolutionParticles AandB move with constant and equal speeds in a circle as shown in (Fig. 5.164). Find the angular velocity of the particle A with respect to B, if the angular velocity of particle Aw.r.t.O is ω.
 .
.
View SolutionParticles AandB move with constant and equal speeds in a circle as shown in (Fig. 5.164). Find the angular velocity of the particle A with respect to B, if the angular velocity of particle Aw.r.t.O is ω.
 .
.
View SolutionA disc with linear velocity v and angular velocity ω is placed on rough ground. Suppose a and α be the magnitudes of linear and angular acceleration due to friction.
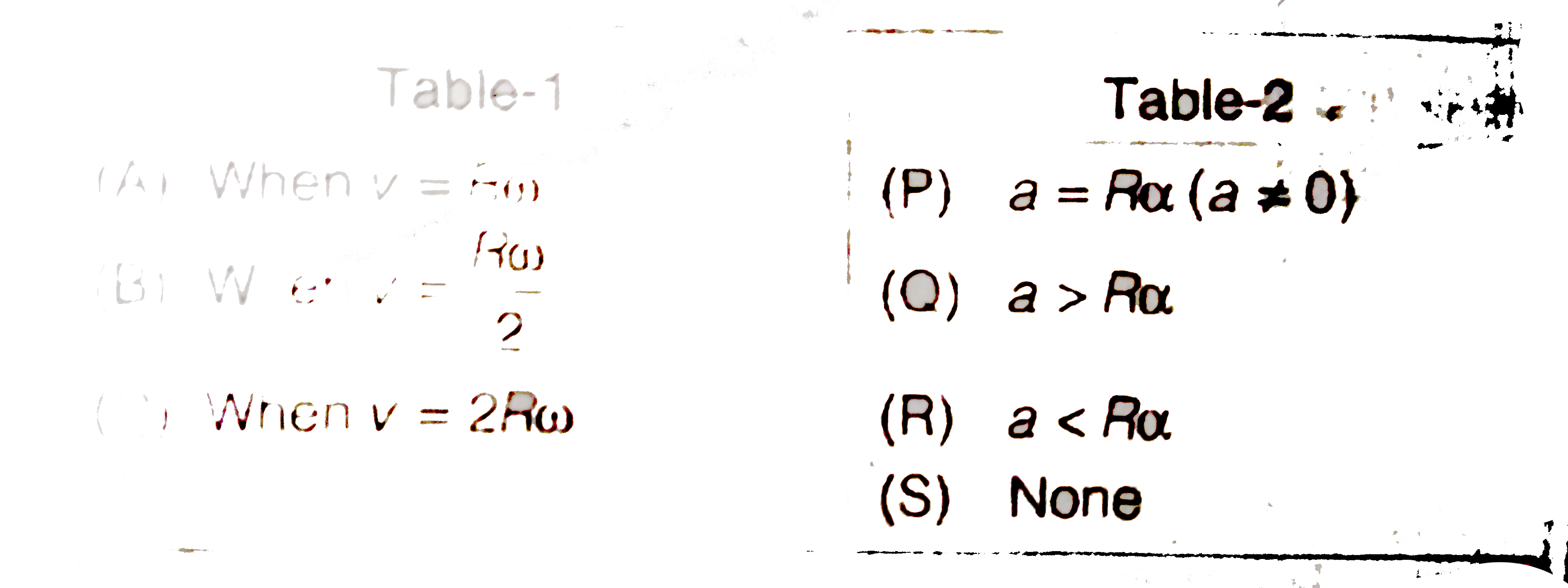

View SolutionA disc with linear velocity v and angular velocity ω is placed on rough ground. Suppose a and α be the magnitudes of linear and angular acceleration due to friction.
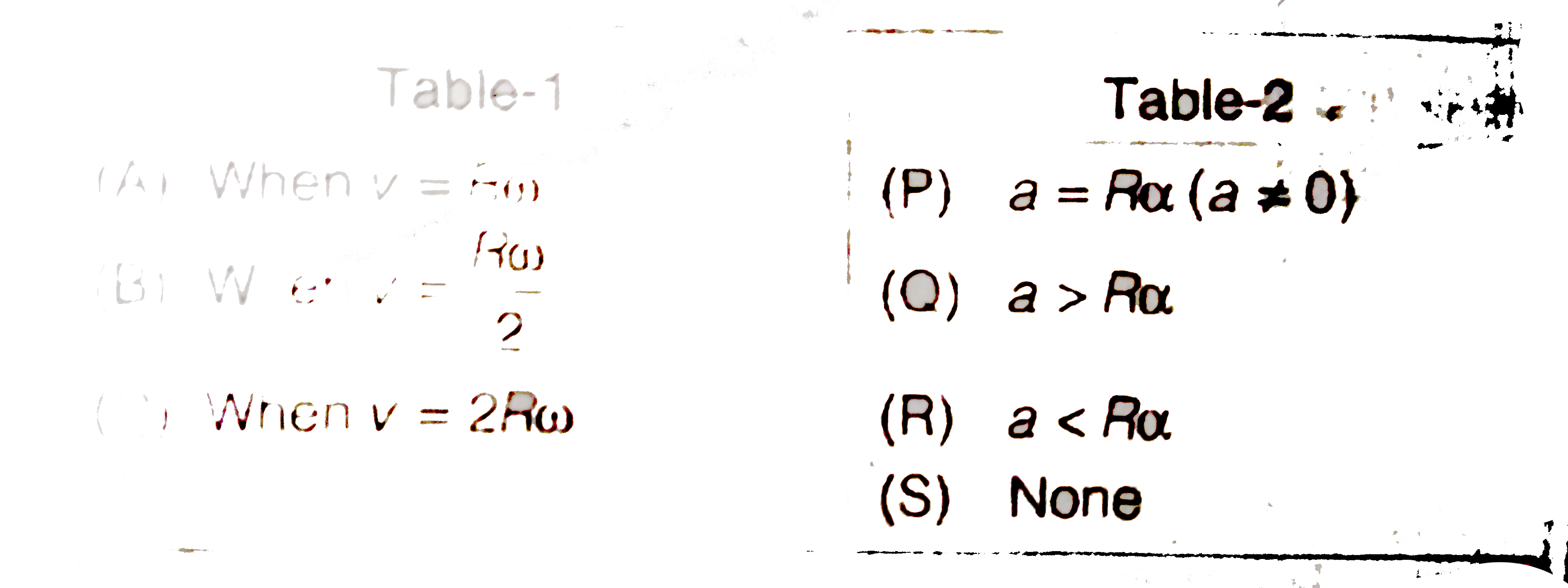

View SolutionA sphere is moving on a smooth surface with angular velocity ω and linear velocity v. If collides elastically with another identical sphere B kept at rest. Neglecting friction everywhere, let VA and ωA be linear and angular velocities of sphere A after the impact and let VB and ωB be the corresponding parameters for spehre B. Then
View Solution
