Question

Derive an expression for magnetic field at the centre of circular current carrying coil.

Explanation

Consider a current carrying coil carrying current I.
O is the centre of the circular coil and a be its radius.
Consider a point P on the axis of this current carrying circular coil at a distance r from the centre of the coil.

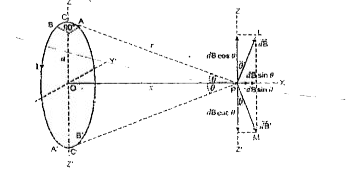
Suppose AB is a small elementary portion of length`dl` at a distance r from the observation point. Every current element is perpendicular to the direction of `vecr`.
According to Biot-Savart.s Law,
Magnetic field at P due to small element AB = dB
and `dB = (mu_0)/(4pi) (I dl sin theta)/(r^2)`
`dB = (mu_0)/(4pi) (I dl)/(r^2) " " [sin theta = sin 90^@ = 1 and theta = 90^@]`
`vec(dB)` is perpendicular to the plane in which `vec(dl)` and `vec(r)` lie and is along PL which is perpendicular to PC.
Resolve dB into two rectangular components
1. `dB cos theta`, which is perpendicular to the axis of the coil.
2. `dB sin theta`, which is along the axis of coil but away from the centre of the coil.
As the coil is symmetrical about its axis, so every element of length `vec(dl)` has an equal and opposite element, for example, AB has an equal and opposite element A.B. at diametrically opposite point D. The magnetic field `vec(dB)` due to the current element A.B. has the magnitude same as that due to the current element AB but its direction is along the PM. Thus,
`|vec(dB)| = |vec(dB)|`
Both `vec(dB)` and `vec(dB.)` can be resolved in two mutually perpendicular components along PX and YY.. The y -components of the magnetic field due to these elements along YY. being equal and opposite cancel each other. Hence, the resultant of these components `(vec(dB) cos)` for the complete loop, from symmetry, is zero. Thus, only the x-component of `vec(dB) = vec(dB) sin phi` survives and this component of magnetic field due to each component of the loop points in the same direction.
Therefore, magnetic field at point P due to whole coil is equal to the sum of `vec(dB) sin phi` components of magnetic field due to each element, i.e.,
`vecB = sum vec(dB) sin phi`
or `vecB = int vec(dB) sin phi " " ...(1)`
Now, `|vec(dB)|` for the current element at P is given by :
`dB = (mu_0I)/(4pi) (dl sin pi/2)/(r^2) " " (as theta = 90^@)`
or `dB = (mu_0 I dl)/(4pir^2)`
Substituting this value of dB is eqn. (1), we have
`B = int (mu_0 I dl)/(4pi r^2) sin phi`
`= (mu_0 I sin phi)/(4pi r^2) xx 2 pi a`
as `I , phi` and r are fixed and
`int dl` = Circumference of the coil `= 2 pi a `
or `B = (mu_0)/(4pi) (2 pi Ia )/(r^2) sin phi" " (2) `
Now from right angld `Delta COP`
`sin phi = a/r = a/(sqrt(a^2 + x^2)) as r = sqrt(a^2 + x^2)`
`therefore B = (mu_0)/(4pi) (2 pi I a)/(r^2) xx a/(sqrt(a^2 + x^2))`
or `B = (mu_0 2 pi I)/(4pi) xx (a^2)/((a^2 + x^2)^(3//2))`
If there are n turns in the coil, then the strength of magnetic field at point P due to the coil will be n times the magnetic field due to a coil of single turn, i.e.,
`B = (mu_0)/(4pi) 2 pi n I xx (a^2)/((a^2 + x^2)^(3//2))" " ....(3) `
If the observation lies at the centre of the coil then `x = 0 `
From eqn. (3),
`B = (mu_0)/(4pi) (2pi n I a^2)/((a^2)^(3//2))`
`B = (mu_0)/(4pi) (2 pi n I)/(a)`
which is required expression for magnetic field at the centre of current carrying circular coil. Magnetic field due to current carrying circular coil can be shown as given aside.