Derive an expression for potential energy of a bar magnet when placed in an external magnetic field.

Video Solution

Text Solution

Verified by Experts

Potential of a bar magnet. The torque $\to τ$ acting on a magnetic dipole placed in a uniform magnetic field $\to B$ is given by :
$\to τ = \to M \times \to B$
or $τ = M B sin θ ... (1)$

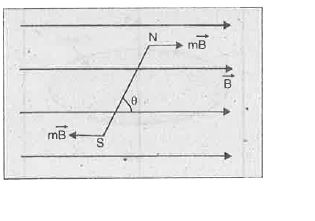
This torque tends to align the magnetic dipole in the direction of $\to B$ . If the dipole is rotated against the action of this torque, work has to be done, which is stored in the form of potential energy of the dipole.
Work done in rotating the dipole through an angle $d θ$ against the torque is given by
$d W = τ d θ = M B sin θ d θ$
If the magnetic dipole is rotated from $θ_{1} and θ_{2}$ , total work done will be
$W = \int d W = M B \int_{θ_{1}}^{θ_{2}} sin θ d θ$
= $- M B ({cos θ}_{2} - {cos θ}_{1})$
This work done is the energy stored U
$∴ U = - M B ({cos θ}_{2} - {cos θ}_{1})$
If the dipole is rotated from
$θ_{1} = 90^{\circ} to θ_{2} = θ$ then
$U = - M B (cos θ - {cos 90}^{\circ})$
$U = - M B cos θ$
or $U = - \to M \cdot \to B$ .

Updated on:21/07/2023

When a bar magnet is placed in a non-uniform magnetic field, it performs
Arotational motion.
Btranslational motion.
Crectilinear motion.
Dboth (A) and (B).
A paramagnetic sample shows a net magnetization of $8 A m^{- 1}$ when placed in an external magnetic field of 0.6 T at a temperature of 4 K When the same sample is placed in an external magnetic field of 0.2 T at a temperature of 16 K, the magnetization will be
A $\frac{32}{3} A m^{- 1}$
B $\frac{2}{3} A m^{- 1}$
C $6 A m^{- 1}$
D $2.4 A m^{- 1}$