Draw the vibration energy of a crystal as a function of frequency (neglecting the zero-point vibrations). Consider two cases: T=Θ/21 and T=Θ/4, where Θ is the Debye temperature.
In the Debye model
dBω=Aω2,0≤ω≤ωm
Then 3N=∫ω00dNω=Aω3m3.(Toltal no.of models is 3N)
Thus A=9Nω3m
we get U=9Nω3m∫ωm0ω2.ħωe−ħω/KT−1dω ignoring zero point energy
=9Nħωm∫10x3dxeħωmx/kT−1,x=ωωm
=9RΘ∫10x3dxexΘ/T−1for0≤x≤1
Thus 19RΘdU(x)dx=x3exΘ/T−1for0≤x≤1
for T=Θ/2, this is x3e2x−1, for
T=Θ4, it is x3e4x−1
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Radioactivity
35 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Nuclear Reaction
42 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Demostrate that molar heat capacity of a crystal at a temperature T<Θ, where Θ is the Debye temperature, is defined by Eq. (6.4f)
View SolutionFigure. 6.10 shows heat capacity of a crystal vs temperatue in terms of the Debye theory. Here Ccl is classical heat capacity Θ is the Debye temperature. Using this plot, find:
(a0 The Debye temperature for silver if at a temperature T=65K its molar heat capacity is equal to 15J(mol.K),
(b) the molar heat capacity of aluminum at T=80K if at T=250K it is equal to 22.4J(mol.K)
(c )the maximum vibration frequency for copper whose heat capacity at T=125K differs form the classical value by 25%.
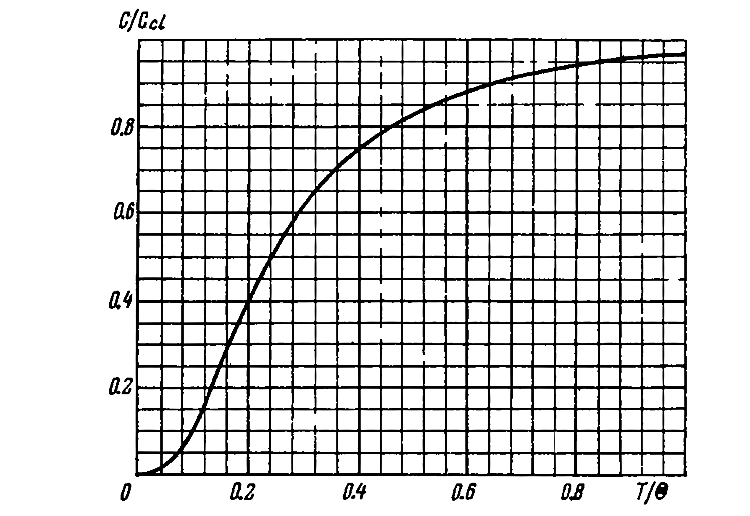
View Solution
Knowledge Check
A gas mixture consists of 2 moles of oxygen and 4 of Argon at temperature T. Neglecting all vibrational modes, the total internal energy of the system is
A4 RTB9 RTC11 RTD15 RTA gas mixture consists of 2 moles of oxygen and 4 of Argon at temperature T. Neglecting all vibrational modes, the total internal energy of the system is
A4 RTB15 RTC9 RTD11 RT
Calculate the mean zero-point energy per one oscillator of a crystal in terms of Debye theory if the Debye temperaute of the crystel is equal to Θ.
View SolutionCalculate the zero-point energy per one gram of copper whose Debye temperature is Θ=330K.
View SolutionDerive the formula expressing molar heat capacity of a unidimensional crystal, a chain of identical atoms, as a function of temperature T if the Debye temperature of the chain is equal ot Θ. Simplyfie the octained expression for the case T>Θ
View SolutionEvaluate the proprgation velcocity of acoustic vibrations in aluminum whose Debye temperature id Θ=396K.
View SolutionA gaseous mixture consists of 16 g of O2 and 16 g of He at temperature T. Neglecting the vibrational modes, total internal energy of the system is
View SolutionA gas mixture consists of 2 moles of oxygen and 4 of Argon at temperature T. Neglecting all vibrational modes, the total internal energy of the system is
View Solution
