Few rods of material X and Y are connected as shown in figure - 4.10. The cross sectional area of all the rods are same. If the end A is maintained at 80∘C and the end F is maintained at 10^(@)C~ . Calculate the temperatures of junctions B and E in steady state . Given that thermal conductivty of material X is double that of Y.
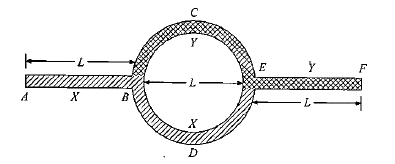
We first find the thermal resistances of the different rods shown in figure - 4.10 these are given as
RAB=1kx.LA
RBCE=1ky.π1/2A
RBDE=1kX.π1/2A
REF=1ky.LA
Now in steady state the amount of heat flow end E to F remains constant as there is no absorption of heat . Then we must have that the amount of heat coming at junction B is equal to the amount of heat having B and same statement can be given for junction E. If temperature of junction B and E are taken as TB and TE then we have for junction B.
TA−TBRAB=TB−TERBCE+TB−TERBDE
or 80−TB1/kX.L/A=TB−TE1/kY.πL/2A+TB−TE1/kX.πL/2A
or 80−TB=(TB−TEπ)+(TB−TE2π) [AskX=2kY]
or 80−TB=32π(TB−TE)..(4.14)
Similarly for junction E, we can write
TB−TERBCE+TB−TERBDE=TE−10REF
or TB−TE1/kY.πL/2A+TB−TE1/kX.πL/2A+TE−101/kY.L/A
or 2(TB−TE)π+4(TB−TE)π=TE−10
or 34π(TB−TE)=TE−10
Solving equation -(4.14) and (4.15), we get
TE=19.74∘C
and TB=60.52∘C
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.6
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.7
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.4
1 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
Two rods of material, x and two of y are connected as shown in the figure. All the rods are indentical in length and cross-sectional area. If the end A is maintained at 80∘C and the end D is maintained at 10∘C, calculate the temperature of the junctions B and C in the steady state. Thermal conductivity of x is double that of y.

View SolutionA few rods of materials X and Y are connected as shown in The cross-sectional areas of all the rods are same if the end A is maintaind at 80∘C and the end F is maintained at 102C If the temperature of junctions B and E in steady state are 39.48∘Cn1 and 60.52∘Cn2 Find n1 and n2 Given thermal conductivity of material X double that of Y
 .
.
View Solution
Knowledge Check
Seven identical rods of material of thermal conductivity K are connected as shown in figure. All the rods are of identical length L and cross sectional area A1. If one end A is kept at 100∘C and the other end B is kept at 0∘C, what would be the temperature of the junctions C, D and E (TC,TD and TE) in the steady state?
 ATC>TE>TDBTC=TD=37.5∘C,TE=50∘CCTC=62.5∘C,TD=37.5∘C,TE=50∘CDTC=60∘C,TD=40∘C,TE=50∘C
ATC>TE>TDBTC=TD=37.5∘C,TE=50∘CCTC=62.5∘C,TD=37.5∘C,TE=50∘CDTC=60∘C,TD=40∘C,TE=50∘CThe end A of rod AB of length 1 m is maintained at 80∘C and the end B at 0∘C. The temperature at a distance of 60 cm from the end A is
A16∘CB32∘CC48∘CD64∘CSeven identical rods of matrical of thermal conductivity k are connected as shown in All the rod are of identical length l and cross sectional area A if the one end b is kept at 100∘C and the other end is kept at 0∘C The temperatures of the junctions C,D and E(θDandθE) be in the steady state
 .AθC>θE>θDBθE=50∘CandθD=37.5∘CCθE=50∘C,θC=62.5∘CandθD=37.5∘CDθE=50∘C,θC=60∘CandθD=40∘C
.AθC>θE>θDBθE=50∘CandθD=37.5∘CCθE=50∘C,θC=62.5∘CandθD=37.5∘CDθE=50∘C,θC=60∘CandθD=40∘C
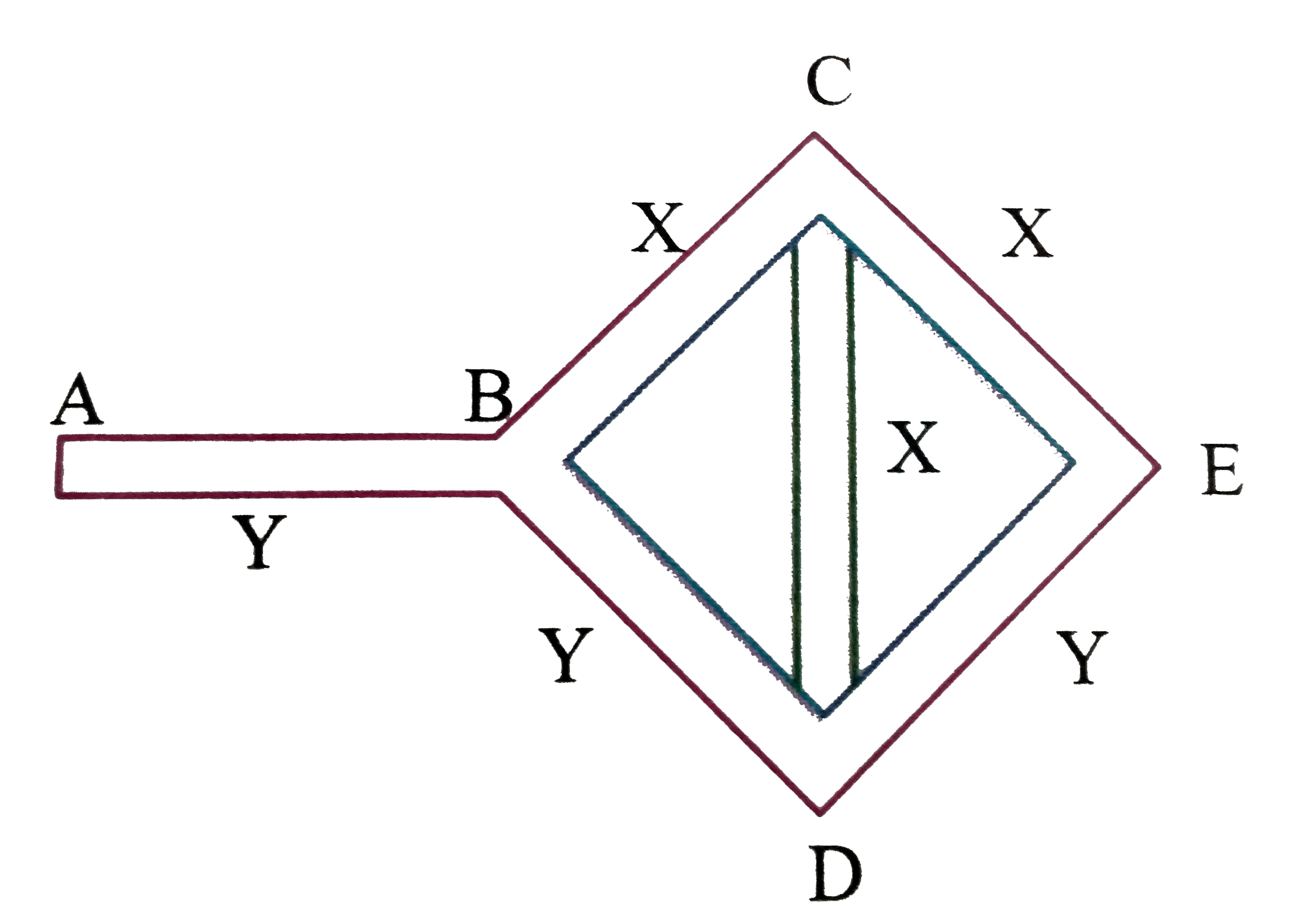
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.

View SolutionThree rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.

View SolutionThree rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1^(@)C^(-1)andtˆofyis400Wm^(-1)^(∘)C−1 .

View Solution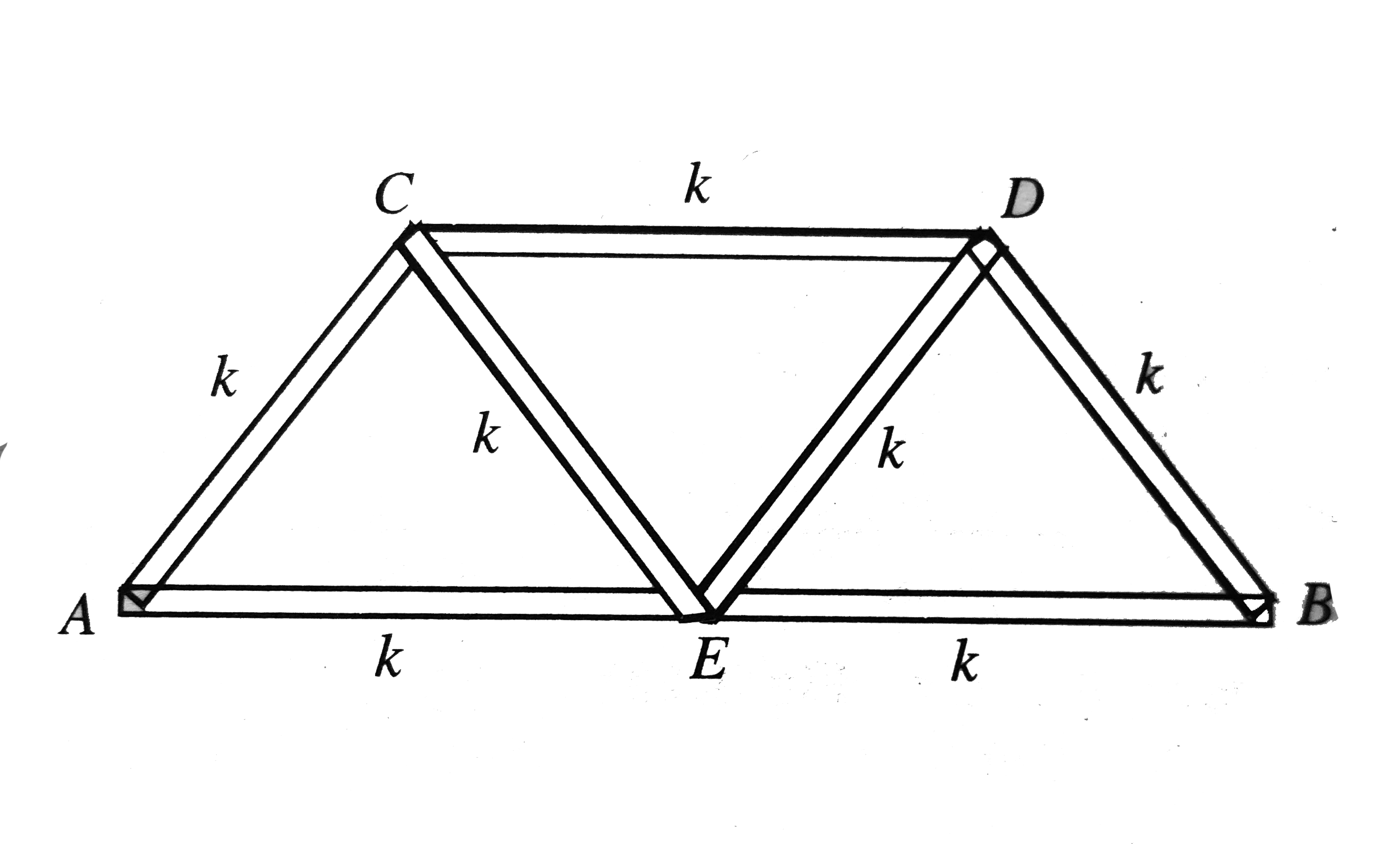
Seven identical rods of material of thermal conductivity k are connected as shown in Fig. All the rods are of identical length l and cross sectional area A If the one end B is kept at 100∘C and the other end is kept at 0∘C what would be the temperatures of the junctions C, D and E(θC,θ)D and θE) in the steady state?
View SolutionThree rods of material 'x' and three rods of materialy are connected as shown in All the rods are of identical length and cross section If the end A is maintained at 60∘C and the junction E at 10∘0C find effective Thermal Resistance Given length of each rod =1 area of cross-section =A conductivity of x=K and conductivity of y=2K
 .
.
View Solution
