Figure 11-16a shows a safe (mass M = 430 kg) hanging by a rope (negligible mass) from a boom (a = 1.9 m and b = 2.5 m) that consists of a uniform hinged beam (m=85 kg) and horizontal cable (negligible mass).
Find the magnitude F of the net force on the beam from the hinge.
Now we want the horizontal component and vertical component F, so that we can combine them to get the magnitude of the net force.Because we know , we apply the force balancing equations to the beam.
Calculations: For the horizontal balance, we can rewrite
and so
For the vertical balance, we write as
Substituting Mg for and solving for , we find that
= 5047N
From the Pythagorean theorem, we now have
Note that F is substantially greater than either the combined weights of the safe and the beam, 5000 N, or the tension in the horizontal wire, 6100 N.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - EXAMPLE1videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT4videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
Figure 11-16a shows a safe (mass M = 430 kg) hanging by a rope (negligible mass) from a boom (a = 1.9 m and b = 2.5 m) that consists of a uniform hinged beam (m=85 kg) and horizontal cable (negligible mass).
What is the tension Tc in the cable? In other words, what is the magnitude of the force →Tc on the beam from the cable?View SolutionA weight of mass m is suspended from a hinged bracket (Fig.).
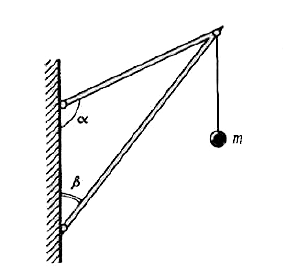
Find the forces in the rods making up the bracket.View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
A32mgB2mgC52mgD3mg - Question 2 - Select One
Two points masses of 2 kg and 3 kg lie at 5 m and 9 m away from origin O respectively. Find out the distance of centre of mass of these point masses from the origin.
A14.2 mB7.4 mC20 mD6 m - Question 3 - Select One
In the figure, blocks A and B of masses 2m and m are connected with a string and system is hanged vertically wioth the help of spring. Spring has negligible mass. Find out magnitude of acceleration of masses 2 m and m just after the instant when the string is cut
Ag,gBg,g2Cg2,gDg2,g2
A force F is applied horizontally on mass m1 as shown in figure. Find the contact force between m1 and m2
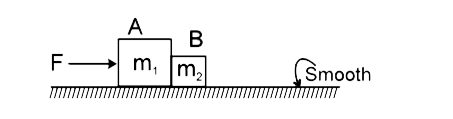 View Solution
View SolutionFigure 5-59 shows a box of mass m2=1.0 kg on a friction-less plane inclined at angle θ=30∘. It is connected by a cord of negligible mass to a mass m1=2.5 kg on a horizontal frictionless surface. The pulley is frictionless and massless. (a) If the magnitude of horizontal force →F is 2.3 N, what is the tension in the connecting cord? (b) What is the largest value the magnitude of →F may have without the cord becoming slack?
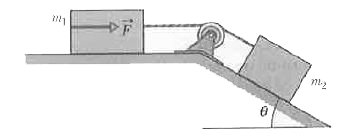 View Solution
View SolutionA uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is μs determine an expression for the maximum mass M that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at P in terms of m,M and μs
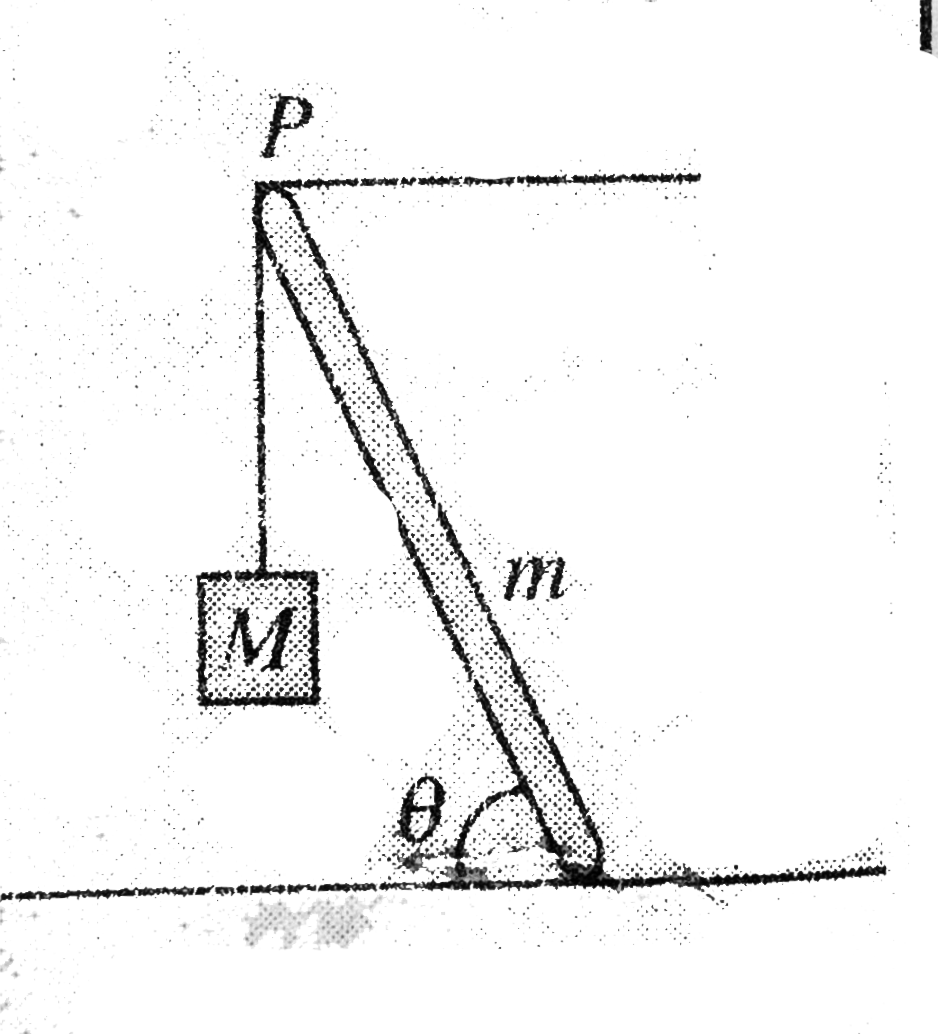 . View Solution
. View SolutionTwo particles of mass 5 kg and 10 kg respectively are attached to the two ends of a rigid rod of length 1 m with negligible mass. the centre of mass of the system from the 5 kg particle is nearly at a distance of :
View SolutionA block of mass 2 m is pulled along a horizontal frictionless surface by a rope of mass m as shown in the figure given. What force is exerted by the rope on the block ?
 View Solution
View Solution

