Figure shown two blocks in contact sliding down an inclined surfase of inclination $30^{\circ}$ . The friction coefficient between the block of mass $4.0 k g$ and the incline is $μ_{2} = 0.30$ . Find the acceleration of $2.0 k g$ block. $(g = 10 m / s^{2})$

Video Solution

Text Solution

Verified by Experts

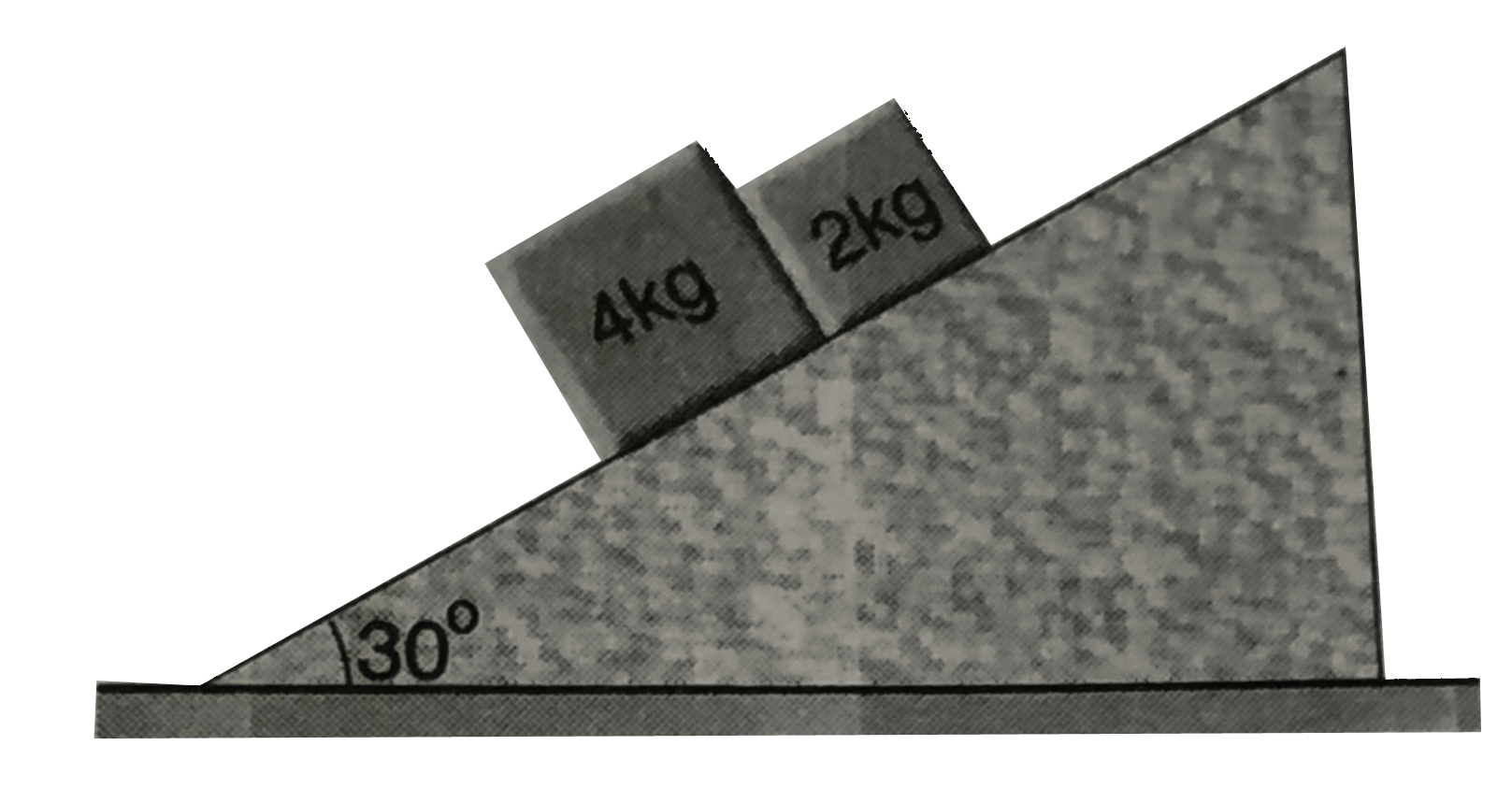
Since $μ_{1} < μ_{2}$ ,acceleration of $4 k g$ block, if allowed to move seperately. But as the $2.0 k g$ block is behind the $4.0 k g$ block both of them will move with same acceleration say $a$ . Taking both the block as a single system,
Force down the plane on the system $= (4 + 2) g {sin 30}^{\circ}$
$= (6) (10) (\frac{1}{2}) = 30 N$
Force up the plane on the system
$= μ_{1} (2) (g) {cos 30}^{\circ} + μ_{2} (4) (g) {cos 30}^{\circ}$
$= (2 μ_{1} + 4 μ_{2}) g {cos 30}^{\circ}$
$= (2 \times 0.2 + 4 \times 0.3) (10) (0.86)$
$= 13.76 N$
:. Net force down the plane is $F = 30 - 13.76 = 16.24 N$
:. Acceleration of both the block down the plane will be $a$ .
$a = \frac{F}{4 + 2} \frac{16.24}{6} = 2.7 m / s^{2}$

Updated on:21/07/2023