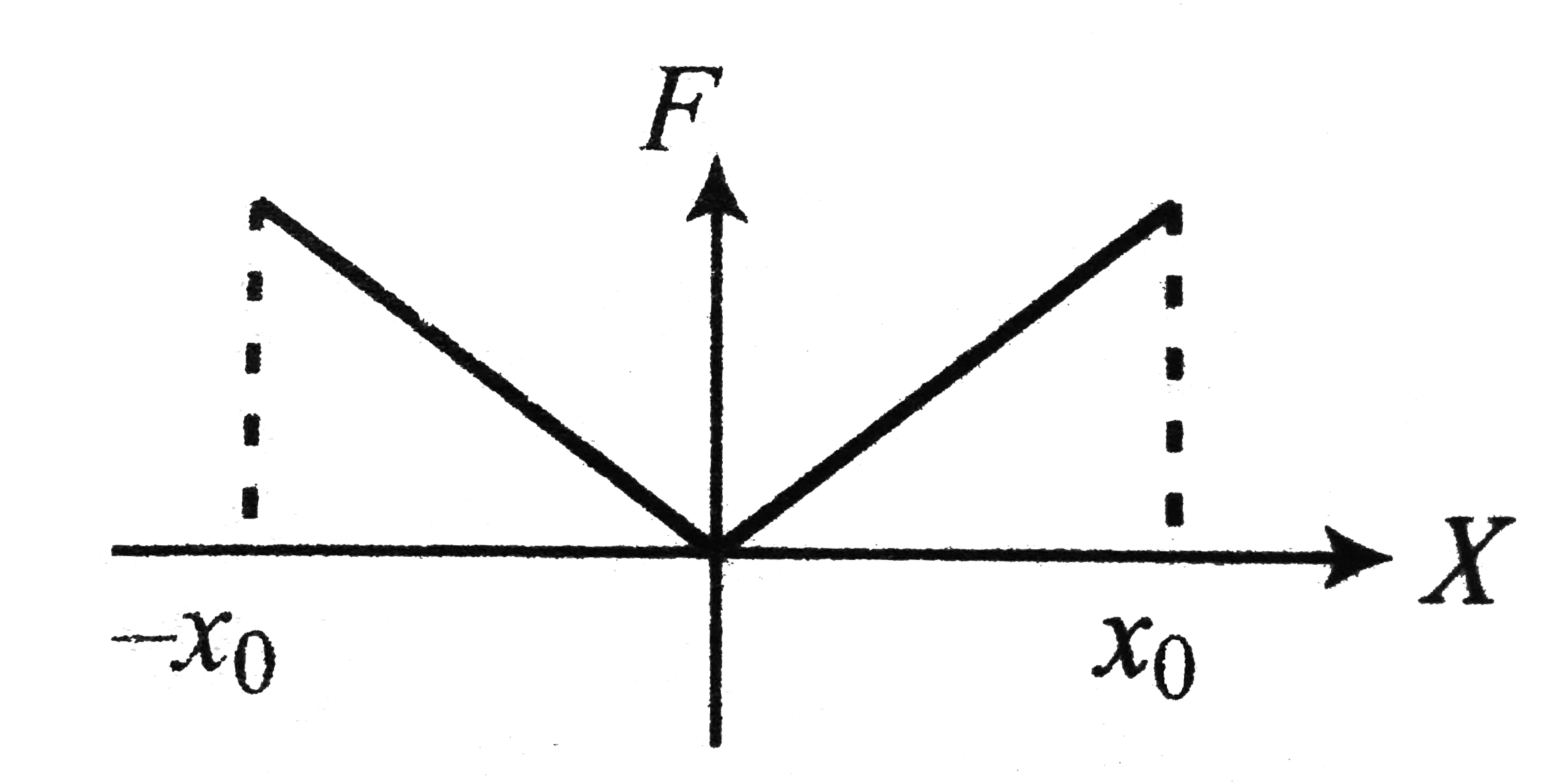
Figure shows a plot of the conservative force F in a unidimensional field. The plot representing the function corresponding to the potential energy (U) in the field is
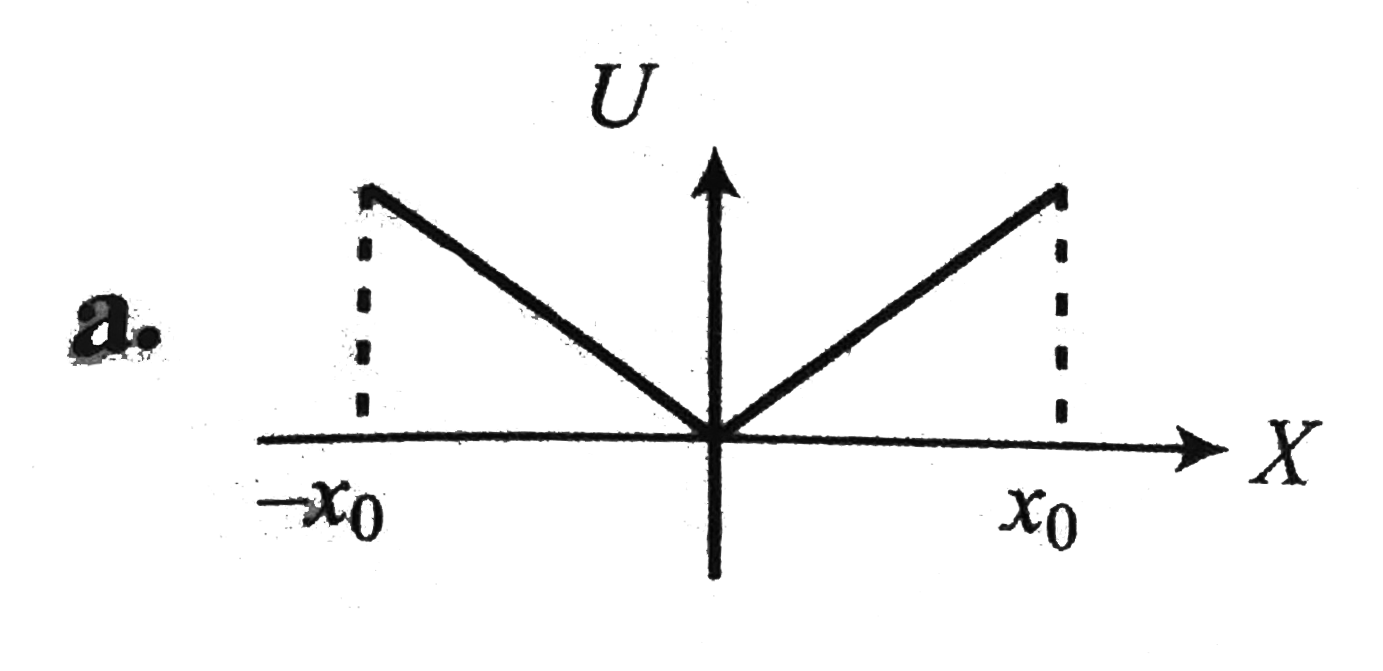

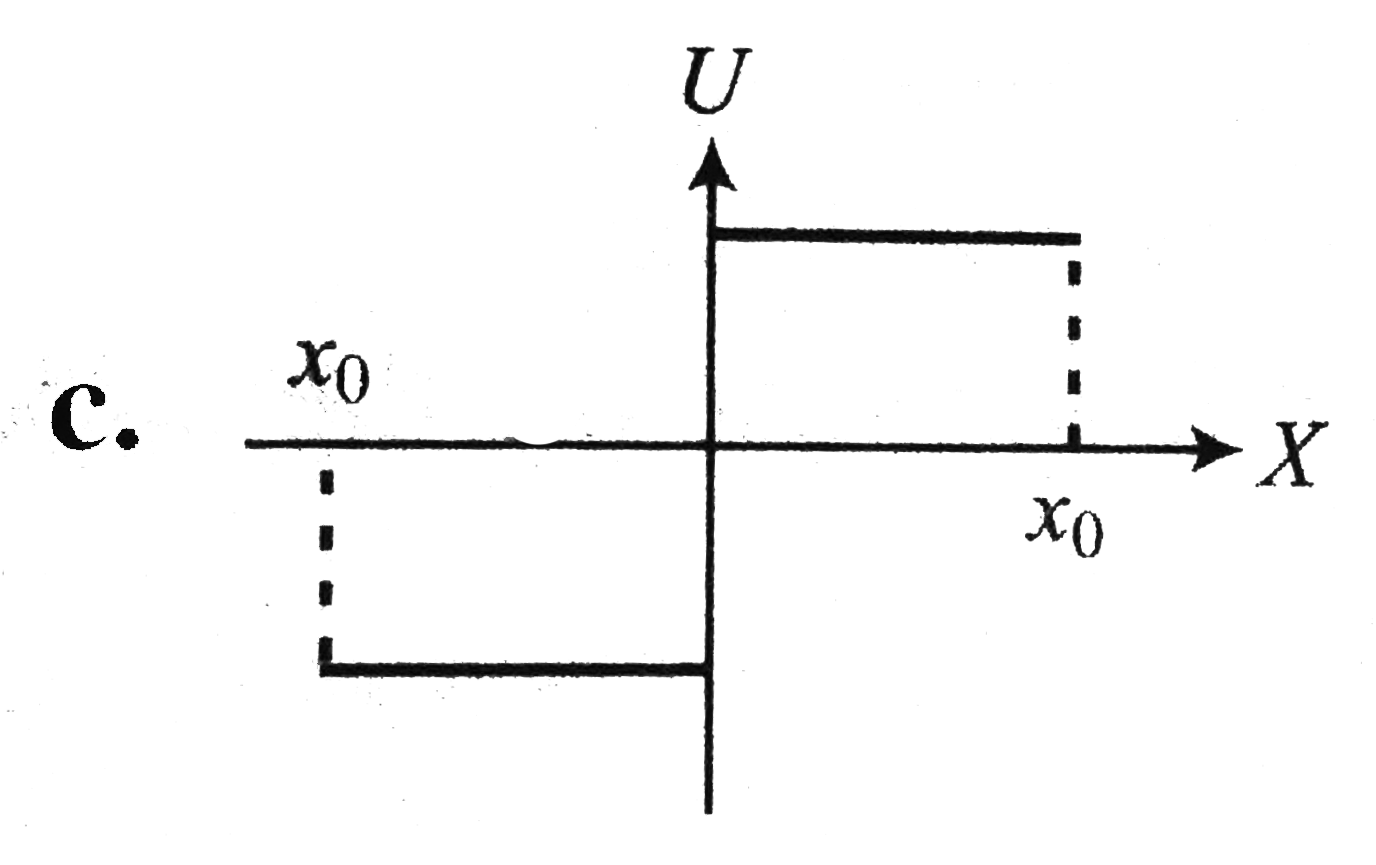
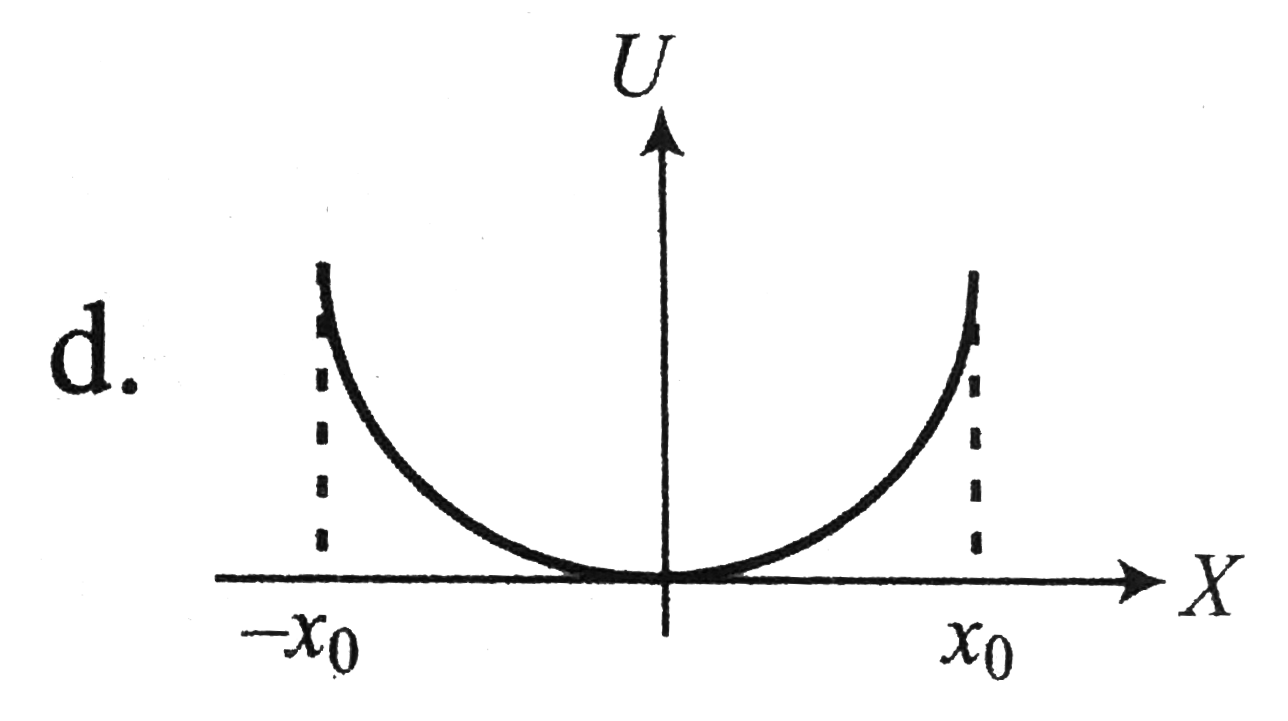
The correct Answer is:D
f(x)=−dUdx(x) or U(x)=−∫F(x)dx
Here F(x)=−kx, where k is a positive constant.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Knowledge Check
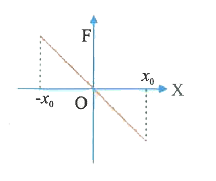
Figure given below shows the plot of the conservative force F, in a unidimensional field. The plot representing the function corresponding to the potential energy (U) in the field is :
 A
A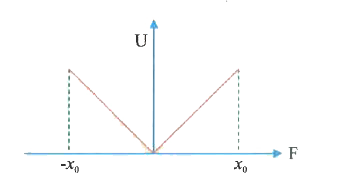 B
B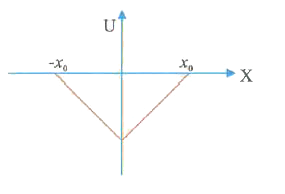 C
C D
D
The relation between conservative force and potential energy U is given by :–
A→F=dUdxB→F=∫UdxC→F=−dUdxD→F=d2Udx2An electric dipole in a uniform electric field has potential energy U. The magnitude of the torque acting on the dipole due to the field is τ.
AU is minimum and τ is zero when the dipole is perpendicular to the field.BU is zero and τ is a maximum when the dipole is perpendicular to the field.CU is a minimum and τ is a maximum when the dipole is perpendicular to the field.DU is a minimum and τ is zero when the dipole is anti-parallel to the field.
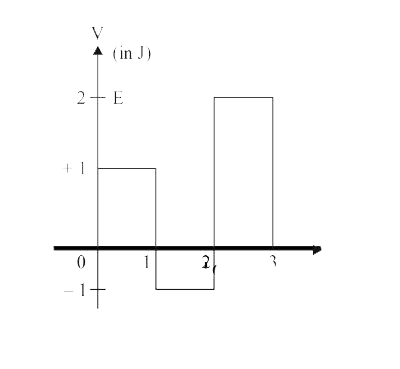
The potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.
View SolutionFind the expresstion of potential energy U(x,y,z) for a conservative force in a force field where force is given as →F=yzˆi+xyˆk Consider the zero of the potential energy chosen at the point (2,2,2).
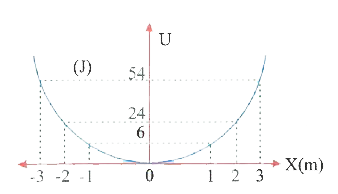
View SolutionFigure given below shows the variation of potential energy function U(x), corresponding to a particle lying in a one dimensional force field. The force acting on the particle at x = 2 m is:
View SolutionFigure given below shows the variation of potential energy function U(x), corresponding to one dimensional force field. The point on the graph representing the position of most stable equilibrium is :
(##NAR_NEET_PHY_XI_P2_C06_E09_112_Q01.png" width="80%">
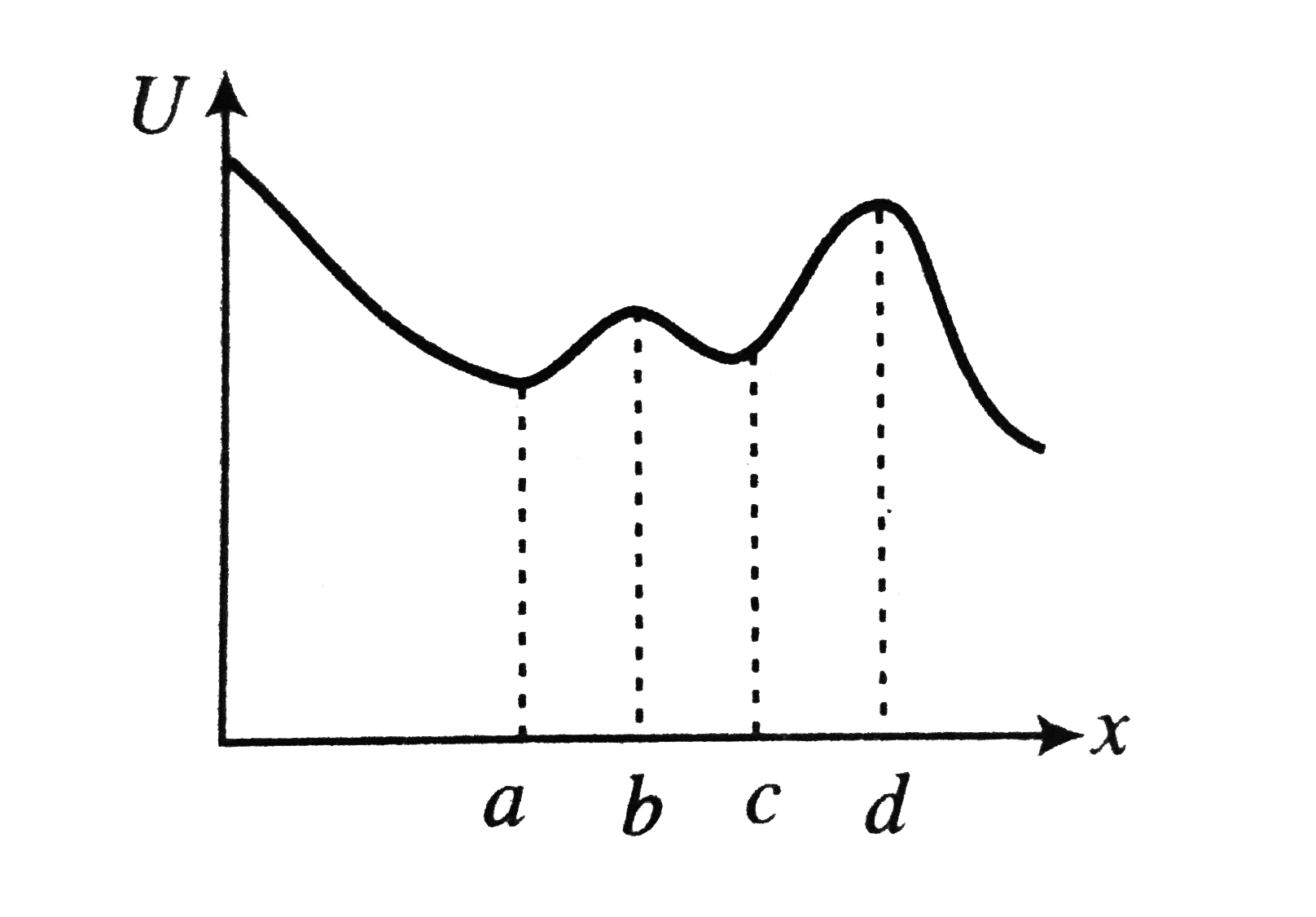
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
View Solution