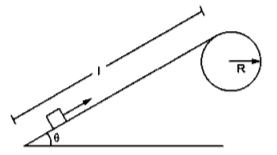
Figure shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. a.Find the minimum projected speed v0 for which the particle reaches the top of the track. b. Assuming that the projection speed is 2v0 and that the block does not lose contact with the track before reading its top, find teh force acting on it whenit reaches the top. c. Assuming that teh projection speed is only slightly greater than v0 where will the block lose contact with the track?
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B, C, D
a. Net force on the particle A and B, F=mgsinθ
work done to reach B,
W=FS=mgsinθl
Again work done to reach B to C
=mgh
=mghR(1−cosθ)
So,→talworkdo≠<br>=mg(lsintheta+r(1-costheta)]<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C08_E01_099_S01.pngwh=80%mx-autosty≤=background:white;><br>Now,chan≥∈K.E.<br>=workdo≠<br>rarr 1/2mv_2^2=mg[lsintheta+R(1-costheta)]<br>rarr v_2=sqrt(2g[R(1-costheta)+lsintheta]<br>b.Whentehblockisprojectedataspeed2v_0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C08_E01_100_S01.pngwh=80%mx-autosty≤=background:white;><br>LetthevelocityofCwillbev_0.<br>Apply∈ge≠rgyypricip≤<br>(1/2)mv_0^2 -(1/2)m(2v_0)^2<br>=−mg[lsinθ+R(1−cosθ)]
rarr V^2=4v_0^2-2g[lsintheta+R(1-costheta)]<br>=4.2g[lsintheta+R(1-costheta)]- 2g[lsintheta+R(1-costeta)]<br>soforceact∈gontehbody<br>rarr N=V^2/R=6mg[(l/R)sintheta+1-costheta]<br>c.Letthel∞secontactaftermak∈gan∠theta<br>(mv^2)/R=mgcostheta<br>rarr v^2=Rgcostheta.......i<br>Again 12mv2=mg(R−Rcosθ)
→v2=2gR(1−cosθ).........ii
Formiandiicostheta =2/3
→θ=cos−1(23)
Topper's Solved these Questions
Similar Questions
A heavy stone is thrown from a cliff of height h with a speed v. The stone will hit the ground with maximum speed if it is thrown
View SolutionA wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0 at t=0. Where will this maximum be located at t=5s?
View SolutionOn an inclined plane two particles A and B are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of A and B is cot theta , where theta is the angle at which B is projected measured from inclined plane, find the angle at which particles are projected.
View SolutionA small ball is rolled with speed u from point A along a smooth circular track as shown in figure. If x=3R , then What is the minimum value of x for which the ball can reach the point of projection after reaching C?
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionIn the figure shown, a particle is released from the position A on a smooth track. When the particle reaches at B, then normal reaction on it by the track. When the particle reaches at B, then normal reaction on it by the track is
View SolutionA small block is projected into each of the four tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in
View SolutionA particle is projected horizontally with a speed ''u'' rom the top of plane incline at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed ''u'' rom the top of plane incline at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed ''u'' rom the top of plane incline at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontally with a speed "u" from the top of plane incline at an angle ..θ.. with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed "u" from the top of plane incline at an angle ..θ.. with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will particle strike the plane?
View SolutionA particle is projected horizontally with a speed "u" from the top of plane incline at an angle "θ" with the horizontal. How far from the point of projection will the particle strike the plane?
View Solution
