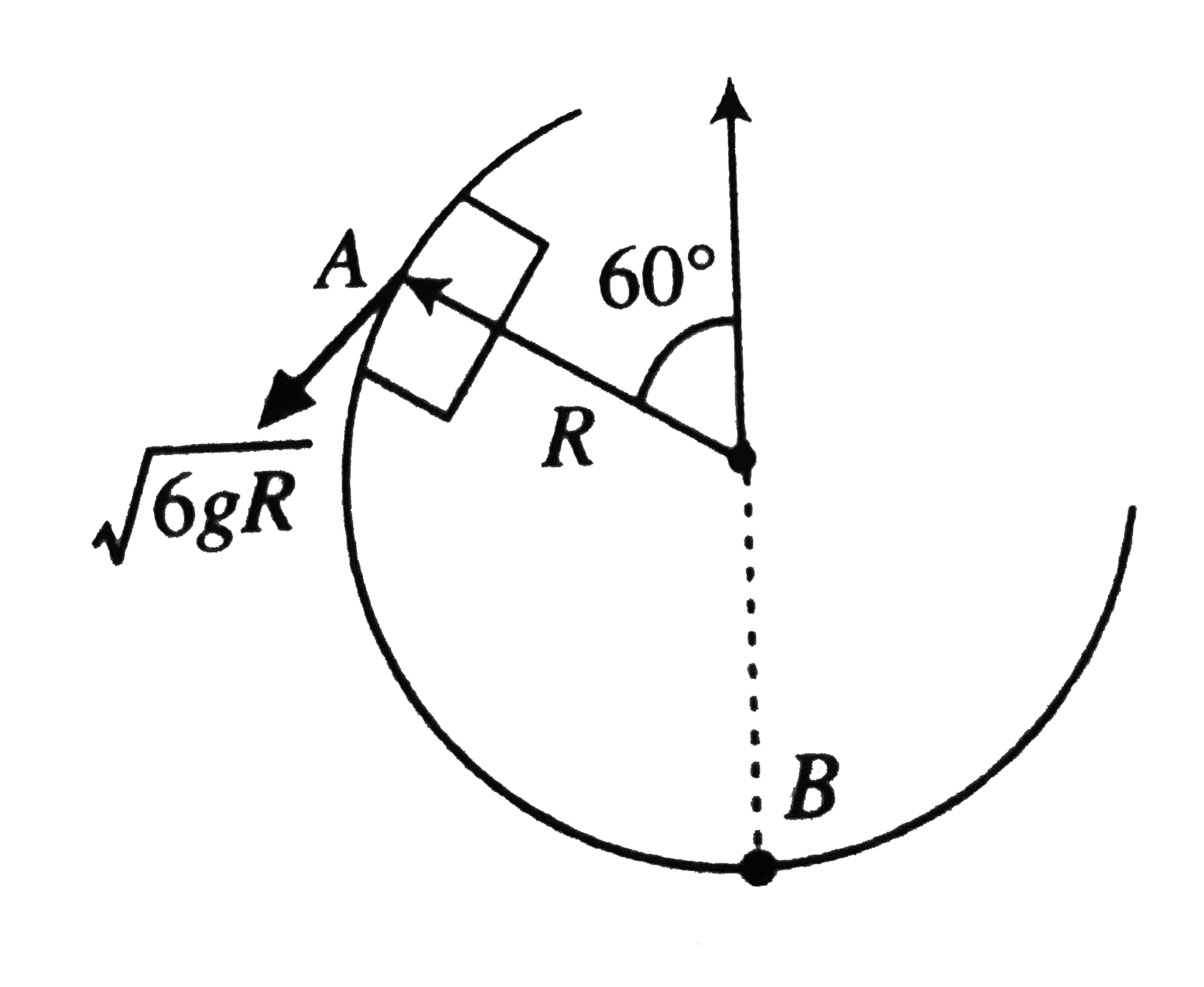
Figure shows a smooth vertical circular track AB of radius R. A block slides along the surface AB when it is given a velocity equal to √6gR at point A. The ratio of the force exerted by the track on the block at point A to that at point B is
0.25
0.35
0.45
0.55
The correct Answer is:D
NA+mgcos60∘=mv2AR
NA=mv2AR−mgcos60∘
=6mg−0.5mg=5.5mg
12mv2A+mgR(1+cos60∘)=12mv2B
v2A+2gR(1+12)=v2B
6gR+3gR=v2B
v2B=9gR⇒vB=√9gR
NB=mg+mv2BR=10mg

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective23videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
AOB is a smooth semicircular track of radius r. A block of mass m is given a velocity √2rg parallel to track at point A. Calculate normal reaction between block and track when block reaches at point O.
 View Solution
View SolutionA particle tied to a string describes a vertical circular motion of radius r continually. If it has a velocity √3gr at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is
View Solution
Knowledge Check
- Question 1 - Select One
A particle tied to a string describes a vertical circular motion of radius r continually if it has a velocity √3gr at the highest point, then the ratio of the respective tensions in the string holding it at the highest point and lowest points is:
A4:3B5:4C1:4D3:2 - Question 2 - Select One
A block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
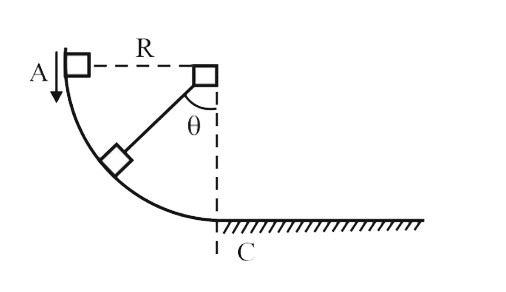 Aμ=sinθcotθ+v2RgBμ=sinθcosθ+v2RgCμ=tanθcosθ+v2RgDμ=cosθtanθ+v2Rg
Aμ=sinθcotθ+v2RgBμ=sinθcosθ+v2RgCμ=tanθcosθ+v2RgDμ=cosθtanθ+v2Rg - Question 3 - Select One
A small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R/2 and spring constant K. The other end of spring is connected to a point at height R/2 directly above the centre of track.

Consider block to be at rest at top most point A of track. If the block is slowly pushed from rest at the highest A. When the spring reaches in horizontal state, then.ASpring potential energy is (3kR24)(2−√3)BSpring potential energy is (kR28)(√3−1)2CGravitational potential energy (taking U=0atθ=0) is (mgR2)DGravitational potential energy (taking U=0atθ=0)is(3mgR8)
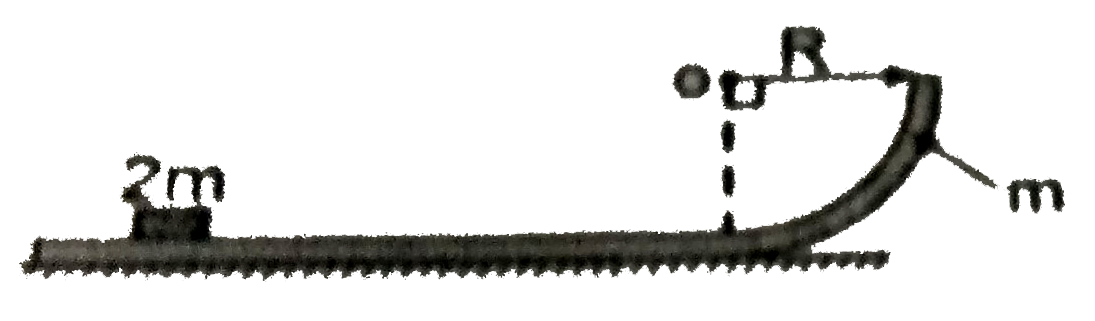
Mass 2m is kept on a smooth circular track of mass m which is kept on a smooth horizontal surface. The circular track is given a horizontal velocity √2gR towards left. Find the maximum height reached by 2m.
 View Solution
View SolutionFigure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.
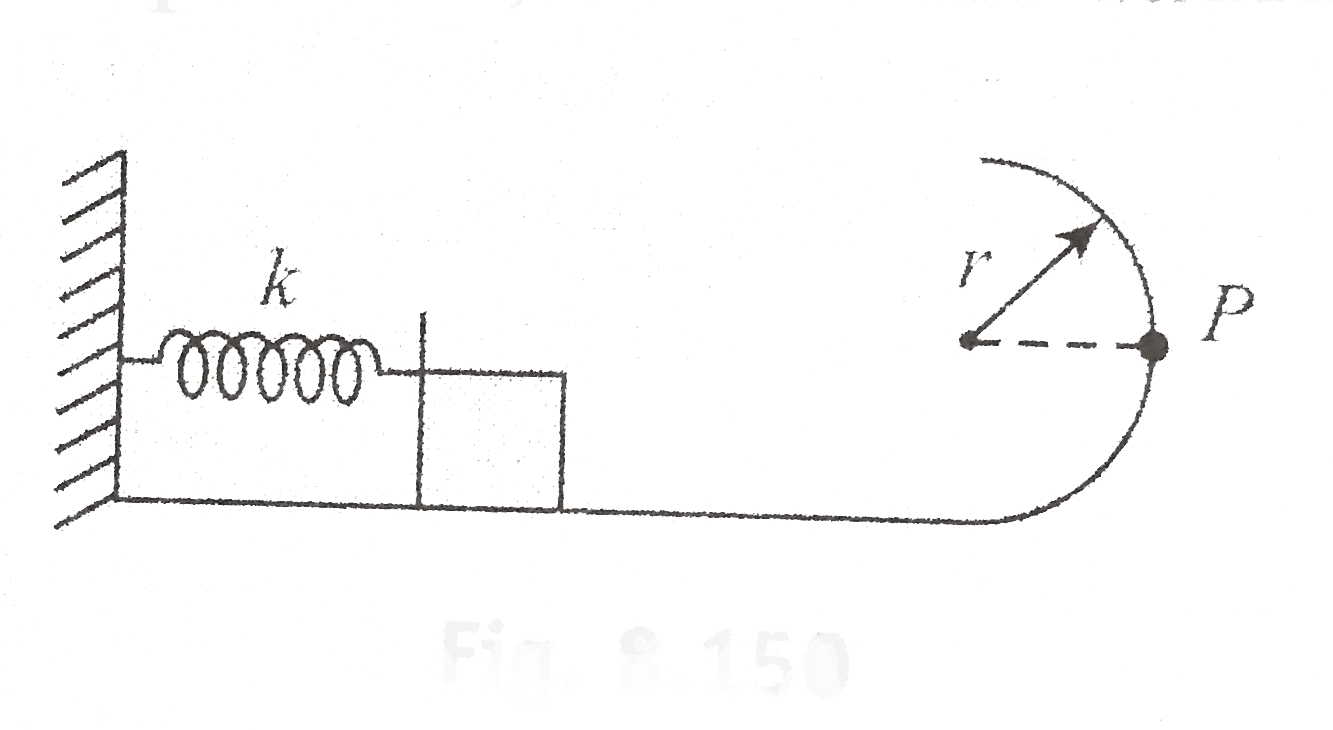 View Solution
View SolutionIn a fixed quarter circular track of radius R which lies in a vertical plane, a block is released from point A and it leaves the path at point B. The radius of curvature of its trajectory when it just leaves the path will be
 View Solution
View SolutionA block of mass m is projected on a smooth horizontal circular track with velocity v what is the average normal force exered by the circular walls on the block during motion A to B?
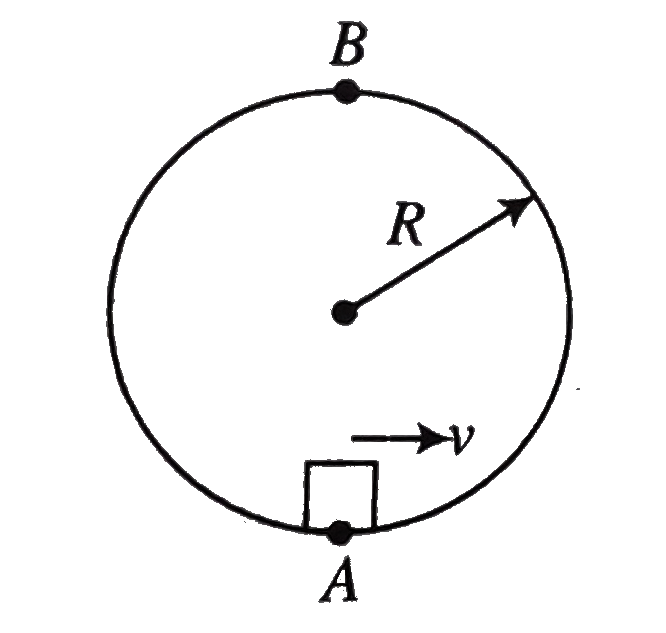 View Solution
View SolutionA block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R.
What is the magnitude of the normal force exerted on the block by the hoop when the block has reached the bottom ?View Solution

