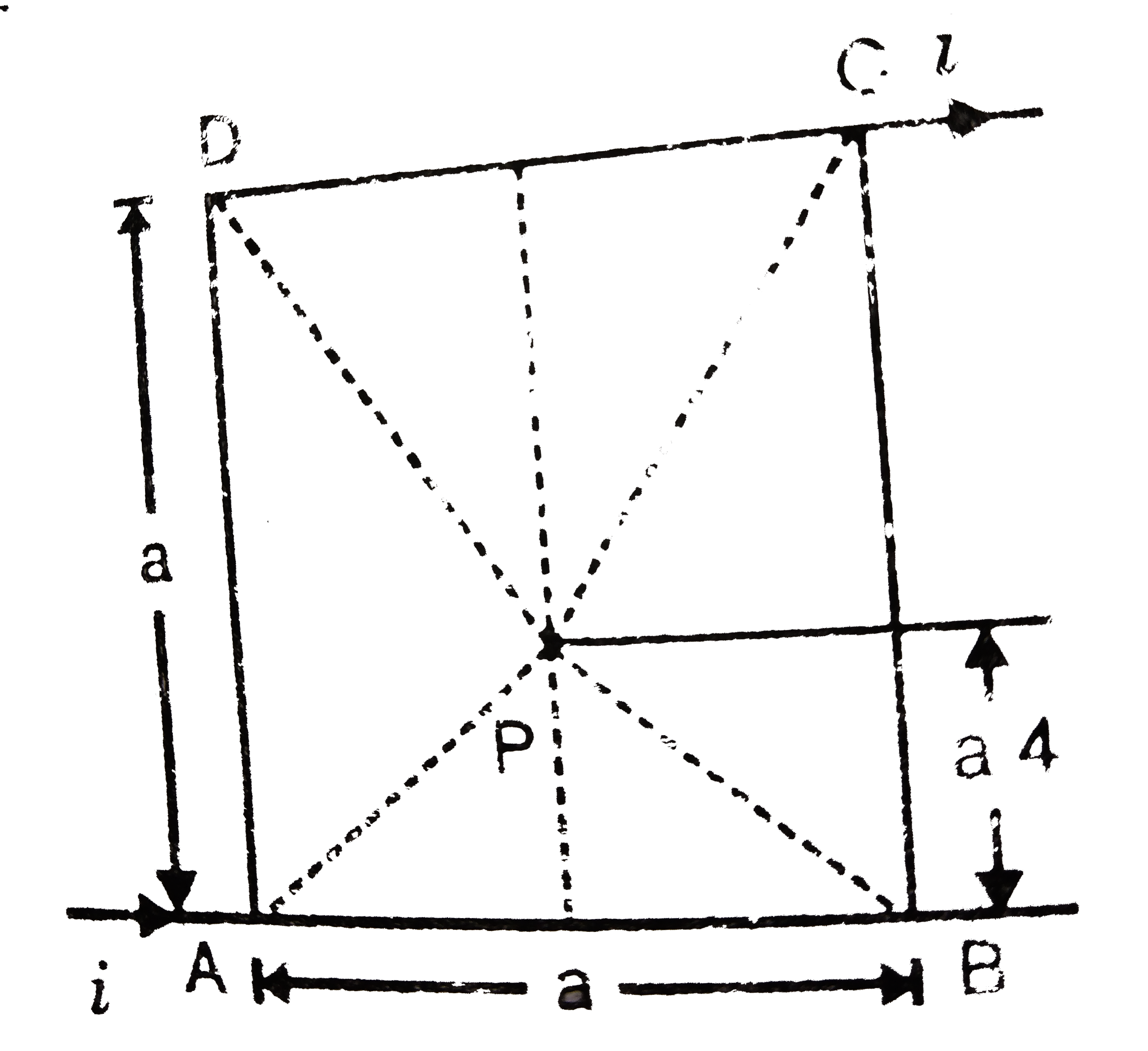
Figure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
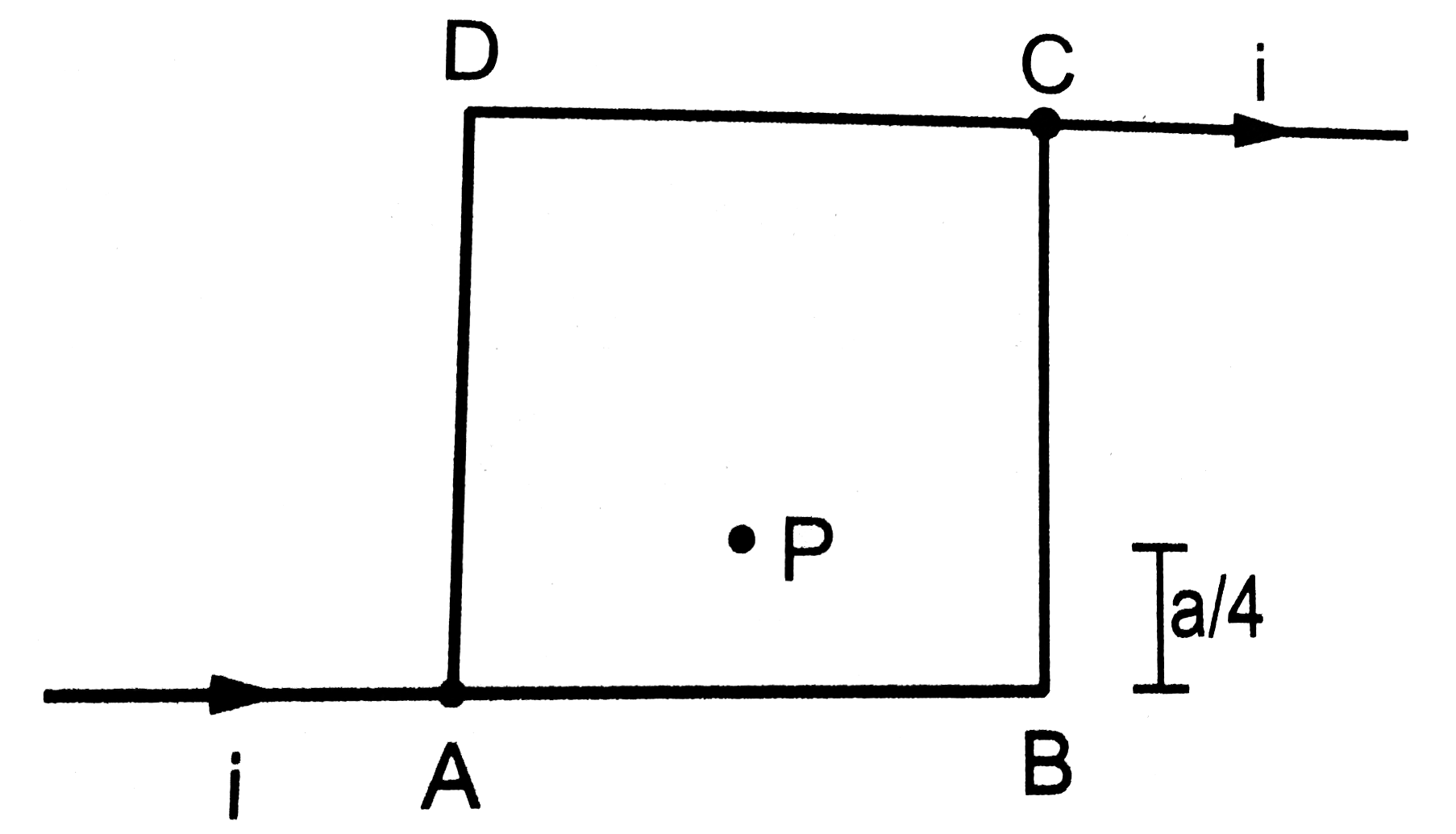
B at P due to AD =μo4π.i2.4a2.a⎡⎢
⎢
⎢
⎢⎣(a2)√(a2)2+(a4)2+(a2)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦along
=μoi2πa⎡⎢
⎢
⎢
⎢⎣(a2)√(a2)2+(a4)2+(a2)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦ along<br>BatPdue→AC=(mu_o)/(4pi).(i)/(2). (16)/(9a^2.a 2.[(((3a)/(4)))/(sqrt(((3a)/(4))^2 + ((a)/(2))^2))<br>(4mu_oi)/(9pia) [(((3a)/(4)))/(sqrt(((a)/(4))^2 +((3a)/(2))^2))]along<br>B at P due to AB = (mu_oi)/(4pi).(i)/(2) . (16)/(9a^2). a. 2 [(((a)/(4)))/sqrt(((a)/(4))^2 + ((a)/(2))^2 along<br>BatPdue→BC = (mu_o)/(4pi).(i)/(2). (4)/(a^2).a. [(((a)/(2)))/ sqrt(((a)/(2))^2 + ((a)/(2))^2) +(((a)/(2)))/sqrt(((a)/(2))^2 + ((3a)/(4))^2)] along<br>=(um_oi)/(2pia)[(((a)/(2)))/sqrt(((a)/(2))^2 +((a)/(2))^2) + (((a)/(2)))/(sqrt(((a)/(2))^2 +((3a)/(4))^2))]along⊗<br>so,net B=4μoiπa⎡⎢
⎢
⎢
⎢⎣(a4)√(a2)2+(a4)2⎤⎥
⎥
⎥
⎥⎦−4μoi9πa⎡⎢
⎢
⎢
⎢⎣(3a4)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦
=4μoiπa.14⎡⎢
⎢⎣1√14+116−4μoi9πa.34⎡⎢
⎢⎣1√14+916⎤⎥
⎥⎦
=4μoiπa[4√5]−μoi3πa[4√13][4√13]along
=4μoi2πa[1√5−13√13]along=2πoiπa[1√5−13√13]along.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
Find the magnetic field at a point P on the perpendicular bisector of the current carrying conductor :-
View SolutionConsider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
View Solution
Knowledge Check
ABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
 Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loop
Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loopPQRS is a square loop of a conducting wire. A current I enters the loop at Pand leaves the loop at S. The magnitude of magnetic field at the centre o of the square is
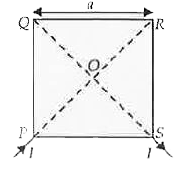 Aμ04π2√2IaBμ04π4√2IaCμ04π4√2IaDzero
Aμ04π2√2IaBμ04π4√2IaCμ04π4√2IaDzeroTwo charges 10μCand−10μC are placed at points A.andB separated by a distance of 10 cm. Find the electric field at a point P on the perpendicular bisector of AB at. a distance of 12 cm from its middle point.
A4.1×106N/CB2.2×106N/CC4.1×105N/CD2.2×105N/C
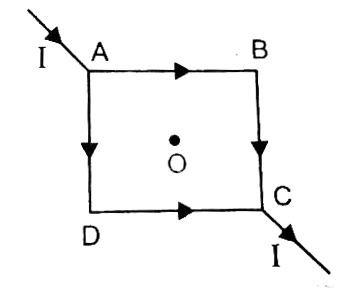
Figure shows a square loop made from a uniform wire. If a battery is connected between the pionts A and C. What will be the magnetic field at the centre O of the square?
View SolutionFind magnetic field at point P shown in Fig. point P is on the bisector of angle between the wires.
View SolutionFigure shows a square loop made from a uniform
wire. Find the magnetic field at the centre of the square
if a battery is connected between the points A and C.

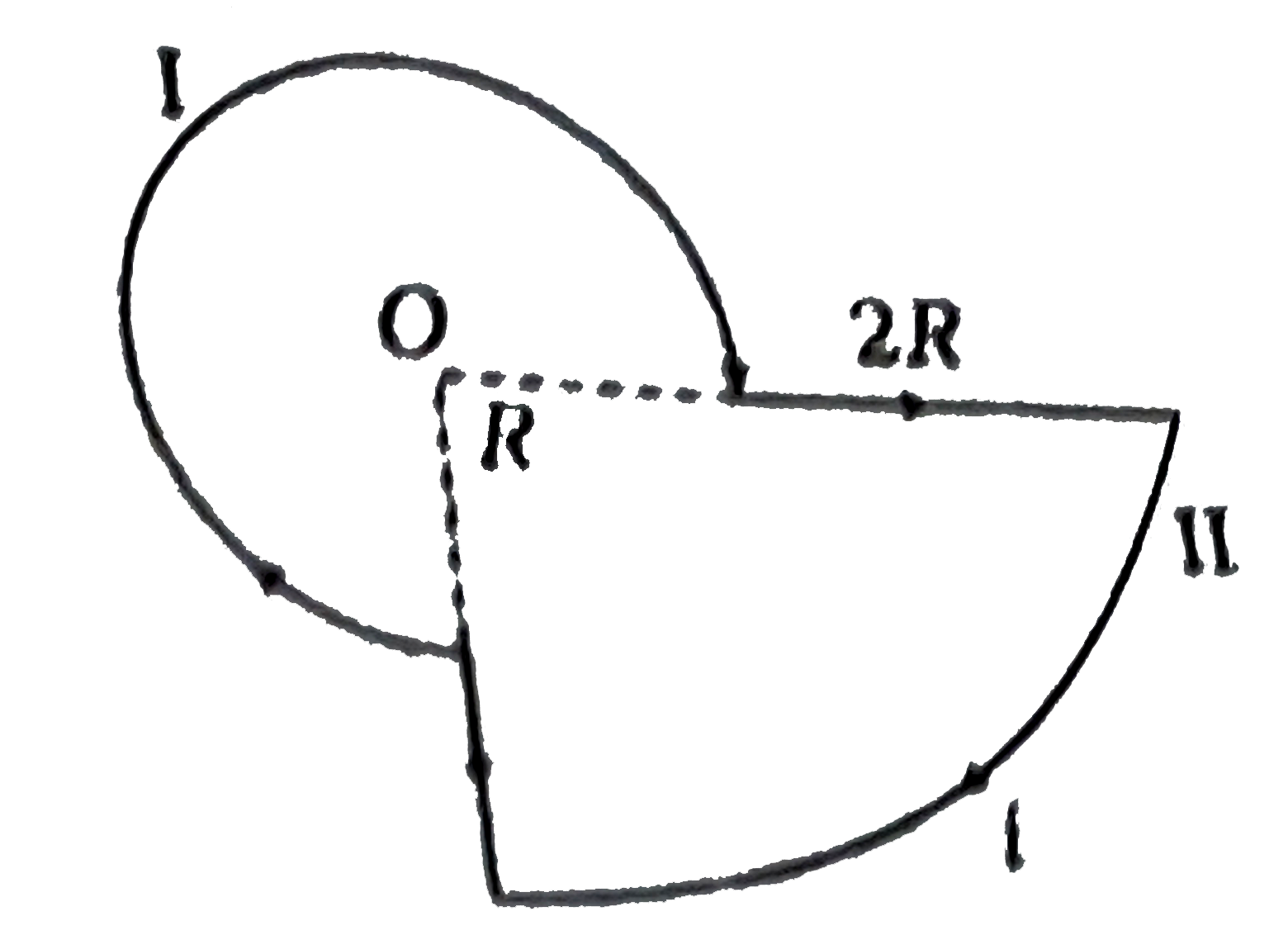
View SolutionIn the figure, the current l enters the circular loop of uniform wire of radius r at A and leaves it at B. The magnetic field of the centre of circular loop is

View SolutionConsider the circular loop having current I and with central point O. the magnetic field at the central point O is
View Solution
