Figure shows a string of linear mass density 1.0gcm−1 on which a wave pulse is travelling. Find the time taken by pulse in travelling through a distance of 50cm on the string. Take g=10ms−2
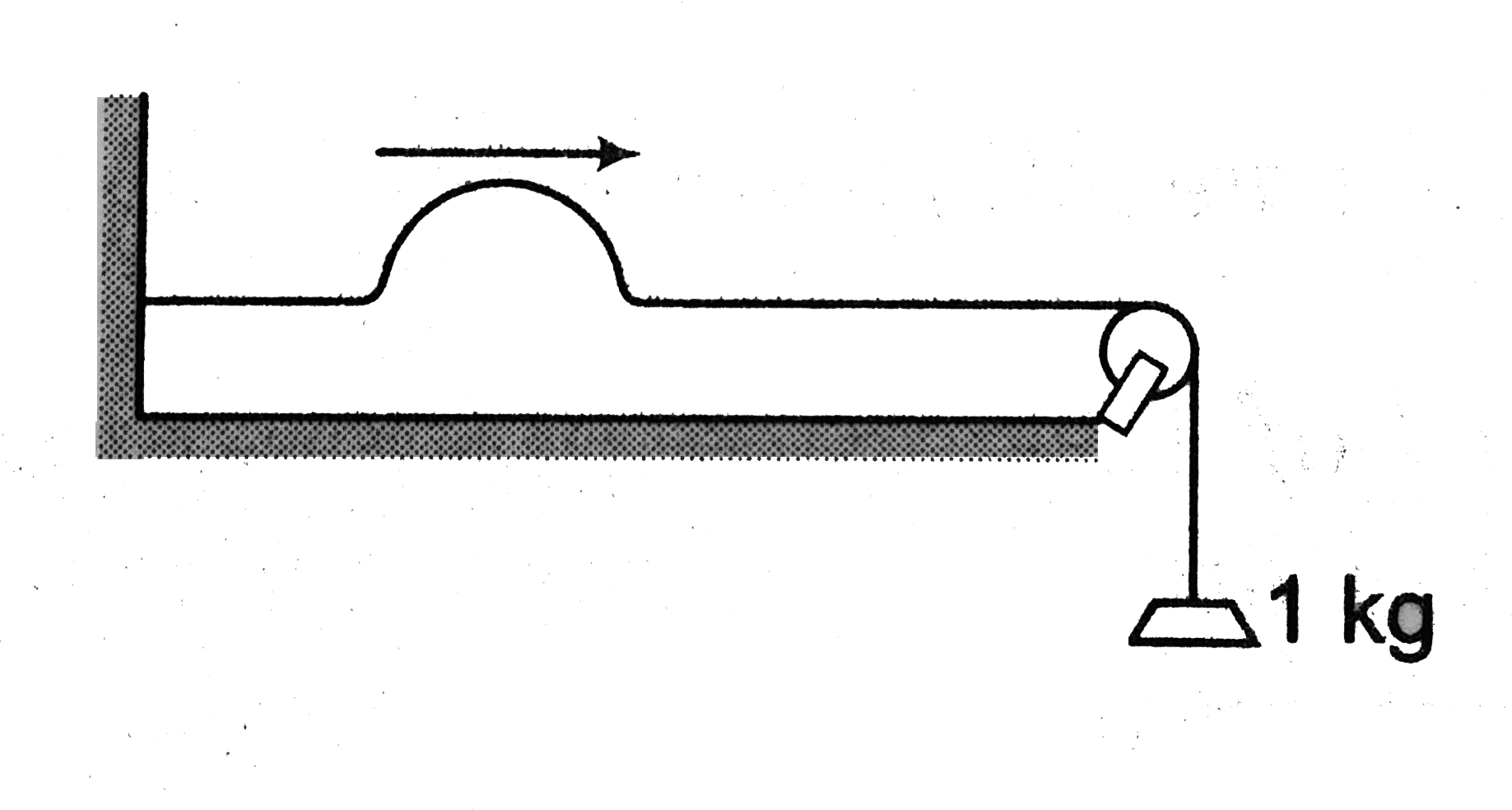
The tension in the string is F=mg=10N. The mass per unit length is
μ=1.0gcm−1=0.1kgm−1. The wave velocity is, therefore, v=√Fμ=√10N0.1kgm−1=10ms−1. The time taken by the pulse in travelling through 50cm is, therefore 0.05s.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Exercise 17.6
6 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Exercise 17.4
2 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
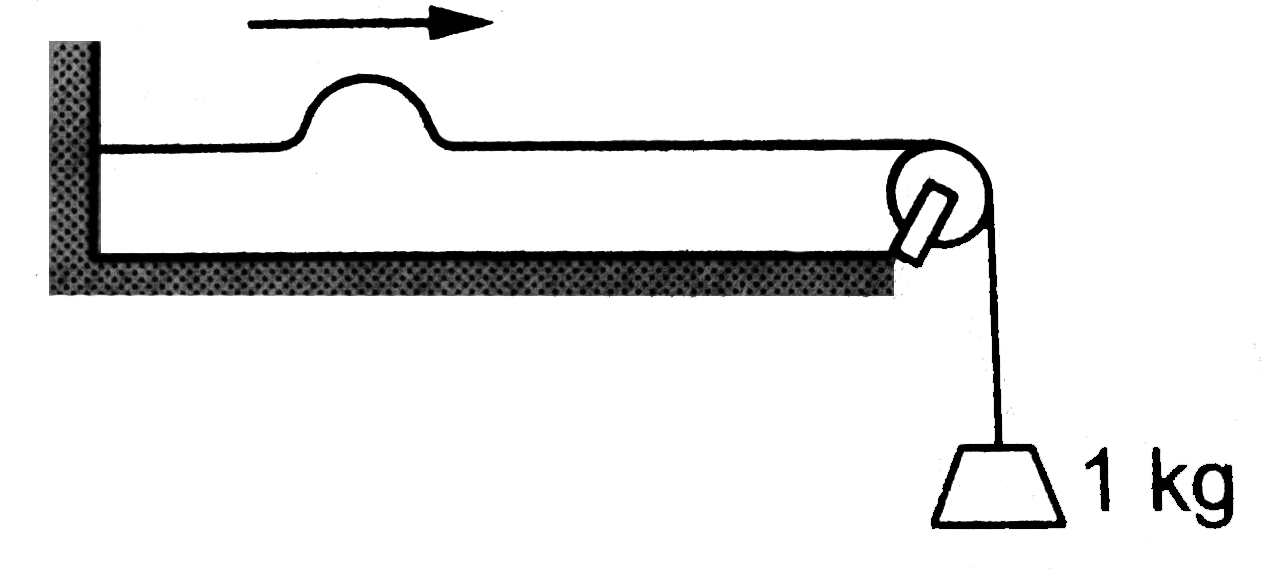
Figure showa a string of linear mass density 1.0gcm−1onwhichawaveps–eistravell∈g.F∈dthetimetakenbytheps–e∈travell∈gthroughadistanceof50cmonthestr∈g.Takeg=10 ms^-2.
View SolutionA way pulse is travelling on a string of linear mass density 6.4×10−3kgm−1 under a load of 80kgf. Calculate the time taken by the pulse to traverse the string, if its length is 0.7m.
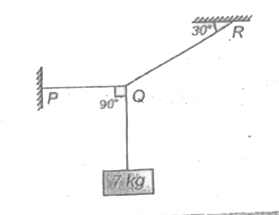
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure [ Take g =10m/s2]

View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
View SolutionAn harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubled
View SolutionCalculate the tension in the string shown in the figure. All the surfaces are frictionless. (Take g=10/ms−1)

View SolutionThe speed of a wave in a streched string is 20ms−1 and its frequency is 50 Hz. Calculate the phase difference in radian between two points situated at a distance of 10 cm on the string.
View SolutionA 4.0 kg block is suspended from the ceiling of an elevator through a string having a linear mass desity of 19.2×10−3kgm−1. Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elavator accelerates up at the rate of 2.0ms−2.Takeg=10ms−2.
View SolutionA harmonic wave has been set up on a very long string which travels along the length of string. The wave has frequency of 50 Hz. Amplitude 1 cm and wavelength 0.5 m. for the above described wave.
Statement (i): time taken by a point on the string to travel a distance of 8 m along the length of string is 0.32 s.
Statement (ii): time taken by a point in the string to travel a distance of 8m, once the wave has reached at that point and sets it into motion is 0.32 s.
View SolutionA uniform string of length 20m is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the support is :
(take g=10ms−2)
View Solution
