Figure shows, in cross section , two solid spheres with uniformly distributed charge throughout their volumes. Each has radius R. Point P lies on a line connecting the centers of the spheres, at radial distance R/2 from the center of sphere 1. If the net electric field at point P is zero, and Q1is64μC and Q2=8xμC, what is the value of x.
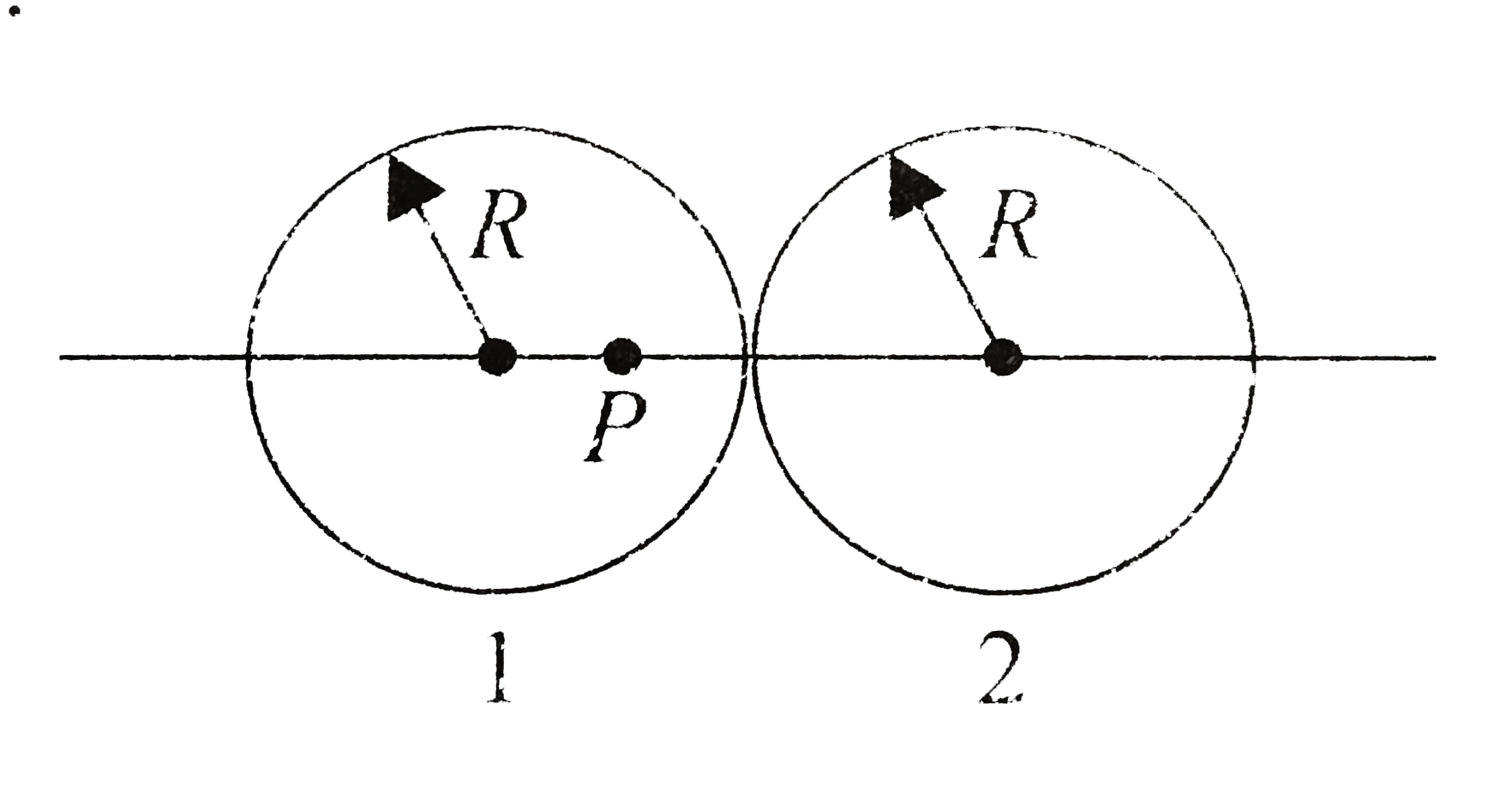
EP=kQ2(3R2)2−kQ1R2R3=0
or 49Q2=Q12 or Q2Q1=98
∴Q2=9×648=72μC=8×9μC
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks
10 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False Type
5 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
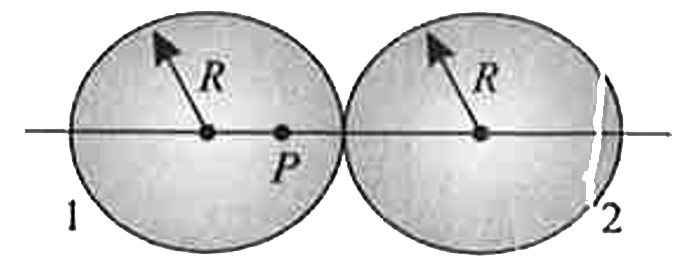
figure shows, in cross section, two solid spheres with uniformaly distributed charge throughout their volumes. Each has radius R. point P lies on a line connecting the centres of the spheres, at radial distance r/2.00 from the centre of sphere 1 . If the net electric field at point P is zero what is the ratio q2/q1 of the total charges ?
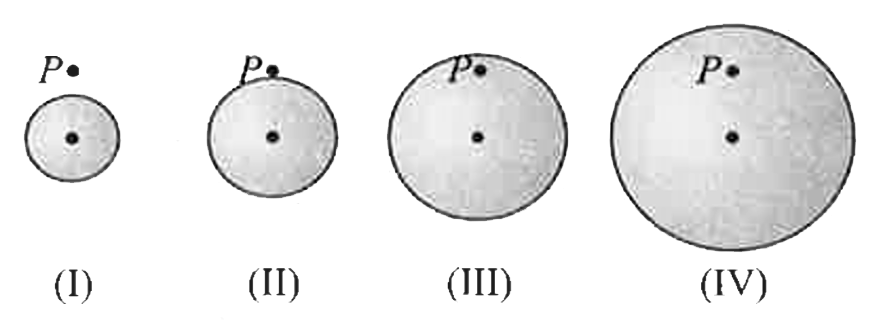
View SolutionFigure showns four solid spheres, each with charge Q uniformly distributed through its volume. The figure also shows a point P for each sphere. All at the same distance from the centre of the sphere. Rank the spheres according to the magnitude of the electric field they produce at point P.
View Solution
Knowledge Check
There is a solid sphere of radius R having uniformly distributed charge throughout it. What is the relation between electric field E and distance r from the centre (r is less than R) ?
AE∝r−2BE∝r−1CE∝rDE∝r2Let ρ(r)=QrπR4 be the charge density distribution for a soild sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
AQr214πε0R4BQr213πε0R4C0DQ4iε0r21
Figure shows a solid hemisphere with a charge of 5 nC distributed uniformly through its volume. The hemisphere lies on a plane and point P is located on the plane, along a radial line from the centre of curvature at distance 15 cm. The electric potential at point P due to the hemisphere is:

View SolutionA positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r(r>R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R/2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.

View SolutionLet P(r)=QπR4r be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance r1 from the centre of the sphere, the magnitude of electric field is:
View SolutionA solid sphere of radius R is charged uniformly through out the volume. At what distance from its surface is the electric potential 1/4 of the potential at the centre?
View SolutionA sphere of radius R has a uniform distribution of electric charge in its volume. At a distance x from its centre, for x<R, the electric field is directly proportional to
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View Solution
