Figure shows tow blocks A and B, each having a mass of 320 g connected by a light string passing over a smooth light puley. The horizontal surface on which the block A can slide is smooth. The blcok A is attached to a spring of lconstant 40 N/m whose other end is fixed to a support 40 cm the horizontal surface. Initially, the sprng is vertical and unstretched when the system is released to move. Find the velocity of theh block A at teh instnt it breaks of the surface below it. Take g=10ms2.
The correct Answer is:A
m=320g=0.32kg,k=40Nm
h=40cm=0.4m,g=10msec2
From the free body diagram,
kxcosθ=mg
(when the block breaks of R=0)<br>rarr costheta=(mg)/(kx)<br>rarr 0.4/(0.4+x=3.2/(40x)<br>rarr 16x=3.2x+1.28<br>rarr x=0.1m<br>So,s=AB=sqrt((h+x^2)-h^2)<br>=sqrt((0.5)^2-(0.4)^2)=0.3m
Let the velocity of tebody at B be v change in K.E. work done (for the system)
(12μ2+12mv2)=−12kx2+mgs
→(0.32)×v2
=−(12)×40×(1.0)2+(0.2)×10×(0.3)
→v=1.5msec
Fromtheure<br>/_\l=h(sectheta-1)........i<br>Fromthee≠rgyconservation<br>mgs=2[1/2mv^2]+1/2K/_\l^2<br> mgh than theta =mv^2+1/2kh^2(sectheta-1)^2.....ii<br>Fromthelawofmotionatbreakof<br>mgkh(sectheta-1)costheta<br>rarr 1-costheta=mg/kh<br>rarr costheta=1-mg/kh<br>or costheta=(kh-mg)/kh<br>orcostheta=(kh-mg)/kh<br>=(40xx0.4-0.32xx10)/(40xx0.4)<br>=0.8<br>Pu∈gthevalueoftheta∈equationi,<br>0.32xx10xx0.4xx0.75<br>=0.32v^2+1/240xx(0.4)^2(1.25-1)^2<br>rarr 0.96=0.32v^2+0.2<br>rarr 0.32v2=0.72
rarr v=1.5m/sec
Topper's Solved these Questions
Similar Questions
Figure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .
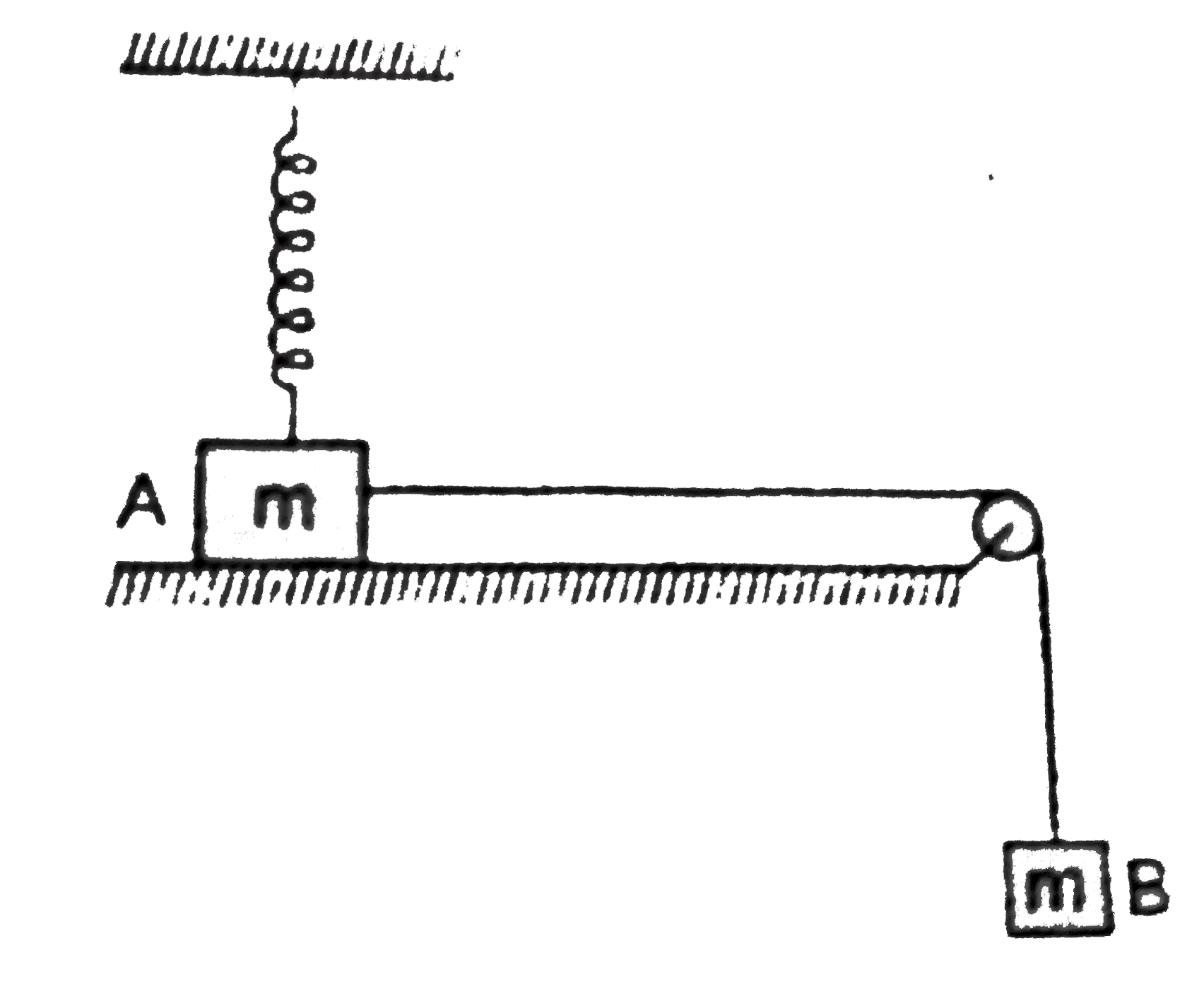
View SolutionFigure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .

View Solution
Knowledge Check
Figure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .
 A√198B√32C√94DNone of these
A√198B√32C√94DNone of theseTwo blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
A50N up the planeB50N down the planeC100N up the planeD100N down the planeFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.
 AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
The tension in the string connected between blocks is

View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
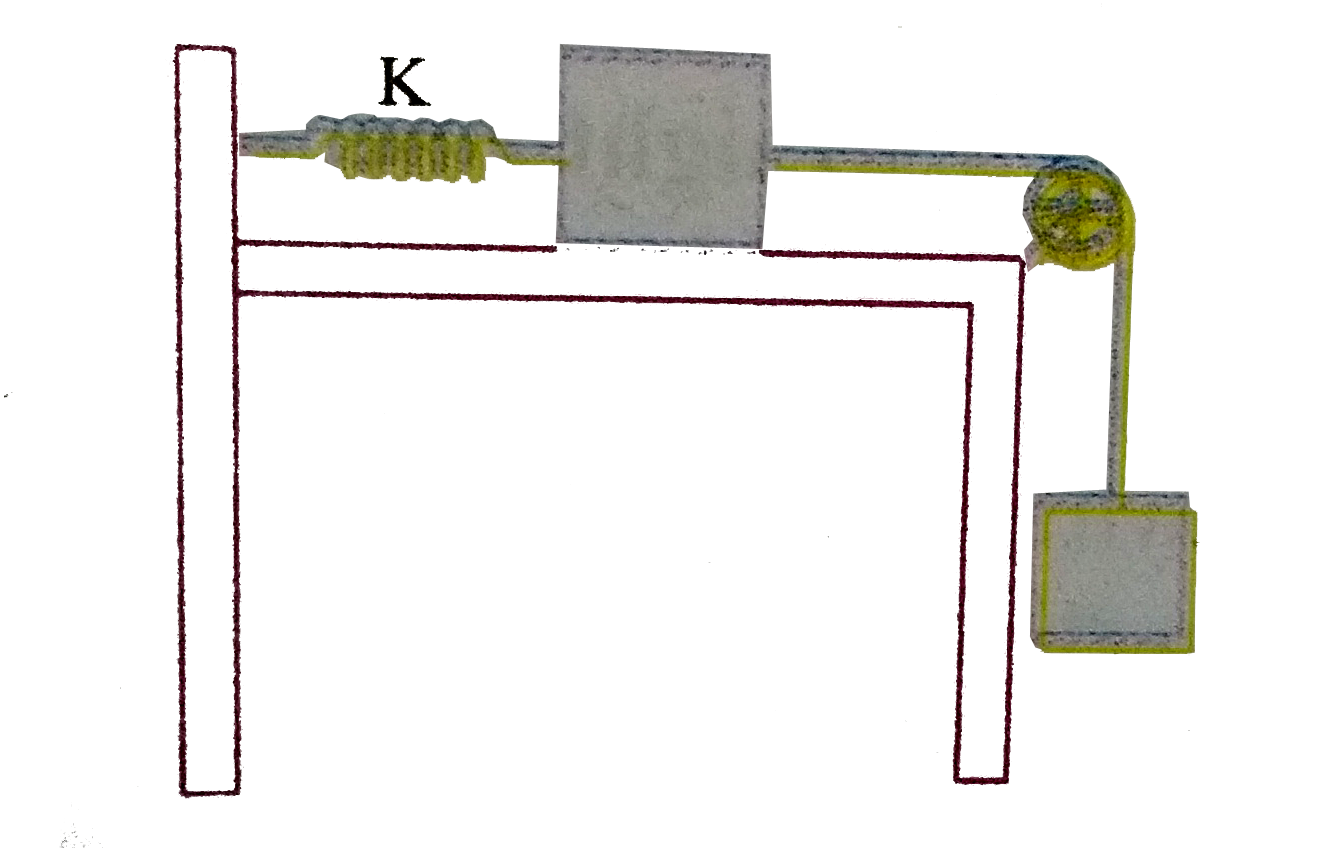 .
.
View SolutionTwo blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
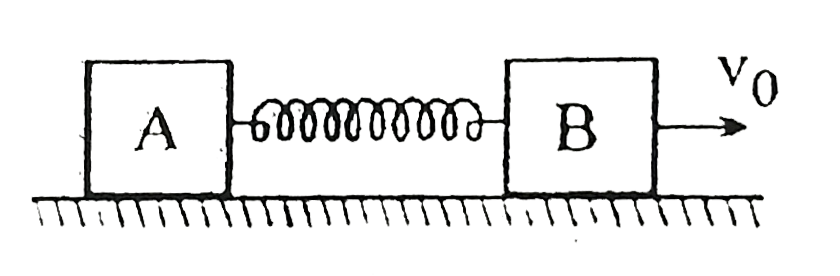
View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View Solution
