Find aC and α of the smooth rod of mass m and length l.
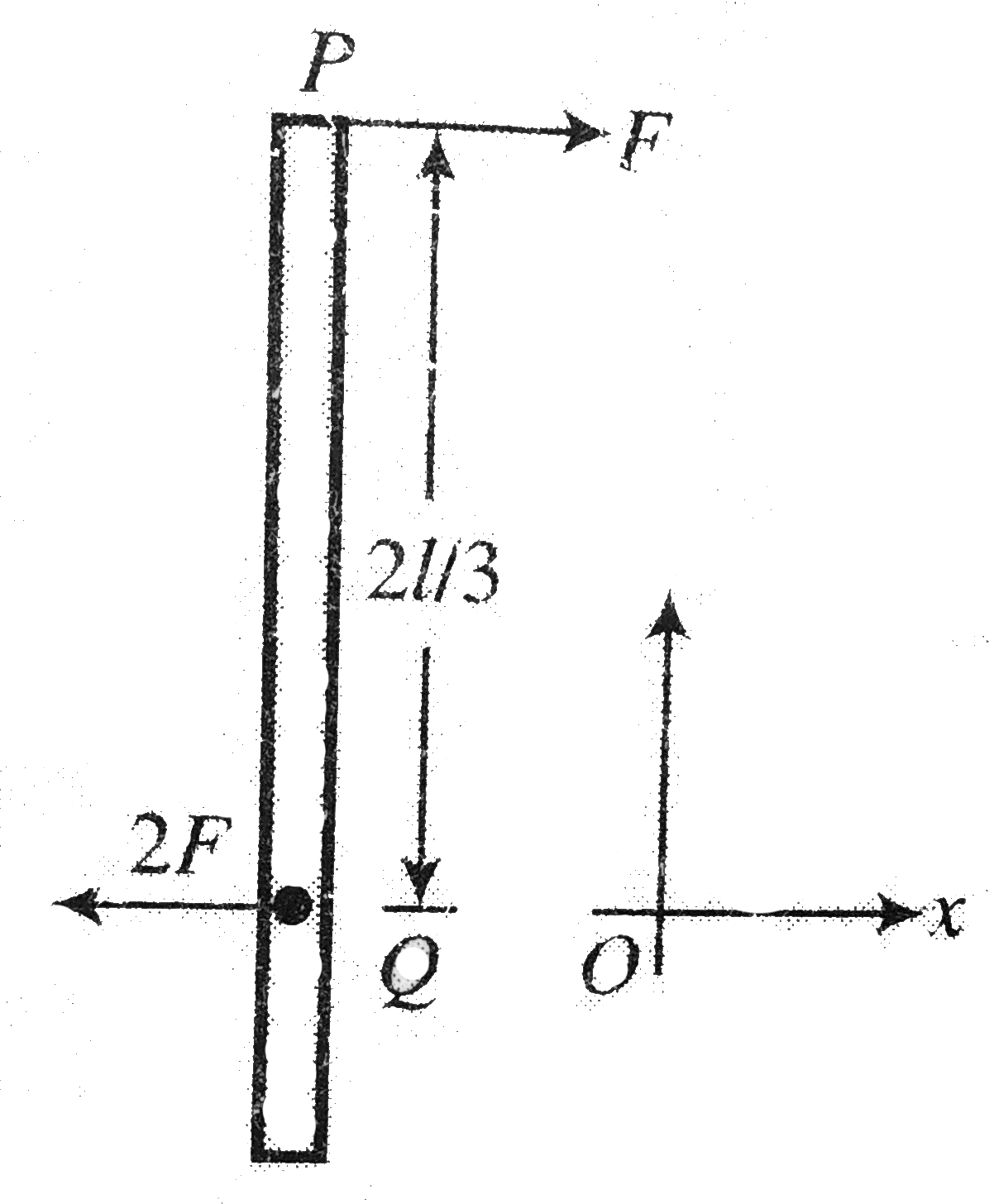
Force equation
F−2F=ma⇒a=−Fm
Hence →a=−Fmˆi
Torque equation about centre of mass
F.l2+(23−l2)=lCα
F.l2+Fl6=ml212.α
32Fl=ml212.α⇒8Fml
Hence →α=(8F).(ml)ˆk
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct
97 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.3
15 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
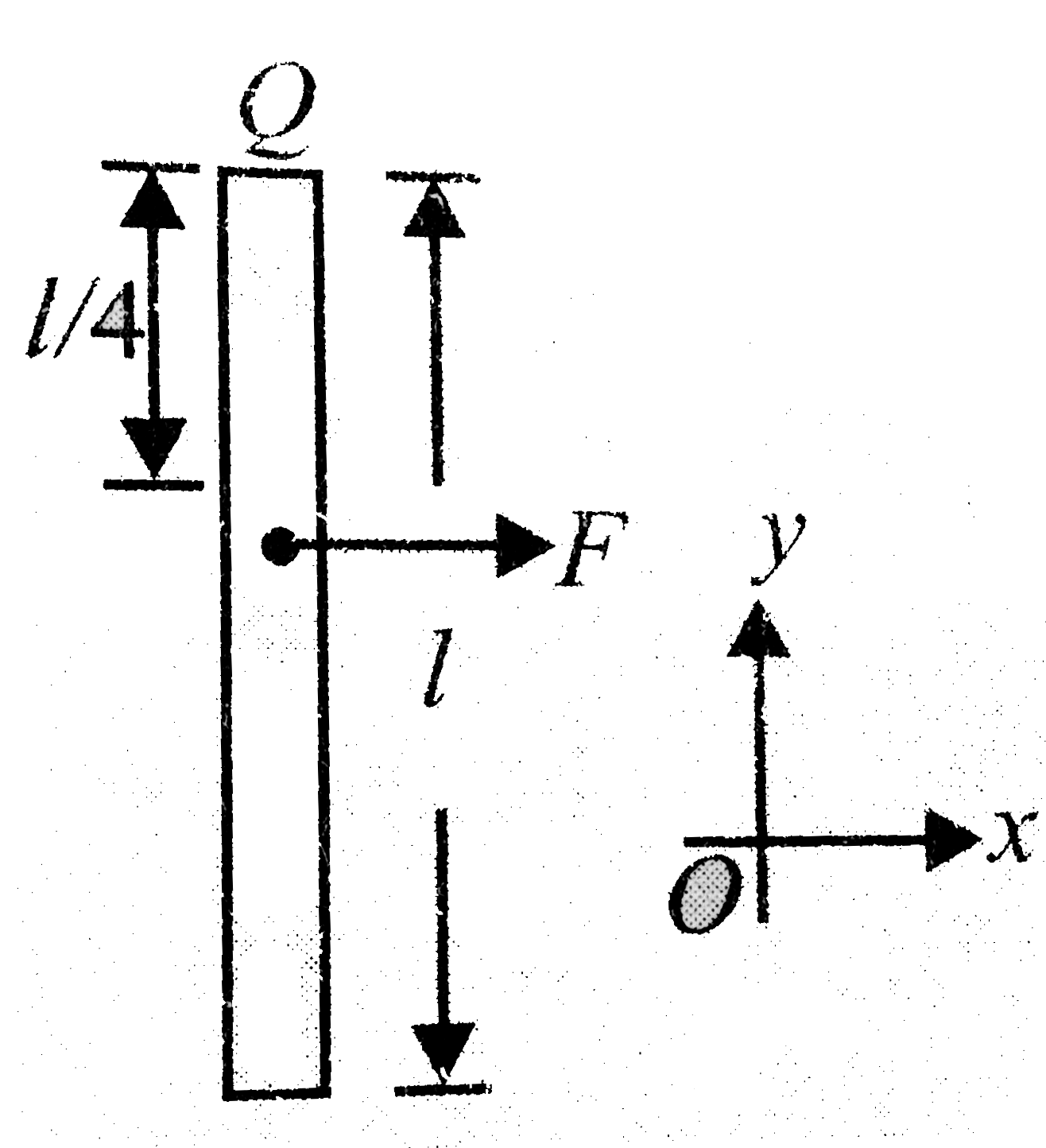 Find α,aQ and the point of zero acceleration when the horizontal force F acts on the smooth rod of mass m and length l which is kept on a horizontal surface.
Find α,aQ and the point of zero acceleration when the horizontal force F acts on the smooth rod of mass m and length l which is kept on a horizontal surface.
View SolutionA ball of mass m collides elastically with a smooth hanging rod of mass M and length l.
a. If M=3m find the value of b for which no horizontal reaction occurs at the pivot.
b. For what value of m/M the ball falls dead just after the collision assuminng e=(12)?

View Solutionfind the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its ends and perpendicular to its length.
View SolutionABC is a triangular framwork of three uniform rods each of mass m and length 2l. It is free to rotate in its own plane about a smooth horizontal axis through A which is perpendicular to ABC. If it is released from rest when AB is horizontal and C is above AB. Find the maximum velocity of C in the subsequent motion.
View SolutionThe radius of gyration of a uniform rod of mass m and length l about an axis perpendicular to its length and at distance l4 from its centre will be
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionMoment of inertia of a uniform rod of mass m and length l is 712ml2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionCalculate the force exerted by point mass m on rod of uniformly distributed mass M and length l (Placed as shown in figure)
 .
.
View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.

View Solution
