Find the moment of inertia of the two uniform joint rods about point P as shown in Fig. Use parallel axis theorem. Mass of each rod is M.
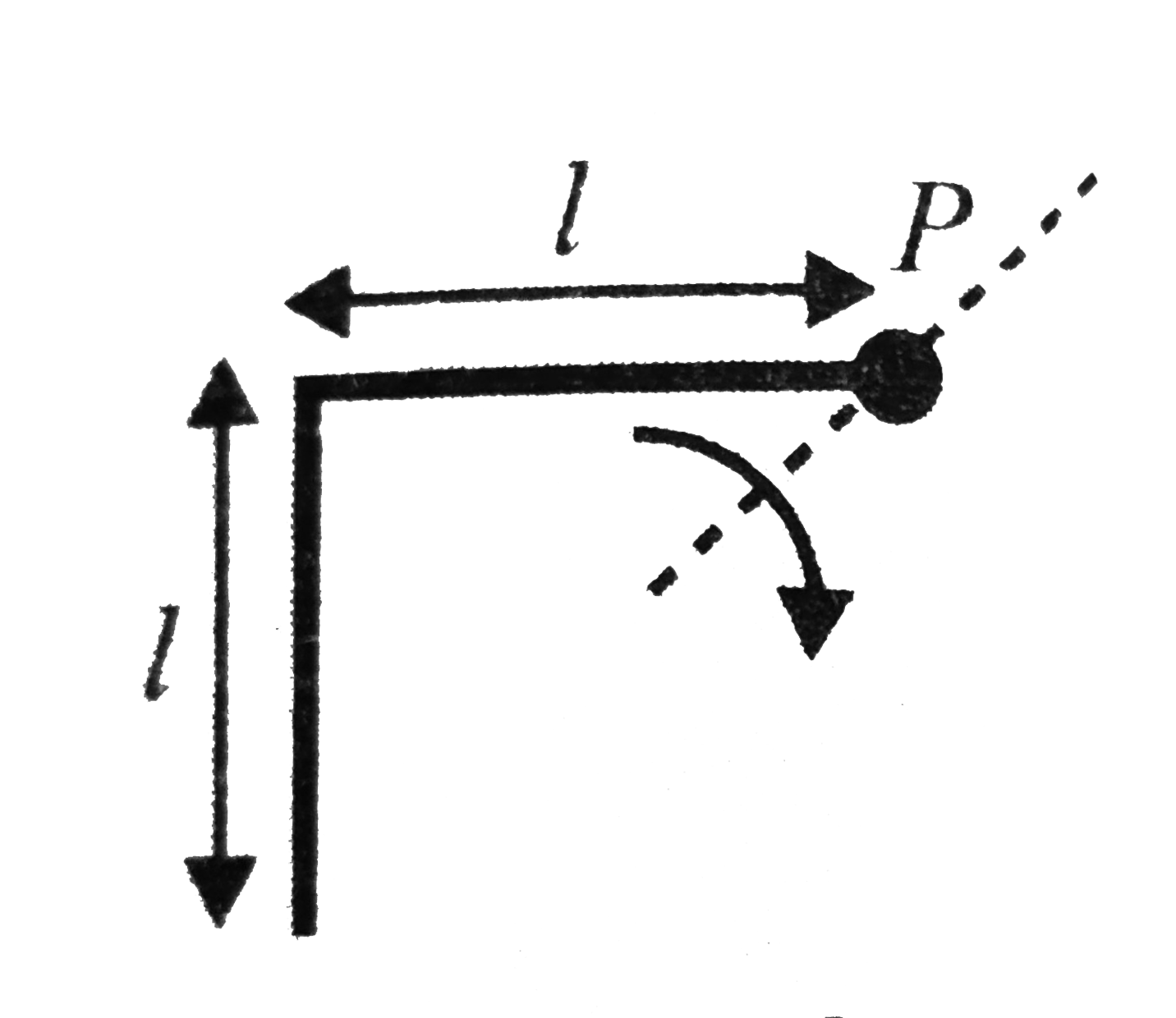
IP=IP1+IP2
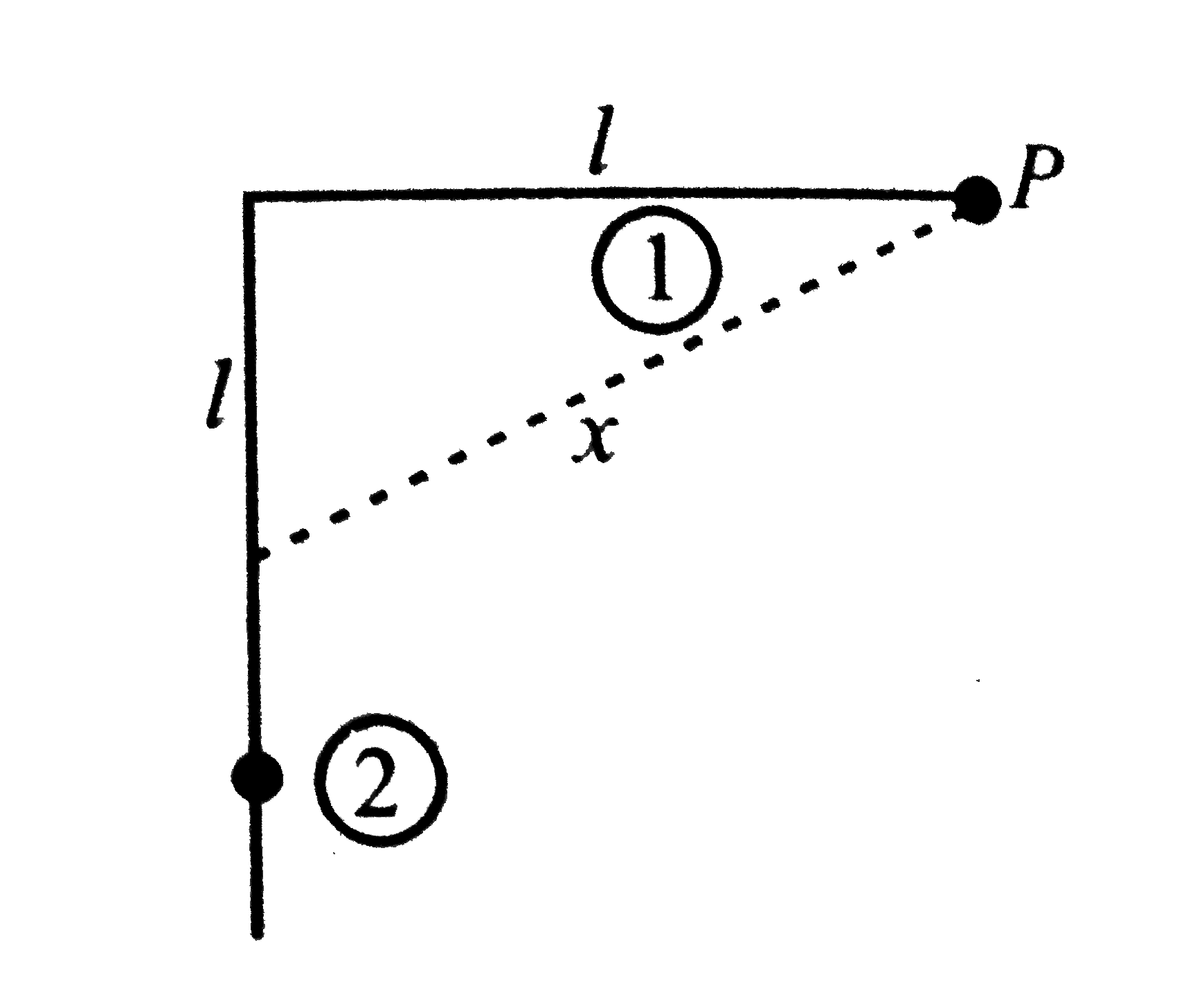
IP=Ml23+(Ml212+Mx2)
x2=l2+(l2)2=5l24
⇒lP=Ml23+[Ml212+M(5l24)]=53Ml2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.3
15 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.4
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Knowledge Check
The moment of inertia of a system of four rods each of length l and mass m about the axis shown is
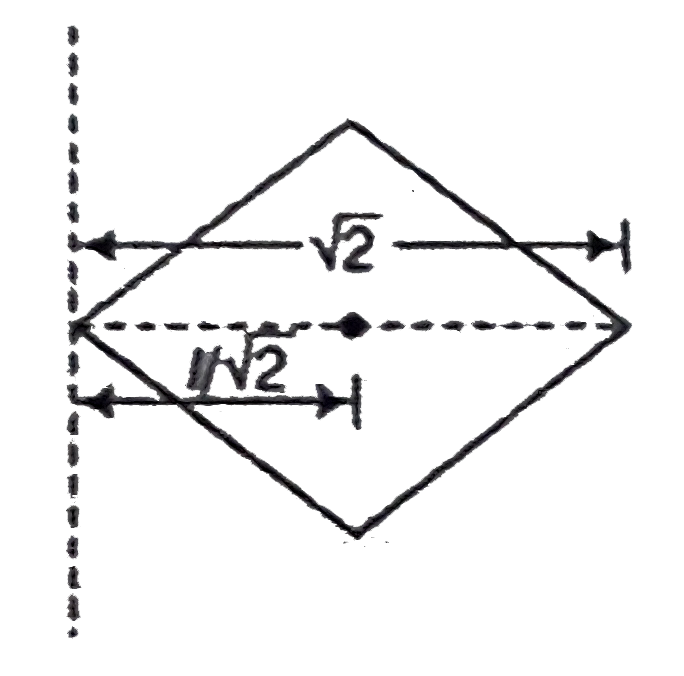 A23ml2B2ml2C3 ml2D83ml2
A23ml2B2ml2C3 ml2D83ml2A uniform rod of mass 2M is bent into four adjacent semicircles each of radius r, all lying in the same plane. The moment of inertia of the bent rod about an axis through one end A and perpendicular to plane of rod is
 A22Mr2B88Mr2C44Mr2D66Mr2
A22Mr2B88Mr2C44Mr2D66Mr2
Find the moment of inertia of a thin uniform rod about an axis perpendicular to its length and passing through a point which is at a distance of 13 from one end. Also find radius of gyration about that axis.
View SolutionFind the M.I. of thin uniform rod of mass M and length L about the axis as shown.
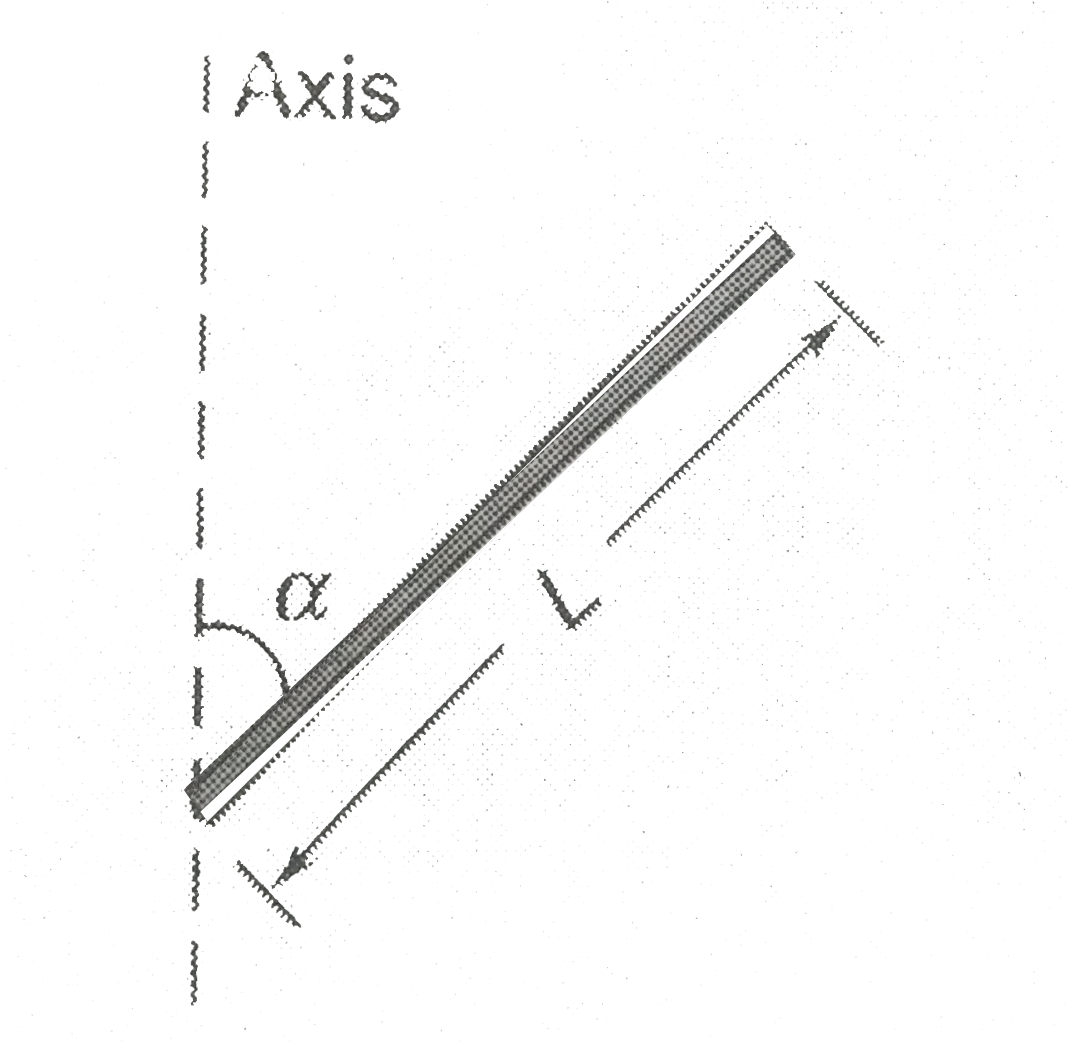
View SolutionCalculate the moment of inertia of a rectangular frame formed by uniform rods having mass m each as shown in about an axis passing through its centre and perpendicular to the plane of frame. Also find moment of inertia about an axis passing through PQ ?

View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
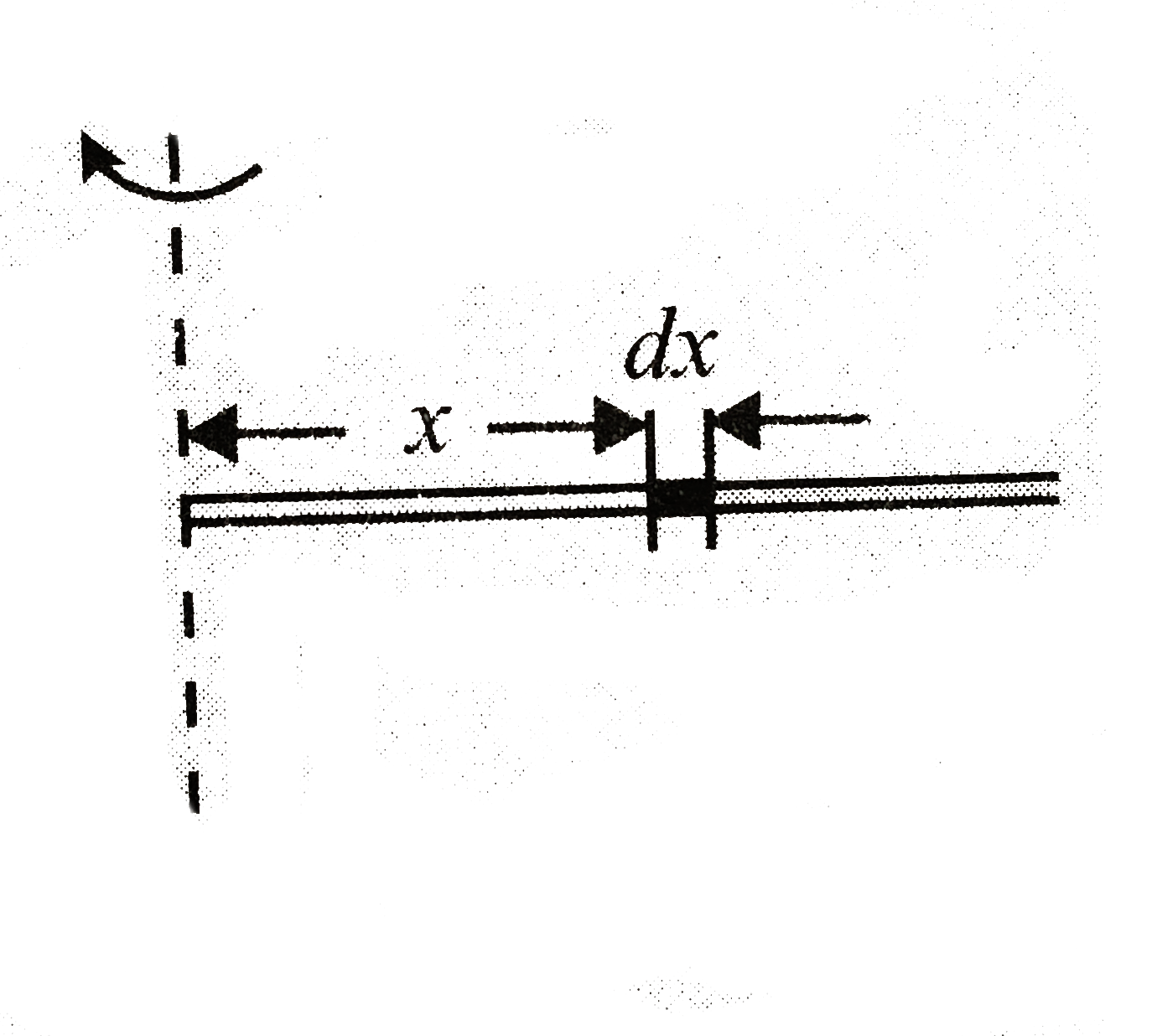
View Solution

