Find the potential energy of 4-particles, each of mass 1 kg placed at the four vertices of a square of side length 1 m.
+4.0G
7.5G
−5.4G
+6.3G
The correct Answer is:C
To find the potential energy of four particles, each of mass 1 kg, placed at the vertices of a square with a side length of 1 m, we can follow these steps:
Step 1: Understand the Configuration
We have four particles, each of mass m=1kg, located at the vertices of a square. Let's label the vertices as A, B, C, and D. The distance between adjacent vertices (e.g., A and B) is the side length of the square, which is 1m.
Step 2: Calculate the Distances
The distances between the particles are as follows:
- Distance between adjacent vertices (e.g., A and B): rAB=1m
- Distance between opposite vertices (e.g., A and C): rAC=√2m (using Pythagorean theorem)
Step 3: Write the Formula for Gravitational Potential Energy
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
where G is the gravitational constant, G≈6.674×10−11N m2/kg2.
Step 4: Calculate the Potential Energy Between Each Pair of Particles
We need to consider the potential energy between each pair of particles:
1. Between A and B:
UAB=−G⋅1⋅11=−G
2. Between B and C:
UBC=−G⋅1⋅11=−G
3. Between C and D:
UCD=−G⋅1⋅11=−G
4. Between D and A:
UDA=−G⋅1⋅11=−G
5. Between A and C:
UAC=−G⋅1⋅1√2=−G√2
6. Between B and D:
UBD=−G⋅1⋅1√2=−G√2
Step 5: Sum the Potential Energies
Now, we sum all the potential energies:
Utotal=UAB+UBC+UCD+UDA+UAC+UBD
Substituting the values:
Utotal=−G−G−G−G−G√2−G√2
Utotal=−4G−2G√2=−4G−√2G
Step 6: Final Expression
Thus, the total gravitational potential energy of the system is:
Utotal=−(4+√2)G
We have four particles, each of mass m=1kg, located at the vertices of a square. Let's label the vertices as A, B, C, and D. The distance between adjacent vertices (e.g., A and B) is the side length of the square, which is 1m.
The distances between the particles are as follows:
- Distance between adjacent vertices (e.g., A and B): rAB=1m
- Distance between opposite vertices (e.g., A and C): rAC=√2m (using Pythagorean theorem)
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
where G is the gravitational constant, G≈6.674×10−11N m2/kg2.
We need to consider the potential energy between each pair of particles:
1. Between A and B:
UAB=−G⋅1⋅11=−G
2. Between B and C:
UBC=−G⋅1⋅11=−G
3. Between C and D:
UCD=−G⋅1⋅11=−G
4. Between D and A:
UDA=−G⋅1⋅11=−G
5. Between A and C:
UAC=−G⋅1⋅1√2=−G√2
6. Between B and D:
UBD=−G⋅1⋅1√2=−G√2
Now, we sum all the potential energies:
Utotal=UAB+UBC+UCD+UDA+UAC+UBD
Substituting the values:
Utotal=−G−G−G−G−G√2−G√2
Utotal=−4G−2G√2=−4G−√2G
Thus, the total gravitational potential energy of the system is:
Utotal=−(4+√2)G
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.5
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.3
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Find the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
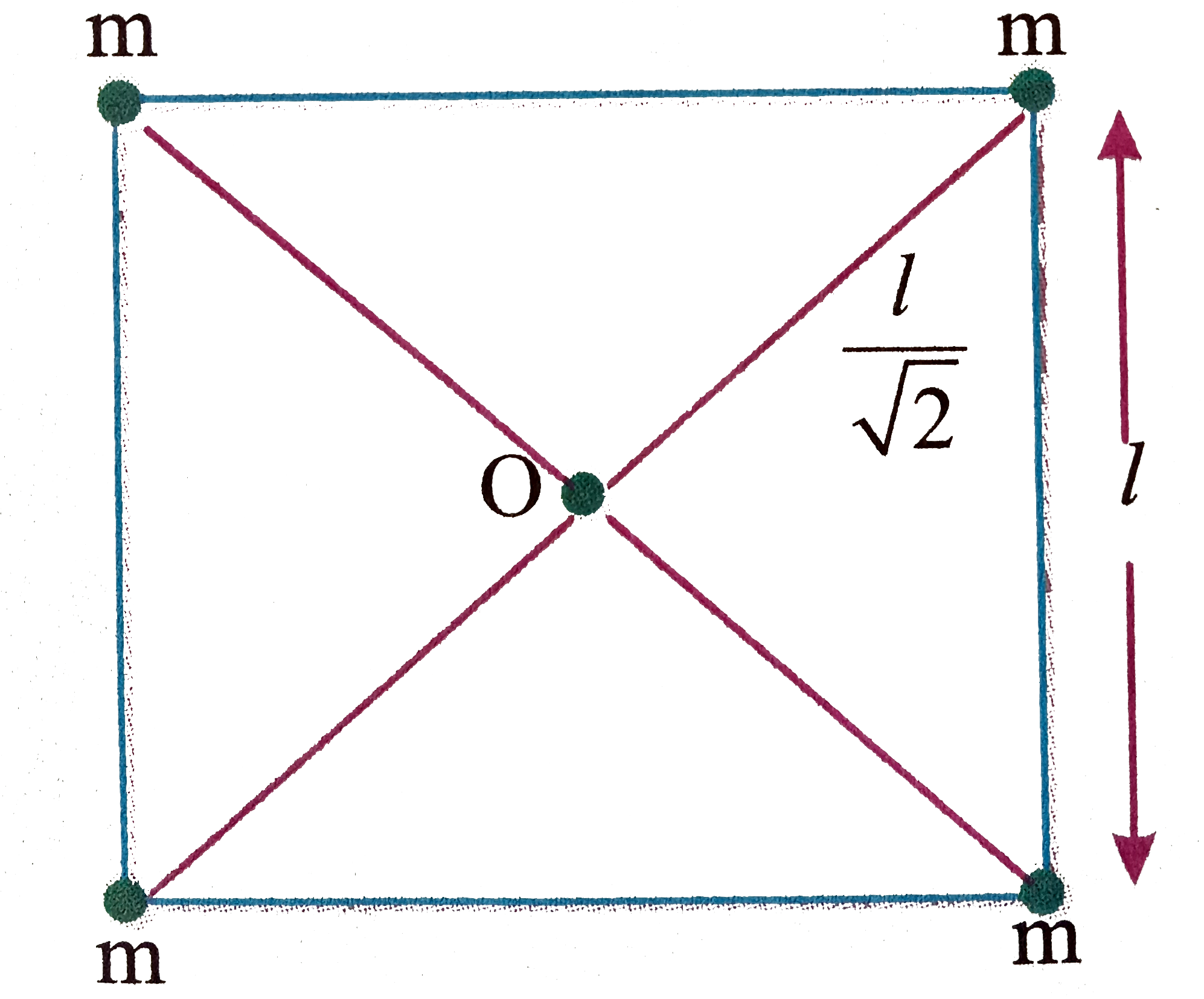
View SolutionFind the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
View Solution
Knowledge Check
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−√2Gm2l(2−1√2)B−2Gm2l(2+1√2)C−√2Gm2l(√2−1√2)D−2Gm2l(√2−1√2)
Find the potential energy of a system of eight particles of mass M placed at the vertices of a cube of side L. neglect the self energy of the particles.
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the
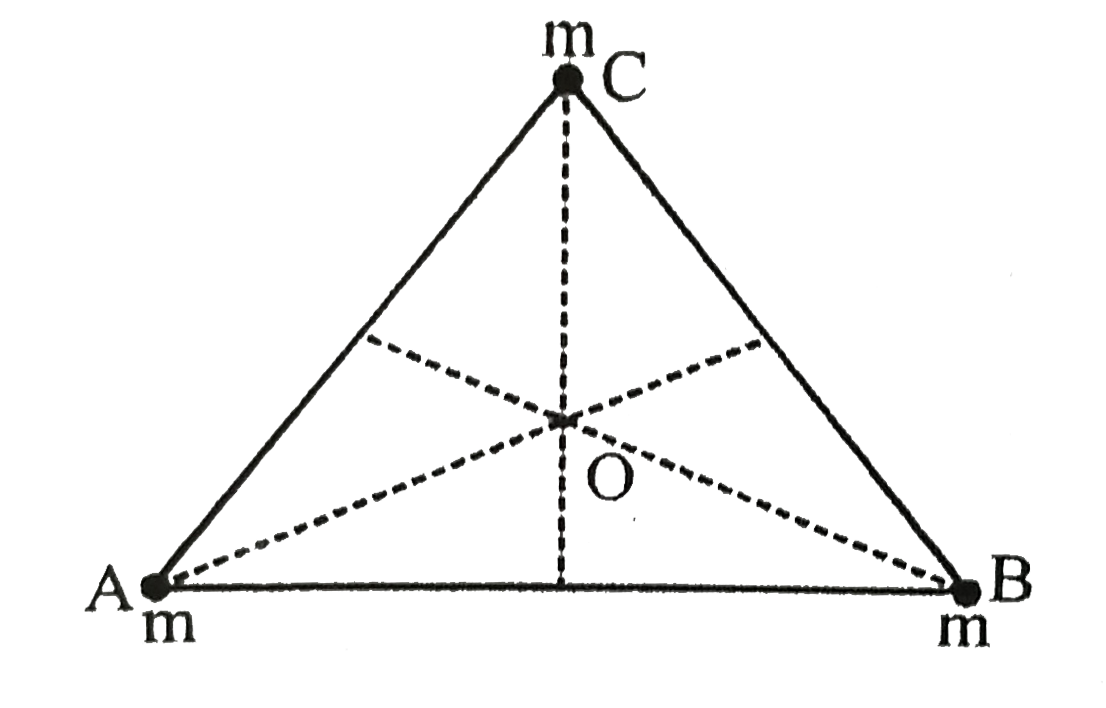
(a) the mid point of a side
(b) centre of the triangle
View SolutionFind the potential energy of a system of 3 particles kept at the vertices of an equilateral triangle of side r.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A,B,C and D of a square of side 1m. Find square of distance of their centre of mass from A.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View Solution
