Find the radius of gyration of a circular ring of radius r about a line perpendicular to the plane of the ring and passing through one of this particles.
The correct Answer is:B
To find the radius of gyration of a circular ring of radius r about a line perpendicular to the plane of the ring and passing through one of its particles, we can follow these steps:
Step 1: Understand the Setup
We have a circular ring with a radius r and a mass m. The line about which we want to find the radius of gyration is perpendicular to the plane of the ring and passes through one of the particles on the ring.
Step 2: Identify the Moment of Inertia
The moment of inertia I about the line xy can be expressed in terms of the radius of gyration kxy using the formula:
Ixy=mk2xy
where kxy is the radius of gyration we want to find.
Step 3: Use the Parallel Axis Theorem
To find Ixy, we can use the parallel axis theorem. The theorem states:
Ixy=Iab+md2
where:
- Iab is the moment of inertia about an axis through the center of mass (CM) of the ring.
- d is the distance between the two axes.
In this case, the distance d is equal to the radius r of the ring since the line xy is perpendicular to the plane of the ring and passes through one of its particles.
Step 4: Calculate the Moment of Inertia About the Center of Mass
The moment of inertia of a circular ring about an axis through its center (perpendicular to the plane) is given by:
Iab=mr2
Step 5: Substitute Values into the Parallel Axis Theorem
Substituting Iab and d into the parallel axis theorem:
Ixy=mr2+mr2=2mr2
Step 6: Relate Moment of Inertia to Radius of Gyration
Now we can relate this back to the radius of gyration:
mk2xy=2mr2
Dividing both sides by m:
k2xy=2r2
Step 7: Solve for the Radius of Gyration
Taking the square root of both sides gives:
kxy=√2r
Final Result
Thus, the radius of gyration of the circular ring about the specified line is:
kxy=√2r
---
We have a circular ring with a radius r and a mass m. The line about which we want to find the radius of gyration is perpendicular to the plane of the ring and passes through one of the particles on the ring.
The moment of inertia I about the line xy can be expressed in terms of the radius of gyration kxy using the formula:
Ixy=mk2xy
where kxy is the radius of gyration we want to find.
To find Ixy, we can use the parallel axis theorem. The theorem states:
Ixy=Iab+md2
where:
- Iab is the moment of inertia about an axis through the center of mass (CM) of the ring.
- d is the distance between the two axes.
The moment of inertia of a circular ring about an axis through its center (perpendicular to the plane) is given by:
Iab=mr2
Substituting Iab and d into the parallel axis theorem:
Ixy=mr2+mr2=2mr2
Now we can relate this back to the radius of gyration:
mk2xy=2mr2
Dividing both sides by m:
k2xy=2r2
Taking the square root of both sides gives:
kxy=√2r
Thus, the radius of gyration of the circular ring about the specified line is:
kxy=√2r
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -214videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
The moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
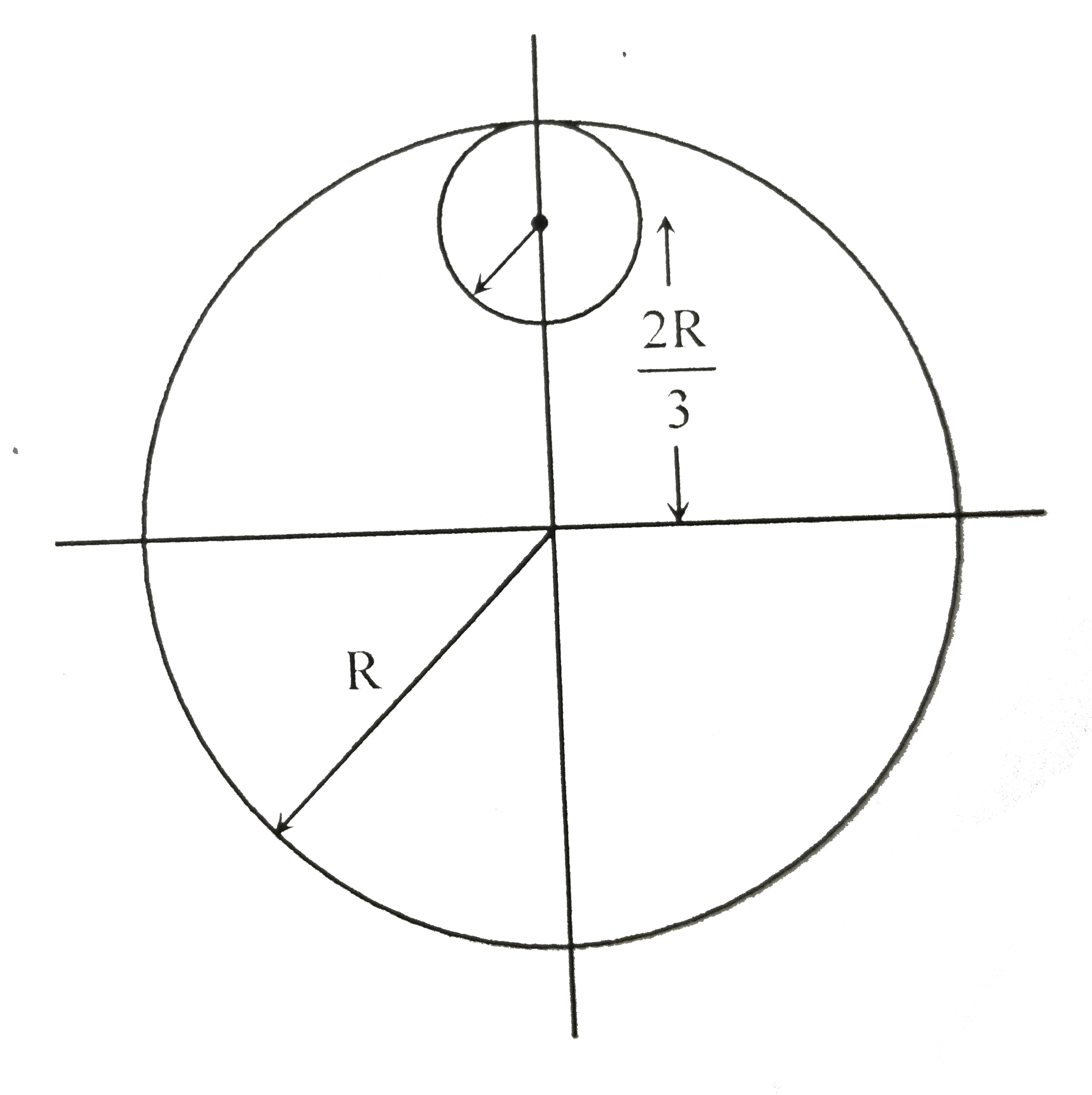 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
The radius of gyration of a uniform disc about a line perpendicular to the disc equals to its radius. Find the distance of the line from the centre.
View SolutionThe moment of inertia of a uniform semicircularwire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is :
View SolutionThe moment of inertia of a uniform semicircular wire of mass 'M' and radius 'r' about a line perpendicular to the plane of the wire through the center is
View SolutionThe radius of gyration of a uniform circular ring of radius R, about an axis which is a chord of circle of length √3R is ,
View SolutionThe radius of gyration of a uniform circular ring of radius R, about an axis which is a chord of circle of length √3R is ,
View SolutionThe M.I. of a ring of mass M and radius R about a tangential axis perpendicular to its plane is :
View SolutionThe radius of gyration of a uniform disc about a line perpendicular to the disc equals ilts radius. Find the distance of the line from the centre.
View Solution

