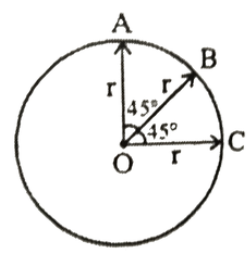
Find the resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure. Radius of the circle is R.

OA=OC<br>OA+OC is along OB (bisector ) and its magnitude is 2Rcos45∘=R√2
(OA+OC)+OB is along OB and its magnitude is R√2+R=R(1+√2)
Topper's Solved these Questions
- VECTORSBook:DC PANDEY ENGLISHChapter:VECTORSExercise:Exercise 5.1
Explore 5 Videos
- VECTORSBook:DC PANDEY ENGLISHChapter:VECTORSExercise:Exercise 5.2
Explore 4 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS Book:DC PANDEY ENGLISHChapter:UNITS, DIMENSIONS & ERROR ANALYSIS Exercise:Medical entrances gallery
Explore 32 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Integer Type Question
Explore 11 Videos
Similar Questions
The resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
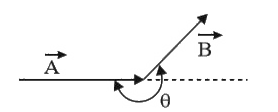
View SolutionWhat is the angle between the vector →A and →B as shown in figure ?
View SolutionThe resultant of vectors −−→OAand−−→OB is perpendicular to −−→OA. Find the angle AOB.
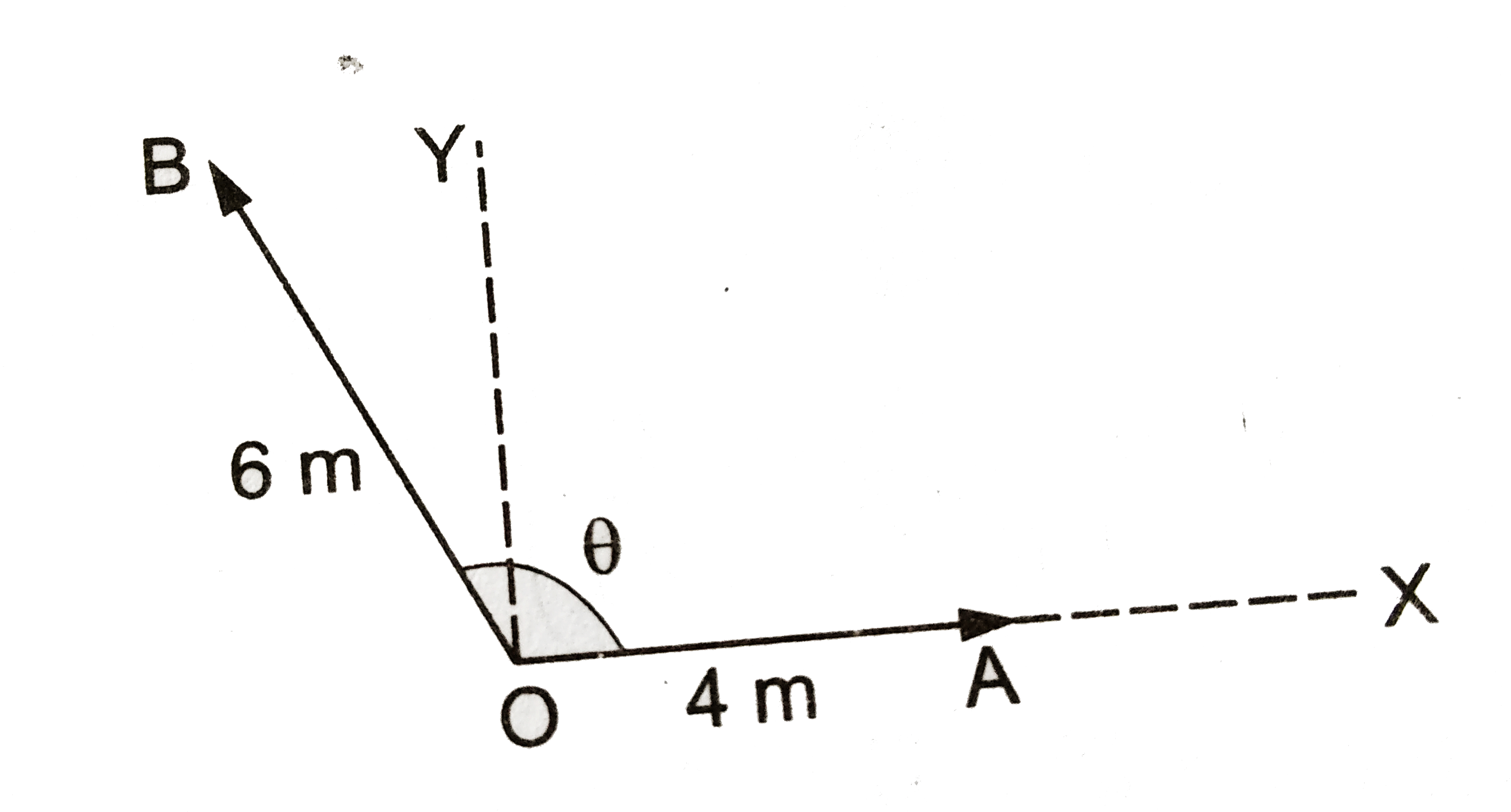
View SolutionThe resultant of vectors −−→OAand−−→OB is peerpendicular to −−→OA. Find the angle AOB.

View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionIf →A,→B and →C are three vectors, then the wrong relation is :
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is

View SolutionThe sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.

View SolutionABCD is a quadrilateral and E is the point of intersection of the lines joining the middle points of opposite side. Show that the resultant of −−→OA , −−→OB , −−→OC and −−→OD = 4 −−→OE , where O is any point.
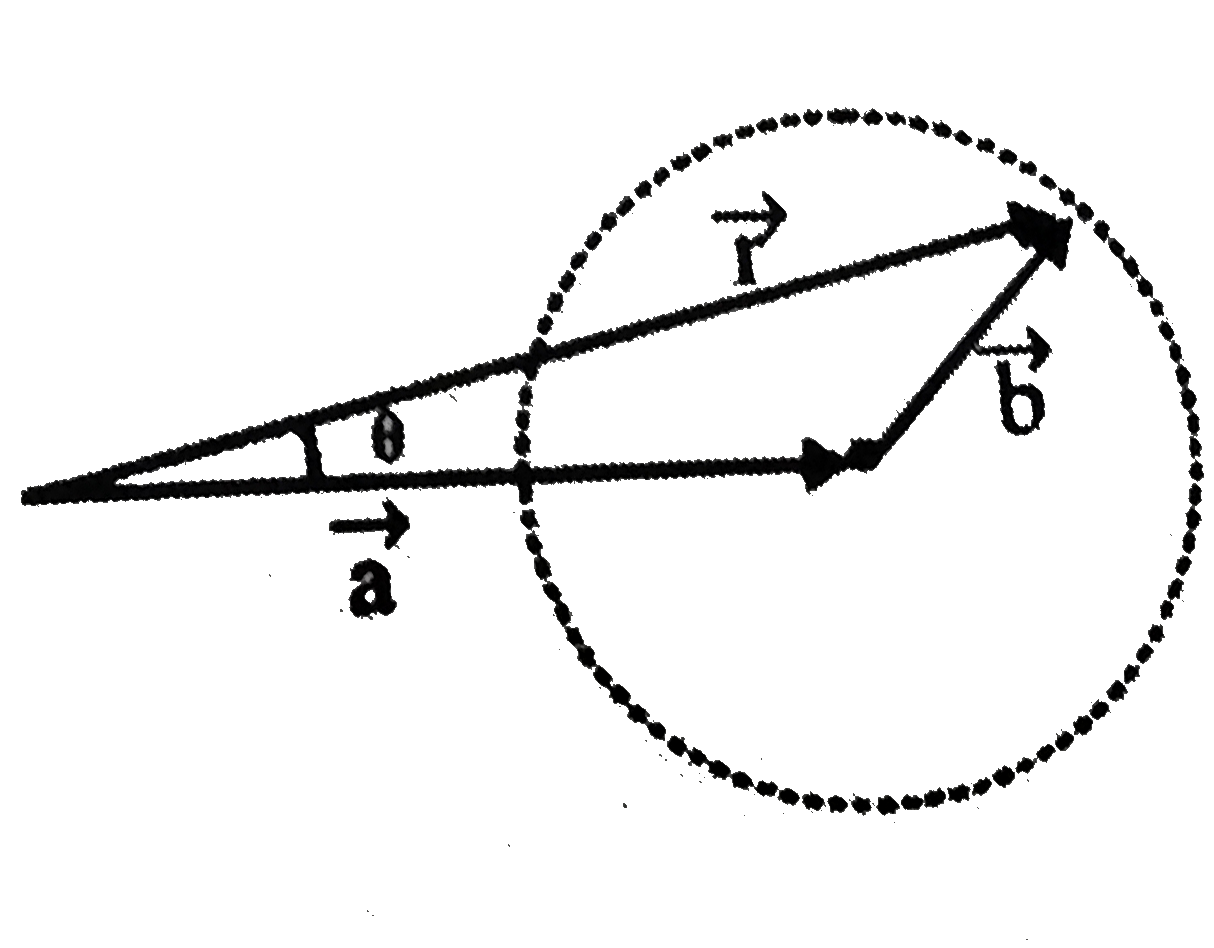
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
View Solution