Find the time constant (∈)fothegivenRC∘uits∈thegivenorderrespectively<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_EIA_C15_019_Q01.pngwh=80%mx-autosty≤=background:white;>,<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_EIA_C15_019_Q02 .pngwh=80%mx-autosty≤=background:white;><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_EIA_C15_019_Q03.pngwh=80%mx-autosty≤=background:white;><br>(R_1)=1 Omega, (R_2)=2 Omega, C_(1)=4 muF, C_(2)=2 mu F
18,4,89
18,89,4
4,18,89
4,8/9,18
The correct Answer is:B
Time constant of R-C circuit is (τ)=(Req)(Ceq)
(i) (τ1)=(2+1)(2+4)=18(μ)s
(ii) (τ2)=(2×12+1)(2×42+4)=89(μs)
(iii)(τ3)=(2×12+1)×(4+2)=4(μs).
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the time constant (in μs) for the given RC circuits in the given order respectively.
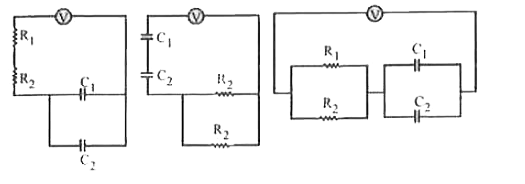
R1=1ω,R2=2ω,C1=4μF,C2=2μFA18,4,89B18,89,4C4,18,89D4,89,18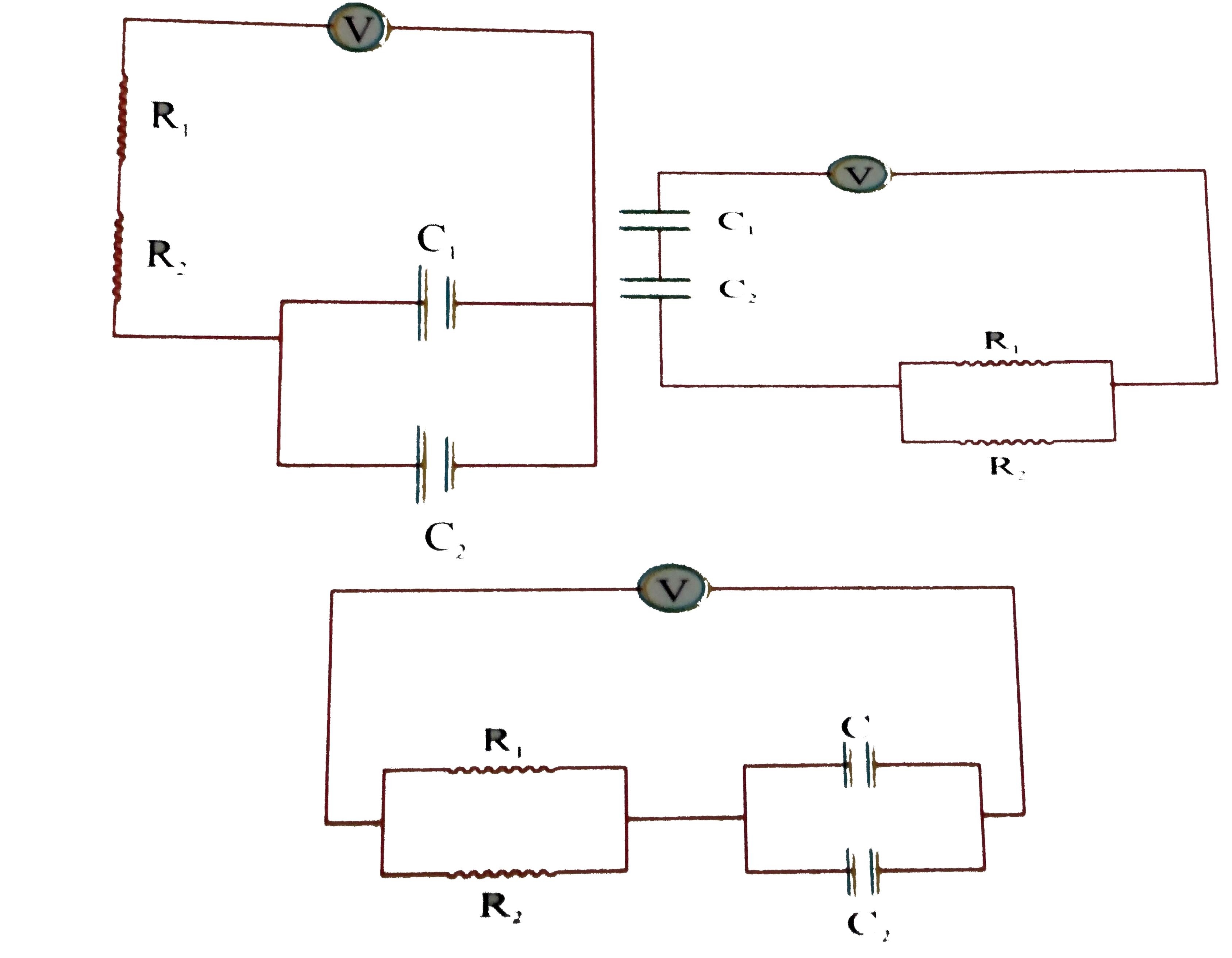
Find the time constant for the given RC circuits in correct order (in μs)
R1=1Ω,R2=2Ω,C1=4μF,C2=2μFA18,4,89B18,89,4C4,18,89D4,89,18Initially the switch 'S' is open for a ling time. Now the switch 'S' is closed at t=0(R1=2Ω,R2=2Ω,C1=1F and C2=1F) Then
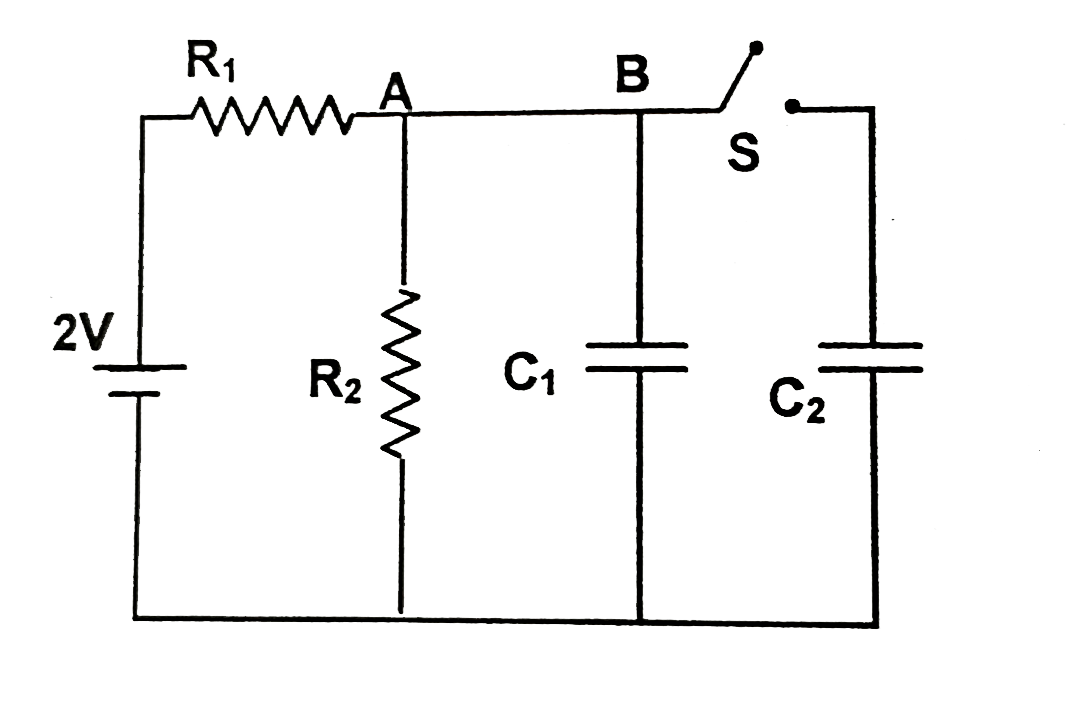 AThe current through the wire AB at t=2 sec is 1/2e ampereBThe current through the wire at t=2 sec is 1/e ampere.CThe charge on the capacitor C2, which has initially unchargd at t=2 sec is (1−12e) coulimbsDThe charge on the capacitor C1 at t=2 sec is (1−12e) coulombs
AThe current through the wire AB at t=2 sec is 1/2e ampereBThe current through the wire at t=2 sec is 1/e ampere.CThe charge on the capacitor C2, which has initially unchargd at t=2 sec is (1−12e) coulimbsDThe charge on the capacitor C1 at t=2 sec is (1−12e) coulombs
In the circuit shown in fig. the switch is kept closed in position 1 for a long time. At time t=0 the switch is moved to position 2. Write the dependence of voltage (VC) across the capacitor as a function of time (t). Take VC to be positive when plate a is positive.
Given: R1=20Ω,R2=60Ω,R3=400kΩ,V1=40V,V2=90VandC=0.5μF.

View SolutionDetermine the voltage drop across the resistor R1 in the circuit given below with E = 65V, R_1 = 50 OmegaR_2 = 100 Omega, R_3 = 100 Omega, and R_4 300 Omega.

View SolutionIn the given circuit, R1 = 10Ω R2=6Omega and E = 10V, then correct statement is
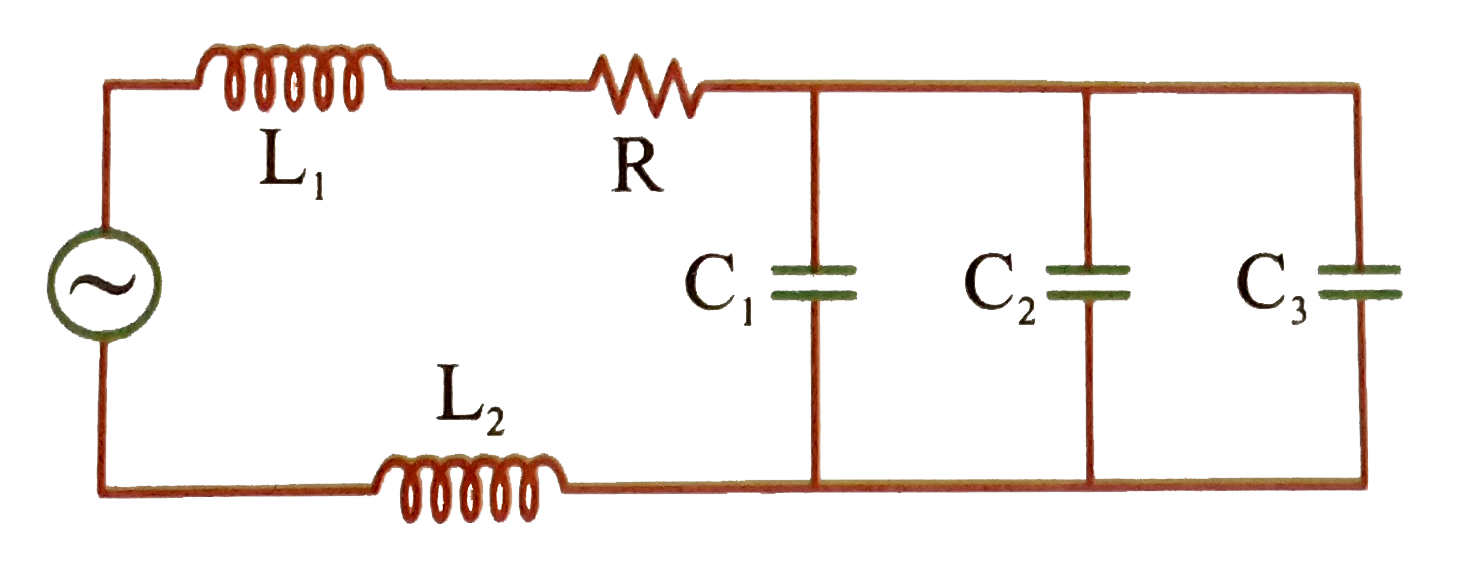
View SolutionA generator with an adjustable frequency of oscillaton is connected to resistance, R=1000Ω, inductance, L1=1.7mH and L2=2.3mH and capacitance, C1=4μF,C2=2.5μF and C3=3.5μF. The resonant angular frequency of the circuit is
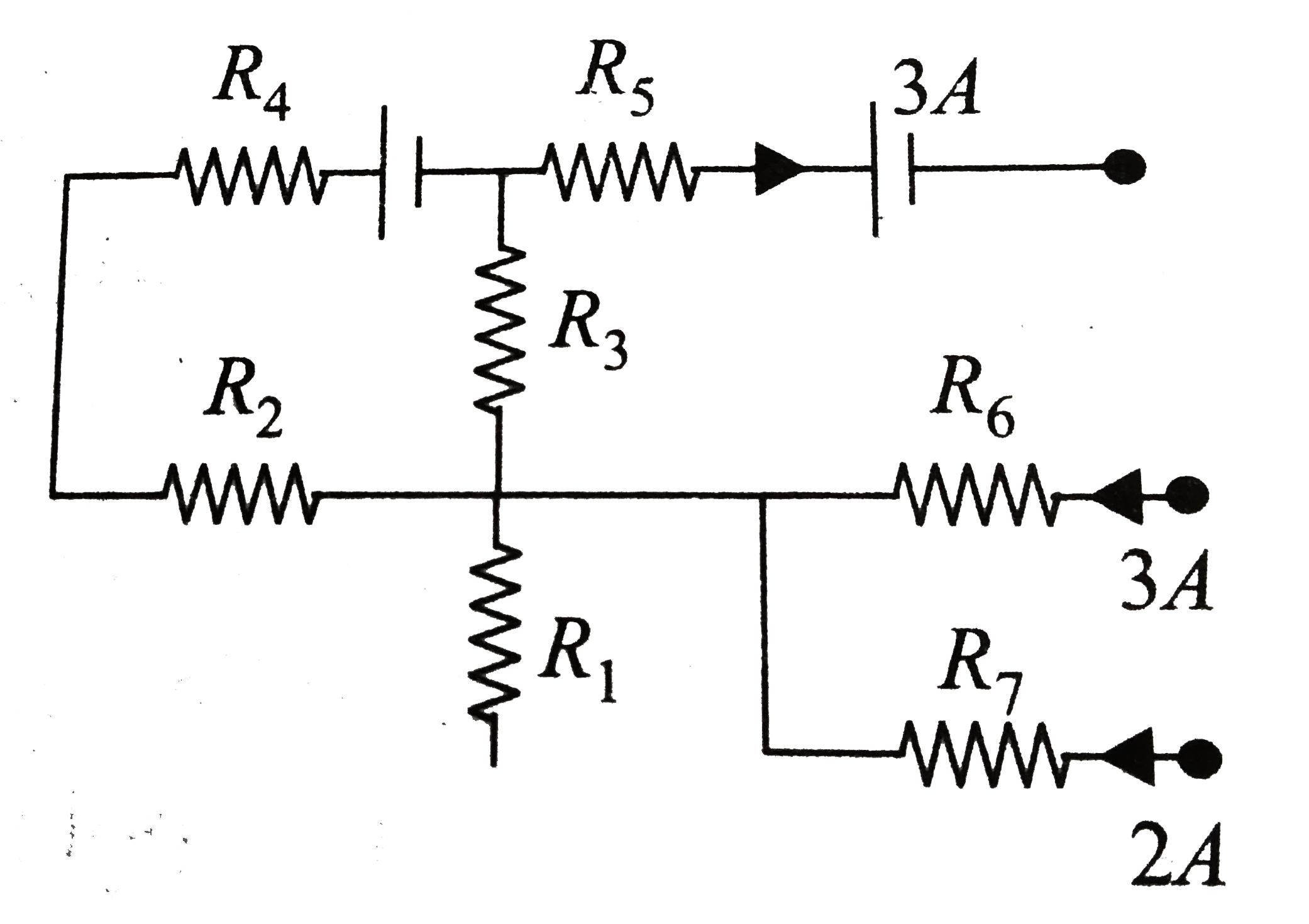
View SolutionIn the given circuit, if I1andI2 be the current in resistances R1andR2, respectively, then
 .
.
View Solution
