Following are four different relation about displacement,velocity and acceleration for the motion of a particle in general.Choose the incorrect one (S).
a) Vav=12[v(t1)+v(t2)]
b)Vav=r(t2)−r(t2)t2−t1
c)r=12(v(t2)−v(t1)(t2−t1)
d)aav=v(t2)−v(t1)t2−t1
a and b
a and d
b and c
a and c
The correct Answer is:D
To determine the incorrect relation among the four given options regarding displacement, velocity, and acceleration, let's analyze each option step by step.
Step 1: Analyze Option (a)
Relation: Vav=12(v(t1)+v(t2))
Explanation: This equation suggests that the average velocity is the arithmetic mean of the velocities at two different times t1 and t2. However, average velocity is defined as the total displacement divided by the total time taken. This relation is only valid if the motion is uniform (constant velocity). Therefore, this relation is incorrect in general.
Step 2: Analyze Option (b)
Relation: Vav=r(t2)−r(t1)t2−t1
Explanation: This equation correctly defines the average velocity as the change in displacement divided by the change in time. This is a standard definition in physics and is correct.
Step 3: Analyze Option (c)
Relation: r=12(v(t2)−v(t1))(t2−t1)
Explanation: This equation suggests that displacement r is equal to half the product of the change in velocity and the time interval. However, displacement is actually calculated using average velocity, not instantaneous velocities. The correct relation should involve average velocity, not just the difference in velocities. Thus, this relation is also incorrect.
Step 4: Analyze Option (d)
Relation: aav=v(t2)−v(t1)t2−t1
Explanation: This equation correctly defines the average acceleration as the change in velocity divided by the change in time. This is a standard definition in physics and is correct.
Conclusion
The incorrect relations are:
- (a) Vav=12(v(t1)+v(t2))
- (c) r=12(v(t2)−v(t1))(t2−t1)
Summary of Incorrect Options
- Incorrect Options: (a) and (c)
Relation: Vav=12(v(t1)+v(t2))
Relation: Vav=r(t2)−r(t1)t2−t1
Relation: r=12(v(t2)−v(t1))(t2−t1)
Relation: aav=v(t2)−v(t1)t2−t1
The incorrect relations are:
- (a) Vav=12(v(t1)+v(t2))
- (c) r=12(v(t2)−v(t1))(t2−t1)
- Incorrect Options: (a) and (c)
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -II
80 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE
58 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
A particle executes simple harmonic motion about x=0 along x-axis. The position of the particle at an instant is given by x=(5cm)sinπt. Find the average velocity and average acceleration for a time interval 0−0.5s.
Hint : Average velocity =x2−x1t2−t1
x1=5sin0
x2=5sin(π×0.5)
t2−t1=0.5
Average acceleration =v2−v1t2−t1
v=dxdt=5πcosπt
⇒aav=5πcos(π×0.5)−5πcosθ0.5
View SolutionWhich among the following relations is correct?
(a)t3/4=2t1/2
(b)t3/4=3t1/2
(c)t3/4=12t1/2
(d)t3/4=13t1/2
View Solution
Knowledge Check
For any arbitrary motion in space, which of the following relations are true?
a) vaverage=(1/2)(v(t1+v(t2)
b) vaverage=[r(t2)−rt1t2−t1
v(t)=v(0)+at
d) aaverage=[v(t2)−vt1t2−t1
The average stands for average of the quantity over time interval t1 to t_(2)A→vaverage=12[→v(t1)+→v(t2)]B→vaverage=→r(t2)−→r(t1)t2−t1C→v(t)=→v(0)+→atD→r(t)=→r(0)+→v(0)t+12→at2Two different adiabatic parts for the same gas intersect two isothermals at T1andT_2 as shown in P-V diagram . Then the ratio of VaVb will be
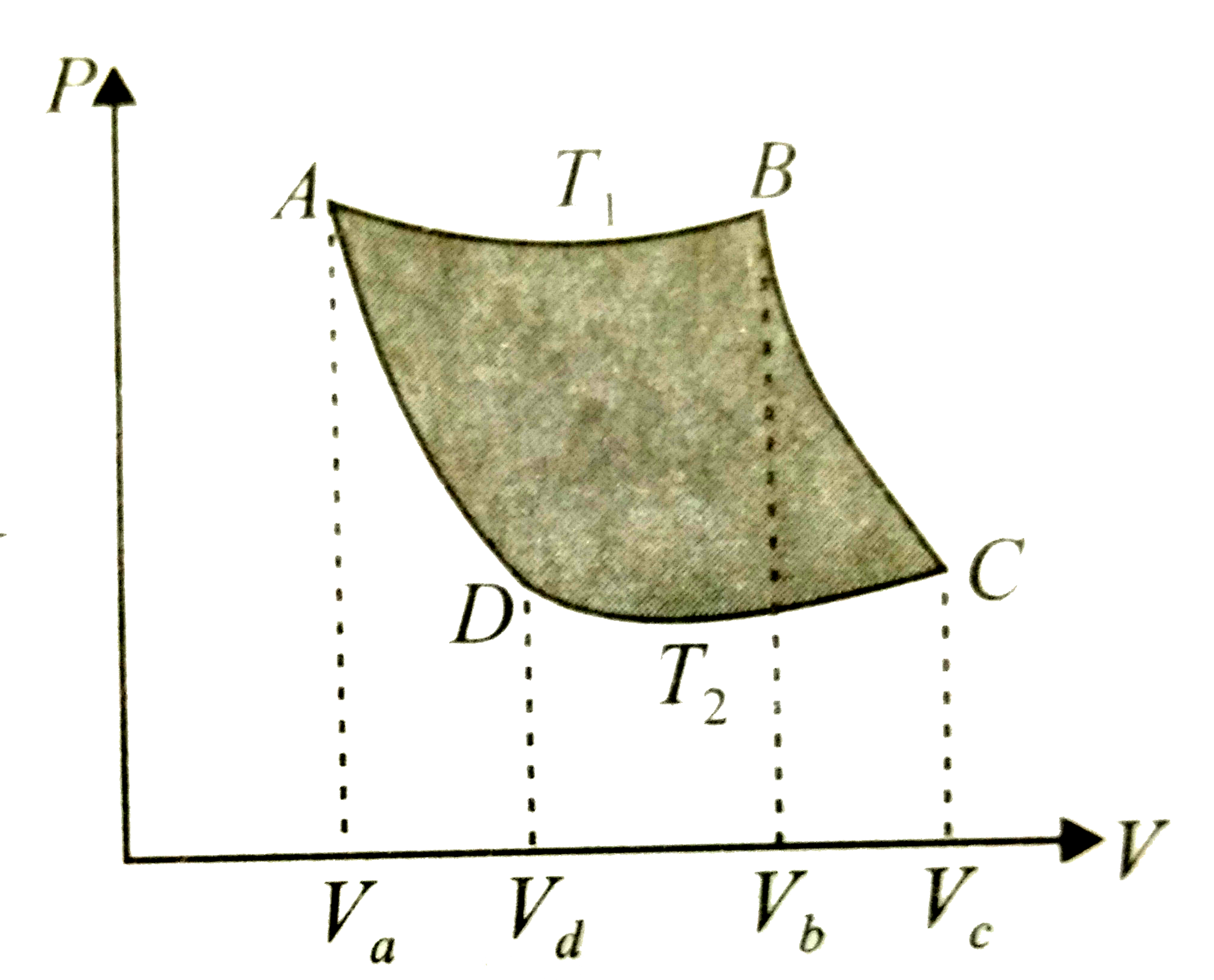 Aa. VcVdBb. VdVcCc. γVdVcDd. 1γVdVc
Aa. VcVdBb. VdVcCc. γVdVcDd. 1γVdVc
Velocity of a particle at any time t is v=(2ˆi+2tˆj)m/s. Find acceleration and displacement of particle at t=1s. Can we apply v=u+at or not?
View SolutionThe correct relation between tav=average life and t1/2= half life for a radioactive nuclei.
View SolutionExamine the following plots and predict whether in (i) P1<P2andT1>T2 , in (ii) T1=T2<T3, in (iii) V1>V2,in(iv)P1>P2orP2>P1
_E01_267_Q01.png)
View SolutionThe x-t equation is given as x=2t+1. The corresponding v-t graph is
View SolutionIf the normal at t1 on the parabola y2=4ax meet it again at t2 on the curve then t1(t1+t2)+2 = ?
View SolutionVelocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
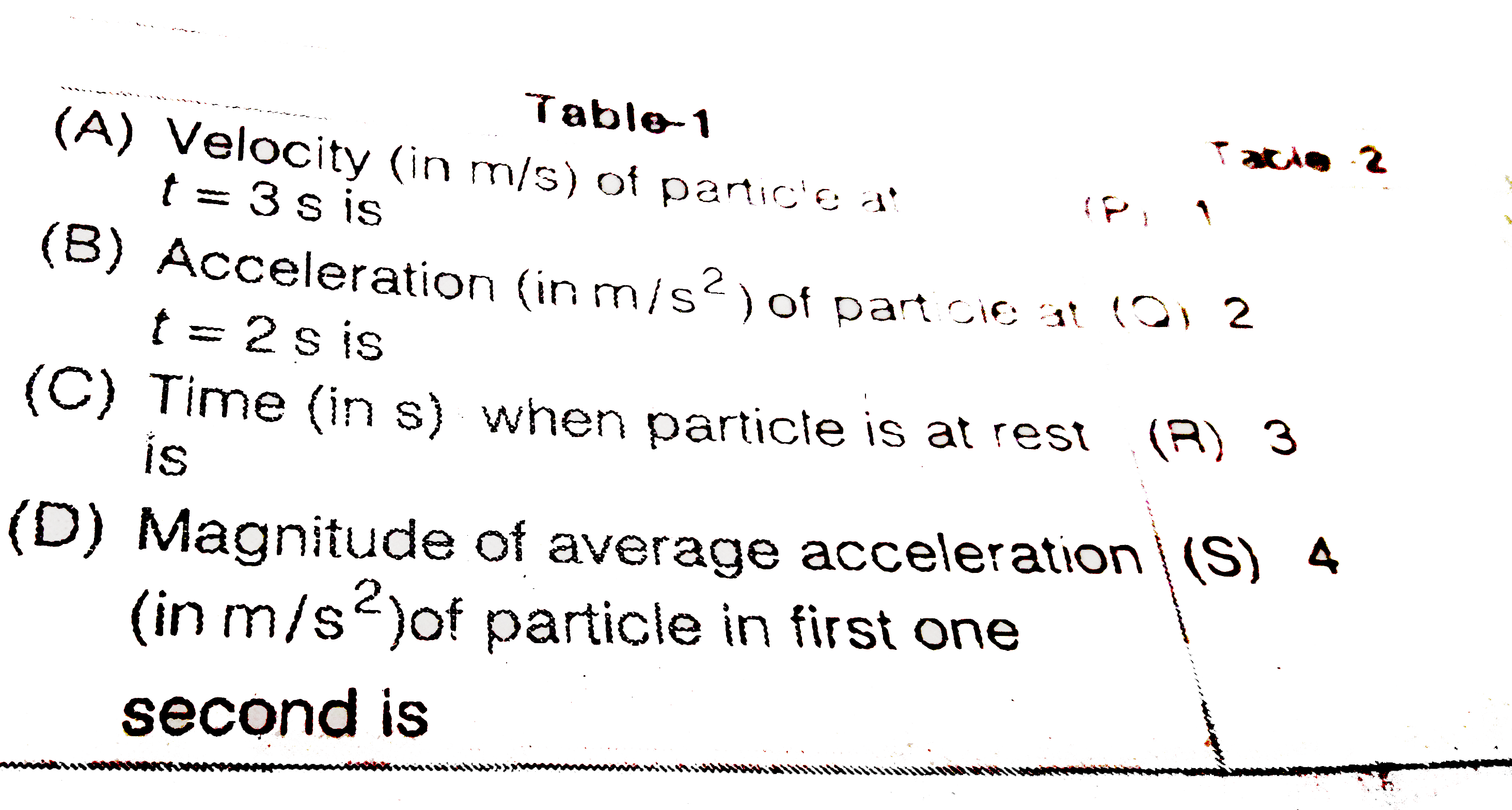
View Solution
