Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
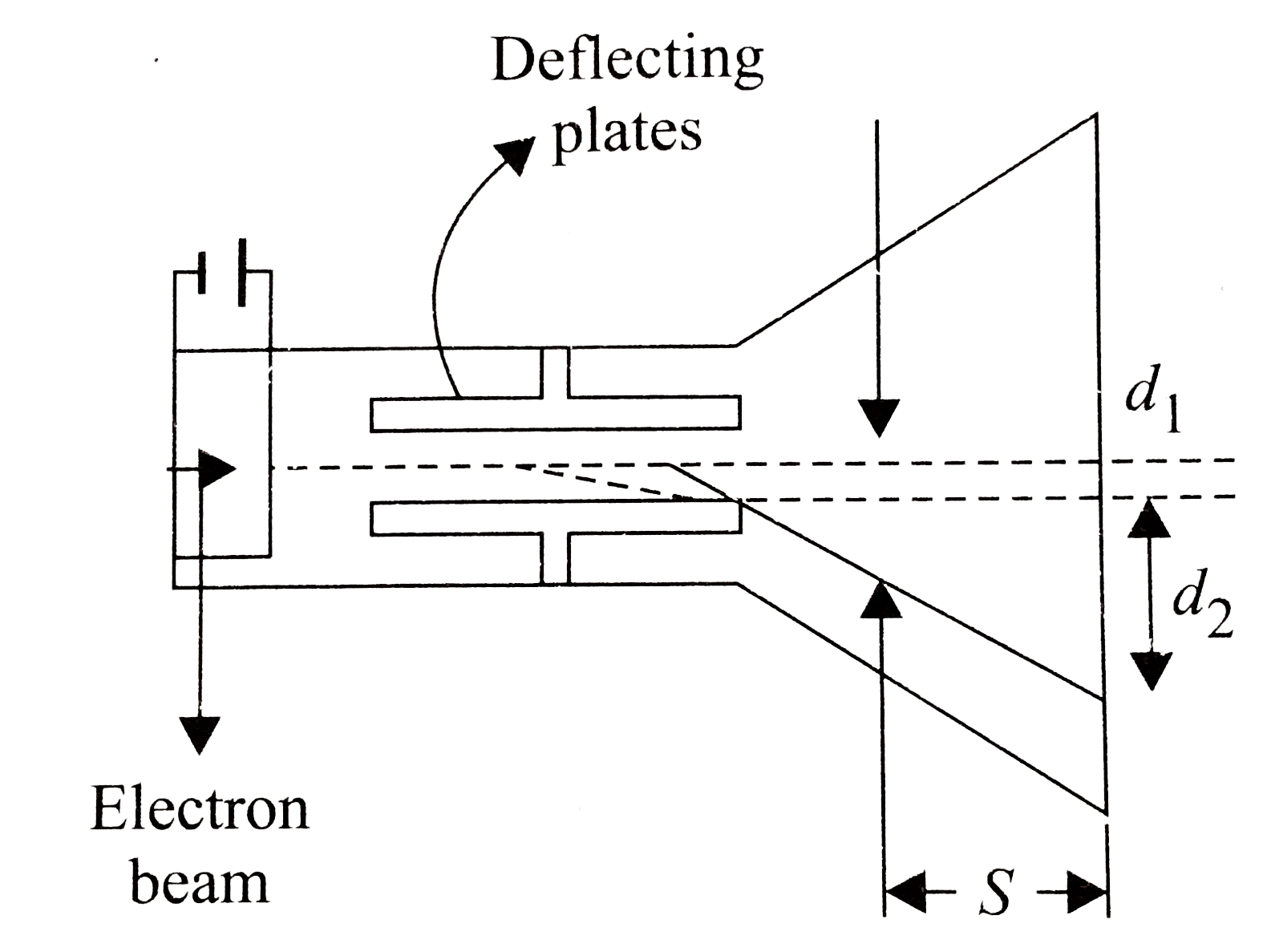
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron is
1.5×1011Ckg−1
2×1011Ckg−1
2.5×1011Ckg−1
3×1011Ckg−1
The correct Answer is:B
Since d1=eEL22mv2orem=2d1v2EL2
Here d1=2×10−3m
v=3×107m/sL=0.1m
E=1800V/m
em=2×(2×10−3)×(3×107)21800×(0.1)2=2×1011C/kg.
Hence choice (b) is correct.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
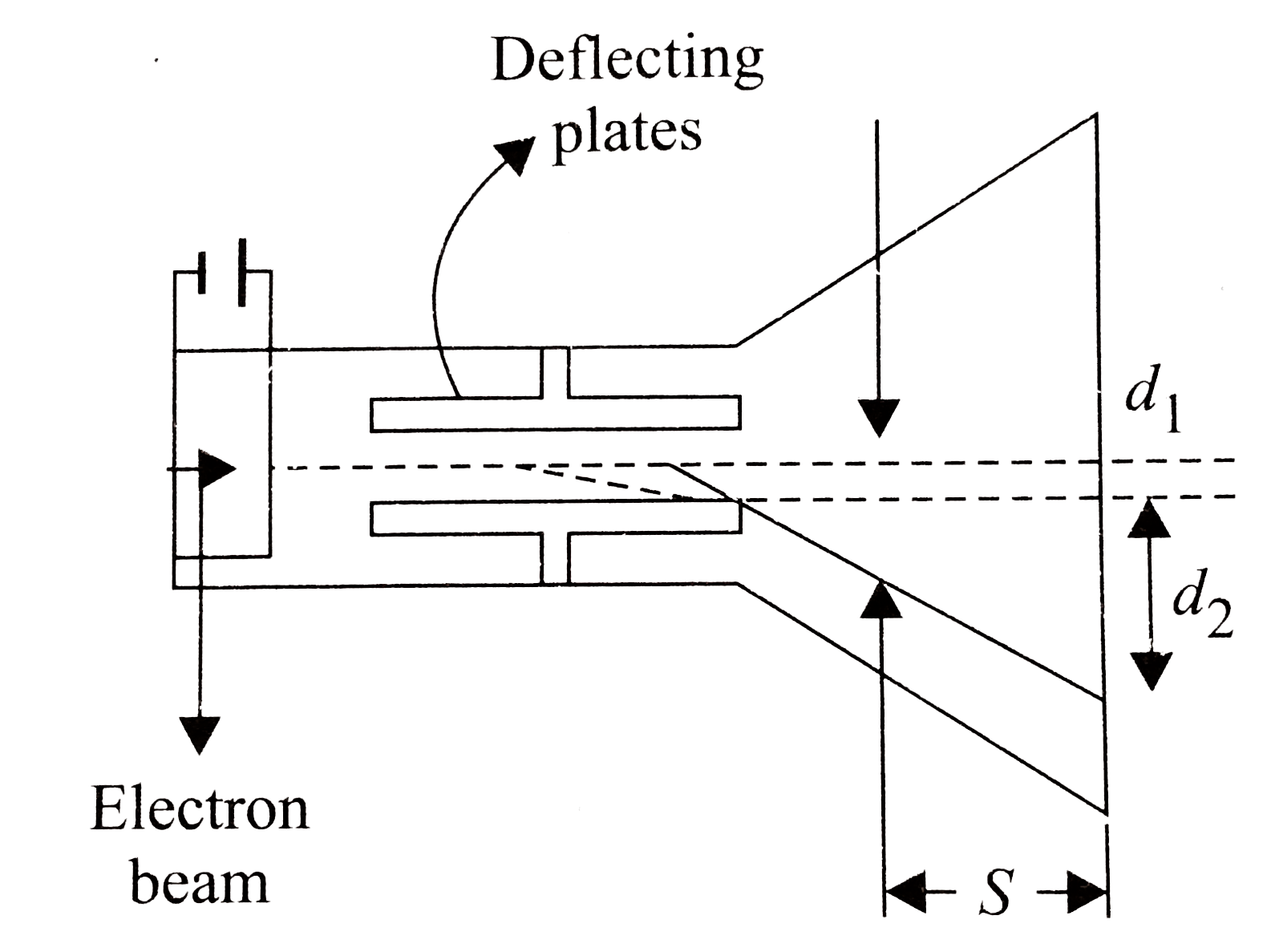
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experimentView SolutionAn electron experiment was performed with a beam of electron accelerated by a potential difference of 10.0keV .What is the wavelength of the electron beam
View Solution
Knowledge Check
- Question 1 - Select One
The ratio of charge to mass of an electron in coulombs per gram was determined by J.J. Thomson. He determined this ratio by measuring the deflection of cathode rays in electric and magnetic fields. What value did he find for this ratio?
A−1.76×108 coulombs/gB1.76×10−8 coulombs/gC−1.76×1010 coulombs/gD−1.76×10−10 coulombs/g
If an electron is not deflected in passing through a certain region of space can we be sure that there is no magnetic field in that region?
View SolutionThe mass of an electron is m, charge is e and it is accelerated form rest through a potential difference of V volts. The velocity acquired by electron will be :
View SolutionElectrons are emitted by a hot filament and are accelerated by an electric field as shown in figure .The two stops at the left ensure that the electron beam has a uniform cross-section.
 View Solution
View SolutionAn electron in the beam of a TV picture tube is accelerated by a potential difference of 2.00kV. Then, it passes through region of transverse magnetic field, where it moves in a circular arc with radius 0.180m. at is the magnitude of the field?
View SolutionA beam of electrons passes undeflected through uniformly perpendicular electric and magnetic fields. If the electric field is switched off, and the same magnetic field is maintained then the electrons move:
View SolutionIn an electron gun, the electrons are accelerated by the potential V. If the e is the charge and m is the mass of the electron, then the maximum velocity of these electrons will be
View SolutionThe mass of an electron is m, its charge is e and it is accelerated from rest through a potential difference, V. The velocity of electron can be calculated by formula:
View Solution
