For an equilateral prism, it is observed that when a ray strikes grazingly at one face, it emerges grazingly at the other face, its refractive index will be
2
The correct Answer is:C
To find the refractive index (μ) of an equilateral prism when a ray strikes grazingly at one face and emerges grazingly at the other face, we can follow these steps:
1. Understand the Geometry of the Prism:
- An equilateral prism has angles of 60 degrees each. Let's denote the angle of the prism as A=60∘.
2. Incident and Emergent Ray:
- When a ray strikes grazingly at one face, it means that the angle of incidence i is such that it is just about to enter the prism. Similarly, it emerges grazingly at the other face, meaning the angle of emergence e is also at the critical angle.
3. Apply Snell's Law:
- For the first face, applying Snell's law:
μsin(i)=1⋅sin(r1)
- For the second face, since the ray emerges grazingly:
1⋅sin(r2)=μsin(e)
4. Relate Angles:
- Since the ray is incident and emerging grazingly, we have i=e. Thus, we can denote r1=r and r2=r.
- From the property of the prism, we know that:
r1+r2=A⟹r+r=60∘⟹2r=60∘⟹r=30∘
5. Substituting Values:
- Now substituting r back into Snell's law:
μsin(30∘)=1⋅sin(30∘)
- Since sin(30∘)=12:
μ⋅12=1⋅12
6. Solve for Refractive Index:
- Rearranging gives:
μ=1sin(30∘)=112=2
Final Answer:
The refractive index μ of the equilateral prism is 2.
---
- An equilateral prism has angles of 60 degrees each. Let's denote the angle of the prism as A=60∘.
- When a ray strikes grazingly at one face, it means that the angle of incidence i is such that it is just about to enter the prism. Similarly, it emerges grazingly at the other face, meaning the angle of emergence e is also at the critical angle.
- For the first face, applying Snell's law:
μsin(i)=1⋅sin(r1)
- For the second face, since the ray emerges grazingly:
1⋅sin(r2)=μsin(e)
- Since the ray is incident and emerging grazingly, we have i=e. Thus, we can denote r1=r and r2=r.
- From the property of the prism, we know that:
r1+r2=A⟹r+r=60∘⟹2r=60∘⟹r=30∘
- Now substituting r back into Snell's law:
μsin(30∘)=1⋅sin(30∘)
- Since sin(30∘)=12:
μ⋅12=1⋅12
- Rearranging gives:
μ=1sin(30∘)=112=2
The refractive index μ of the equilateral prism is 2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)73videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct20videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
Similar Questions
For an equilateral prism, it is observed that when a ray strikes grazingly at one face it emerges grazingly at the other. Its refractive index will be
View SolutionA narrow beam of monochromatic light, PQ, is incident normally on one face of an equiangular glass prism of refractive index 1.45. When the prism is immersed in a certain liquid, the ray makes a grazing emergence along the other face (figure). Find the refractive index of this liquid .
View SolutionA narrow beam of monochromatic light, pe, is incident normally on one face of an equiangular glass prism of refractive inder 1-45. When the prism is immersed in a certain liquid, the ray makes a grazing emergence along the other face (See below figure). Find the refractive index of this liquid.
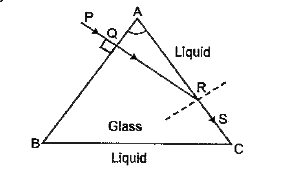 View Solution
View SolutionA ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges and calculate the refractive index of the material of prism.
View SolutionA ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges and calculate the refractive index of the material of prism.
View SolutionThere is a equilateral prism of refractive index 3 on which a light ray is incident normally on one face as shown in the figure. Find the length of the path traveled by the light ray inside the prism.
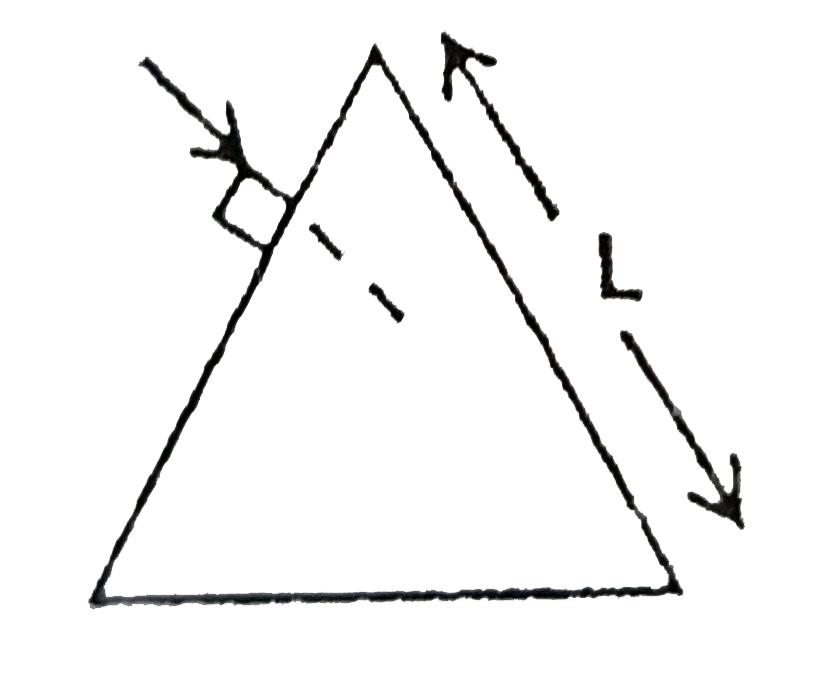 View Solution
View SolutionA ray of light is normally incident on one face of an equilateral glass prism. Answer the following :
(a) What is the angle of incidence on the first face of the prism?
(b) What is the angle of refraction from the first face of the prism ?
(c) What will be the angle of incidence at the second face of the prism ?
(d) Will the light ray suffer minimum deviation by the prism ?View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60∘ so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
View SolutionA ray of light is incident on the face AB of a glass prism ABC having vertex anlge A equal to 30∘. The face AC is silvered and a ray of light incident on the face AB retraces its path. If the refractive index of the material of prism is √3 find the angle of incidence on the face AB.
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
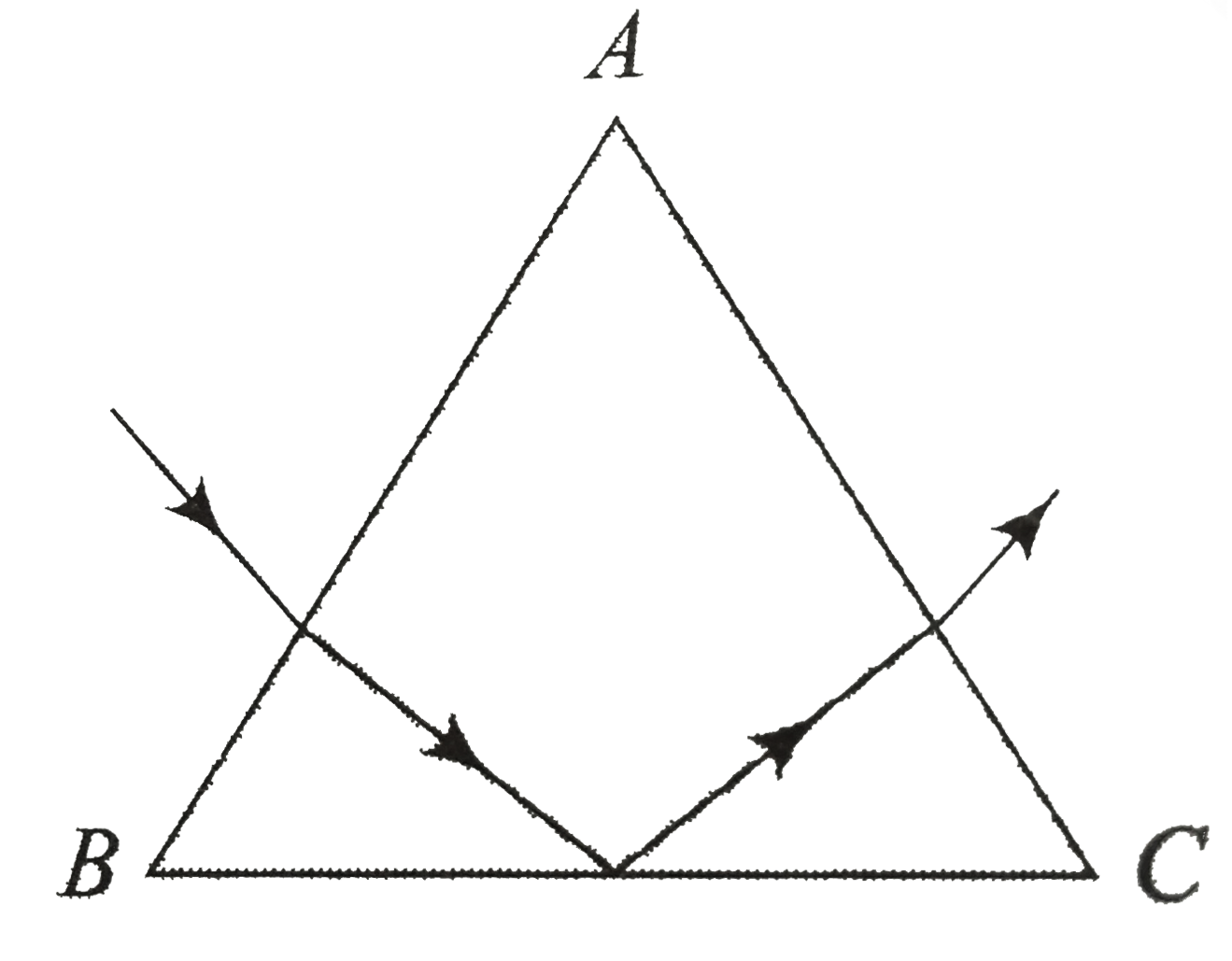 View Solution
View Solution

