For the potential energy curve shown in figure.
(a) Determine whether the force Fx is positive, negative, or zero at the five points indicated, (b) Indicate points of stable, unstable, and neutral equilibrium, (c) Sketch the curve for Fx versus x from x=0 to x=8m.
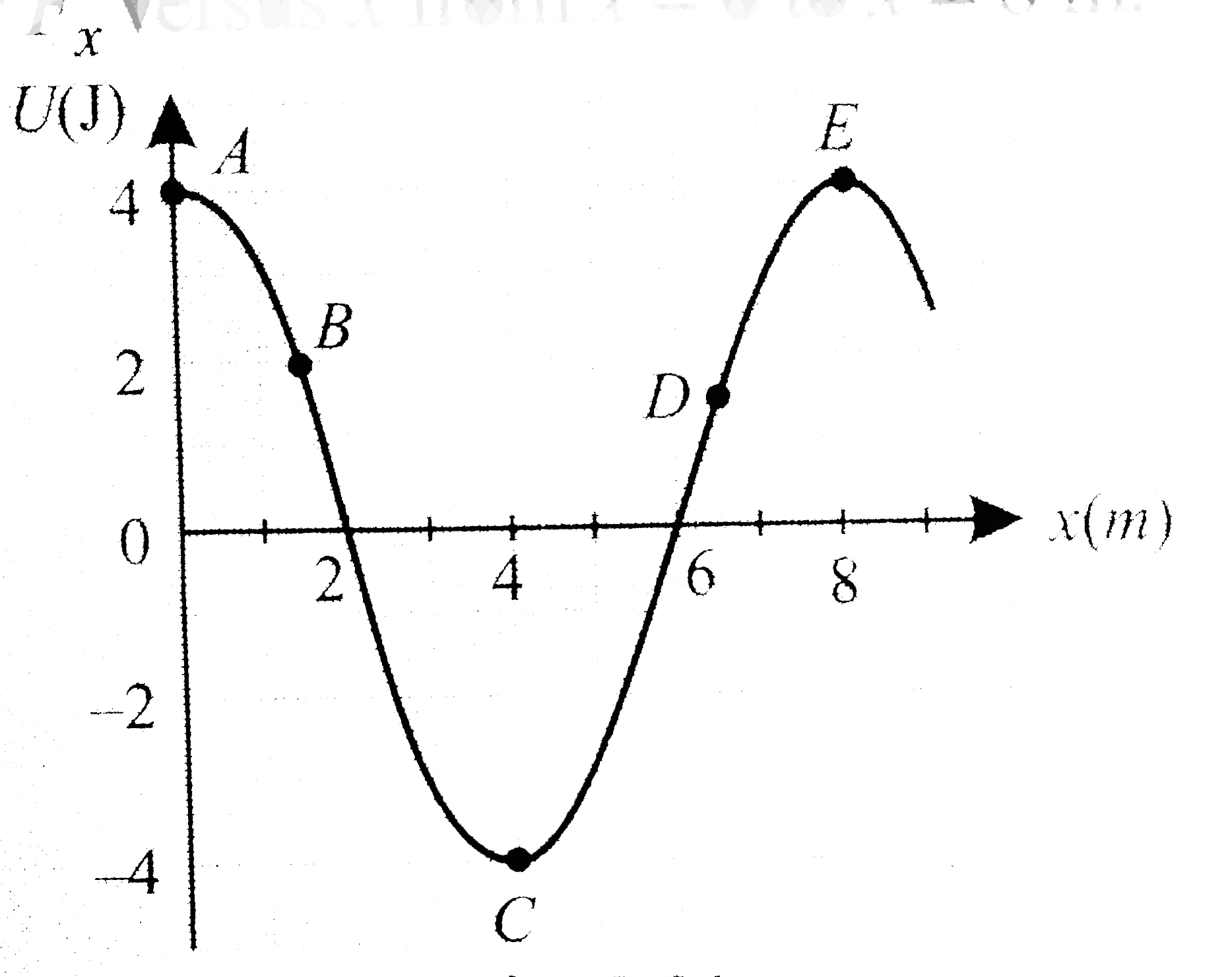
a. Fx is zero at points A, C, and E, Fx is positive at point B and negative at point D
b. A and E are unstable, and C is stable.
c. 
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.4
16 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
For the potential energy curve shown shown in figure.
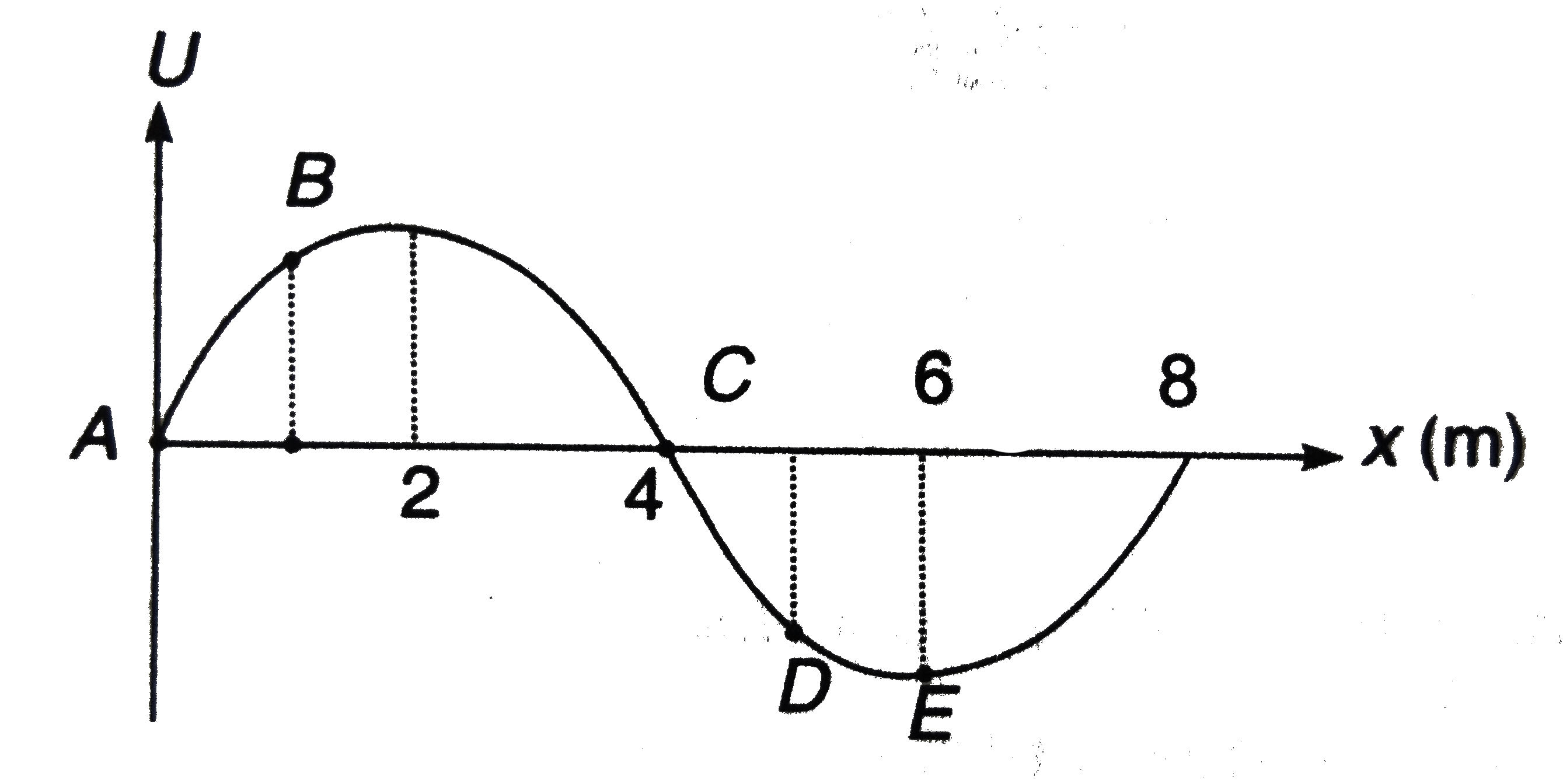
(a) Find directions of force at points A,B,C,D and E.
(b) Find positions of stable, unstable and neutral equilibriums.
View SolutionForce acting on a particle moving along x-axis as shown in figure. Find points of stable and unstable equlibrium.
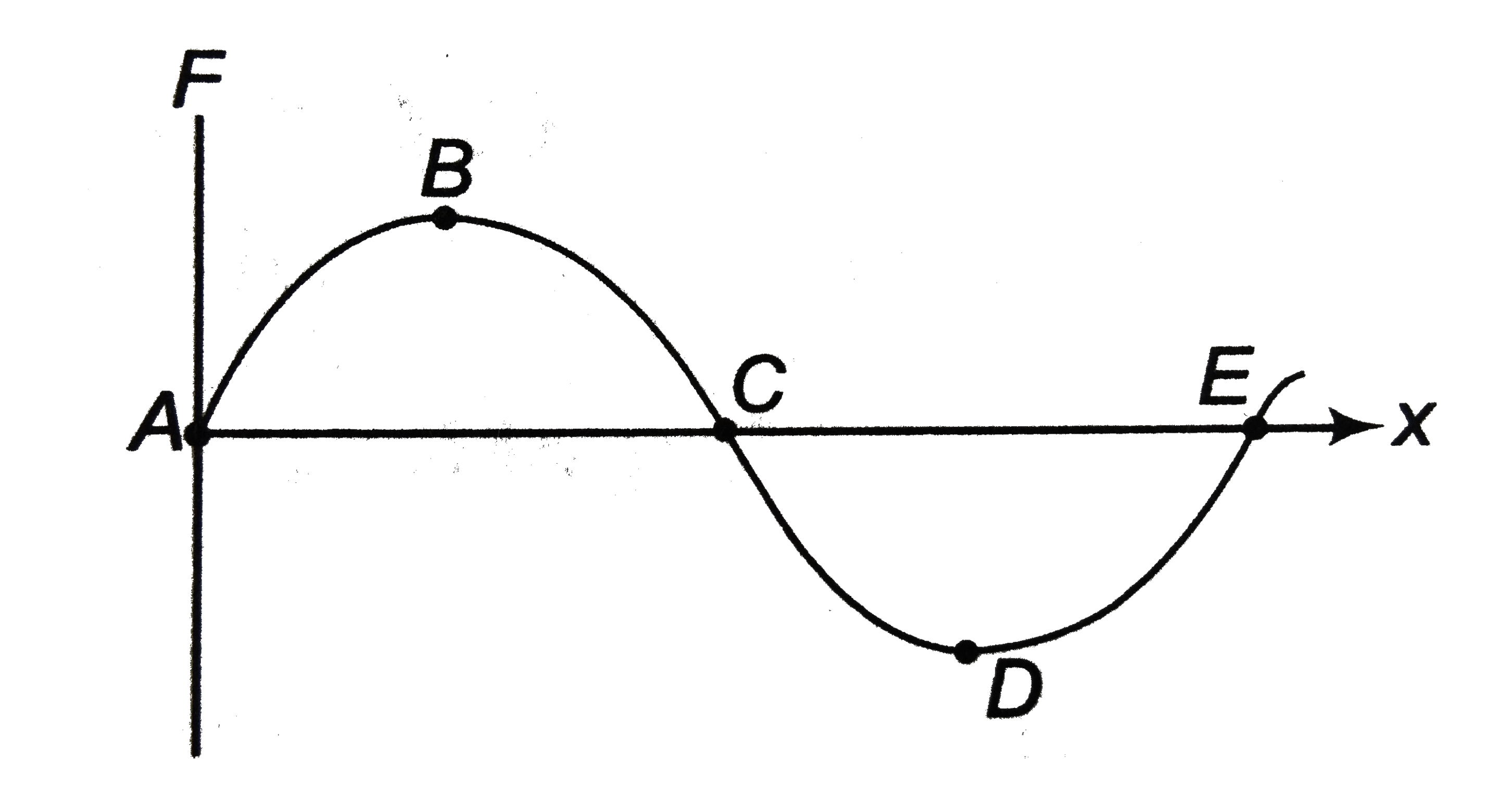 .
.
View SolutionDetermine the quadratic curve y=f(x) if it touches the line y=x at the point x=1 and passes through the point (−1,0).
View SolutionThe potential energy of a conservative force field is given by
U=ax2−bx
where, a and b are positive constants. Find the equilibrium position and discuss whether the equilibrium is stable, unstable or neutral.
View SolutionDetermine the quadratic curve y=f(x) if it touches the line y=x at the point x=1 and passes through the point (−1, 0) .
View SolutionFind the equations of the tangent and the normal to the curve y=x2 at (0, 0) at the indicated points
View SolutionA particle of mass m=1kg lying on x-axis experiences a force given by law
F=x(3x−2) Newton.
Where x is the x-coordinate of the particle in meters.
−−−−−−−−−→x=0x=4
(a) Locate the point on x-axis where the particle is in equilibrium.
(b) Draw the graph of variation of force F (y-axis) with x-coordinate of the particle (x-axis). Hence or otherwise indicate at which positions the particle is in stable or unstable equilibrium.
(c ) What is the minimum speed to be imparted to the particle placed at x=4 meters such that it reaches tha origin.
View SolutionFind the equations of the tangent and the normal to the curve y=x2+4x+1 at x=3 at the indicated points
View SolutionFind the equations of the tangent and the normal to the curve xy=c2 at (ct, c/t) at the indicated points.
View SolutionFind the equations of the tangent and the normal to the curve y=2x2−3x−1 at (1, −2) at the indicated points
View Solution
