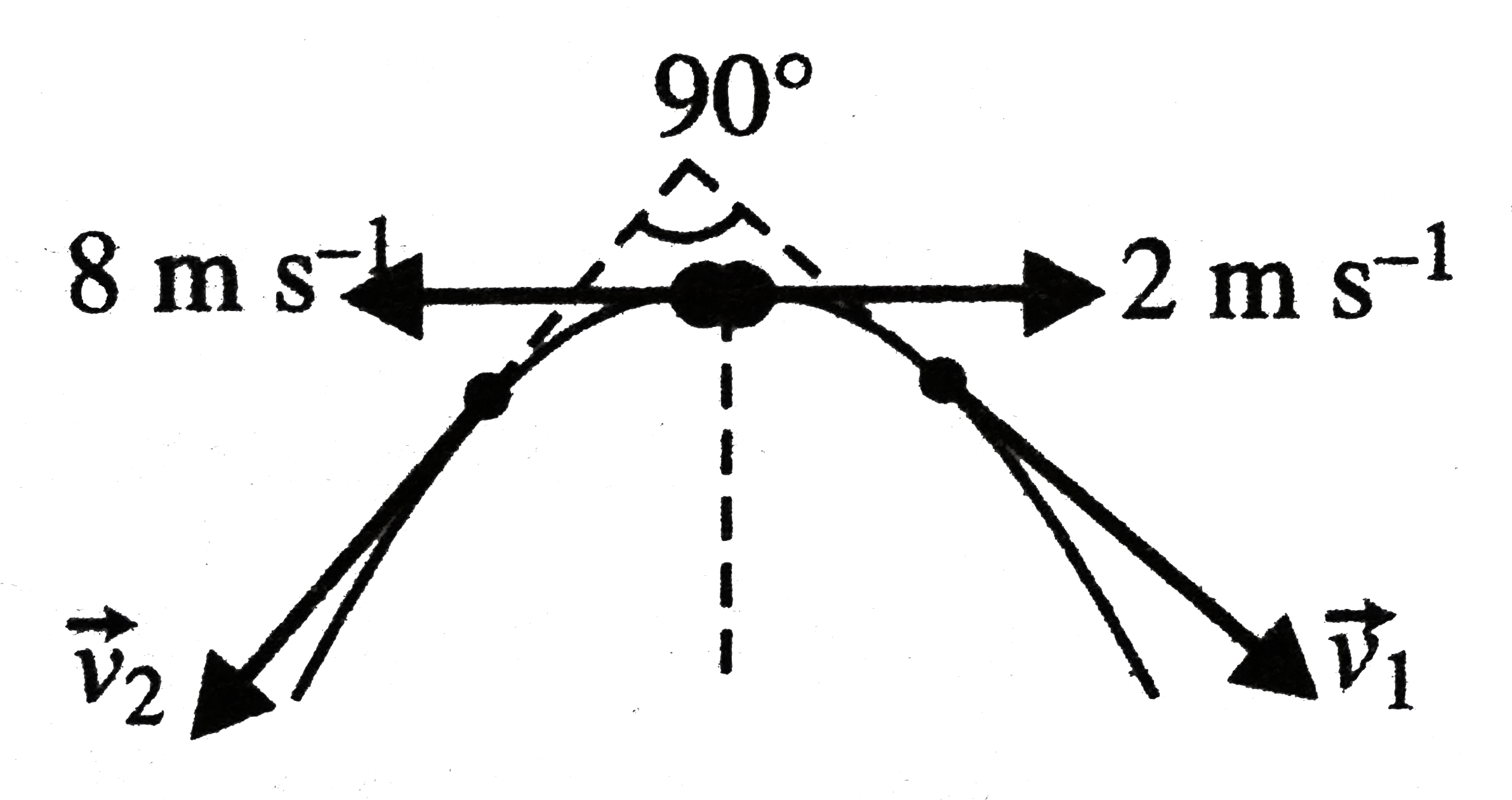
From a tower of height $40 m$ , two bodies are simultaneously projected horizontally in opposite direction, with velocities $2 m s^{- 1} and 8 m s^{- 1}$ . respectively.
The time taken for the displacement vectors of two bodies to be come perpendicular to each other is.

A

0.1 s

B

0.2 s

C

0.8 s

D

0.6 s

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

(d) Velocity of first body at any instant t, ${\to v}_{1} = 2 ˆ i - gt ˆ j$
Velocity of second body at any instant
${\to v}_{2} = - 8 ˆ i - gt ˆ j$
Since ${\to v}_{1} ⊥ {\to v}_{2}, i . e ., {\to v}_{1} . {\to v}_{2} = 0$
$(2 ˆ i - gt ˆ j) . (- 8 ˆ i - gt ˆ j) = 0 \Rightarrow - 16 + g^{2} t^{2} = 0$
$\Rightarrow t = \sqrt{\frac{16}{g^{2}}} \Rightarrow t = \frac{4}{10} = 0.4 s$
${\to S}_{1} = (2 \times 0.4) ˆ i, {\to S}_{2} = (8 \times 0.4) (- ˆ i)$
${\to S}_{1} = 0.8 ˆ i and {\to S}_{2} = - 3.2 ˆ i$
Separation $= {\to S}_{1} - (- {\to S}_{2}) = 0.8 ˆ i + (3.2 ˆ i) = 4 ˆ i$
${\to S}_{1} = 2 t ˆ i - \frac{1}{2} {gt}^{2} ˆ j, {\to S}_{2} = - 8 t ˆ i - \frac{1}{2} {gt}^{2} ˆ j$
As ${\to S}_{1} ⊥ {\to S}_{2}, i . e ., {\to S}_{1} . {\to S}_{2} = 0$
$- 16 t + \frac{1}{2} \times \frac{1}{2} g^{2} t^{2} = 0 \Rightarrow g^{2} t^{2} = 16 \times 4$
$\Rightarrow > = 4 \times 2 \Rightarrow t = \frac{8}{10} = 0.8 s$ .
.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two trains, each 50 m long are travelling in opposite direction with velocity 10 m/s and 15 m/s. The time of crossing is
A2s
B4s
C $2 \sqrt{3} s$
D $4 \sqrt{3}$ s
Question 2 - Select One
Two trains 121 m and 99 m in length are running in opposite directions with velocities $40 k m h^{- 1}$ and $32 k m h^{- 1}$ . In what time they will completely cross each other?
Aa. 9 s
Bb. 11 s
Cc. 13 s
Dd. 15 s

CENGAGE PHYSICS ENGLISH-KINEMATICS-2-Exercise Comprehension

Home
Ask Doubt
Profile