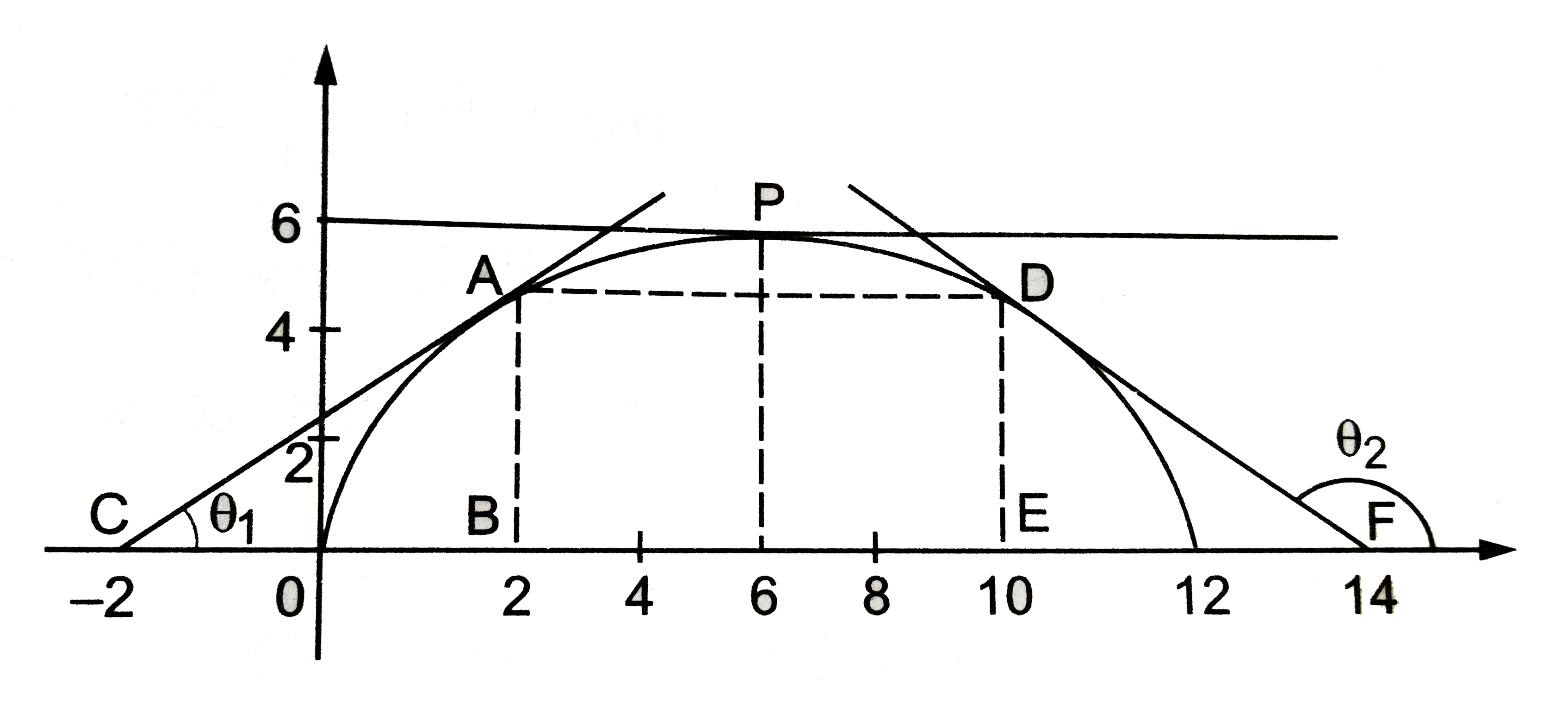
From the curve given in figure find dydxatx=2, 6 and 10.
From the curve given in figure find dy/dx at x=2, 6 and 10.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The tangent to the curve at x=2 is AC. Its slope is tanθ1=ABBC=54
Thus, dydx=54atx=2.
The tangent to the curve at x=6 is parallel to the X-axis.
Thus, dydx=tanθ=0atx=t
The tangent to the curve at x=10 is DF. Its slope is
tanθ2=DEEF=−54 ltbr> Thus, dydx=−54atx=10
If we are given the graph of y versus x, we can find dydx at any pintof the curve bydrawing the tangent at that point and finding its slope. Evwen if the graph is not drawn and the algebraic relation bettween y and x is given in the formof an equation, we can find dydx algebraically. Let us take an example.
The area A of a square of length L is A=L2. ltbr> If we change L to L+△L, the area will change from A to A+△Aure.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C02_S01_006_S06.pngwh=80%mx-autosty≤=background:white;><br>A+/_\A=(L+/_\L)^2<br> = L^2+2L /_\L+(/_\L)^2<br>or,/_\A=2L(/_\L)+/_\L)^2<br>or,(/_\A)/ (/_\L)=2L+/_\L<br>Nowif/_\Lismadesmal≤randsmal≤r,2L+/_\Lwillappraoch2L.<br>Thus,(dA)/dL) = lim_(/_\Lrarr0)=(/_\A)/(/_\L)=2L.

Updated on:21/07/2023
|