Given that T2=kR3, express the constant k of the above relation in days and kilometres. Given, k=10−13s2m−3. The Moon is at a distance of 3.84×105km from the earth. Obtain its time period of revolution in days.
To solve the problem step by step, we will follow these instructions:
Step 1: Convert the constant k from s2m−3 to day2km−3
Given:
k=10−13s2m−3
We need to convert seconds to days and meters to kilometers.
1. Convert seconds to days:
1day=24hours×60minutes×60seconds=86400seconds
Therefore,
1second=186400days
Thus,
1s2=(186400)2day2=1864002day2
2. Convert meters to kilometers:
1m=11000km
Therefore,
1m−3=(1000)3km−3=109km−3
Now, substituting these conversions into k:
k=10−13s2m−3=10−13⋅1864002day2⋅109km−3
Calculating 864002:
864002=7.46496×109
Now substituting this back into the equation:
k=10−13⋅17.46496×109day2⋅109km−3
=10−137.46496day2km−3
≈1.34×10−14day2km−3
Step 2: Use the relation T2=kR3 to find the time period T
Given:
- R=3.84×105km
Substituting the values into the equation:
T2=kR3=(1.34×10−14day2km−3)⋅(3.84×105km)3
Calculating R3:
R3=(3.84×105)3=5.67×1016km3
Now substituting R3 back into the equation:
T2=1.34×10−14⋅5.67×1016
T2≈7.61×102day2
Taking the square root to find T:
T≈√7.61×102≈27.57days
Final Answer:
The time period of the Moon's revolution around the Earth is approximately 27.57days.
---
k=10−13s2m−3
1day=24hours×60minutes×60seconds=86400seconds
Therefore,
1second=186400days
1s2=(186400)2day2=1864002day2
1m=11000km
Therefore,
1m−3=(1000)3km−3=109km−3
k=10−13s2m−3=10−13⋅1864002day2⋅109km−3
864002=7.46496×109
k=10−13⋅17.46496×109day2⋅109km−3
=10−137.46496day2km−3
≈1.34×10−14day2km−3
- R=3.84×105km
T2=kR3=(1.34×10−14day2km−3)⋅(3.84×105km)3
R3=(3.84×105)3=5.67×1016km3
T2=1.34×10−14⋅5.67×1016
T2≈7.61×102day2
T≈√7.61×102≈27.57days
The time period of the Moon's revolution around the Earth is approximately 27.57days.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Rate constant of two reactions are given below. Identifying their order of reaction
k=5.3×10−2Lmol−1s−1
k=3.8×10−4s−1A(i) second order, (ii) first orderB(i) first order, second orderC(i) zero order, (ii) first orderD(i) second order, (ii) zero order - Question 2 - Select One
The velocity constant of a reaction at 290 K was found to be 3.2×10−3s−1. When the temperature is raised to 310 K, it will be about
A6.4×10−3B3.2×10−4C9.6×10−3D1.28×10−2 - Question 3 - Select One
The velocity constant of a reaction at 290 K was found to be 3.2×10−3s−1. When the temperature is raised to 310 K, it will be about
A6.4×10−3B3.2×10−4C9.6×10−3D1.28×10−2
The distance of the planet Jupiter from the Sun is 5.2 times that of the Earth. Find the period of Jupiter's revolution around the Sun.
View SolutionThe rate constant for a second order reaction is given by k=(5×1011)e−29000k/T. The value of Ea will be:
View SolutionCalculate the distance from the earth to the point where the gravitational field due to the earth and the moon cancel out. Given that the earth-moon distance is 3.8×108m and the mass of earth is 81 times that of moon.
View SolutionThe Earth and Jupiter are two planets of the sun. The orbital radius of the earth is 107m and that of Jupiter is 4×107m If the time period of revolution of earth is T=365 days find time period of revolution of the Jupiter
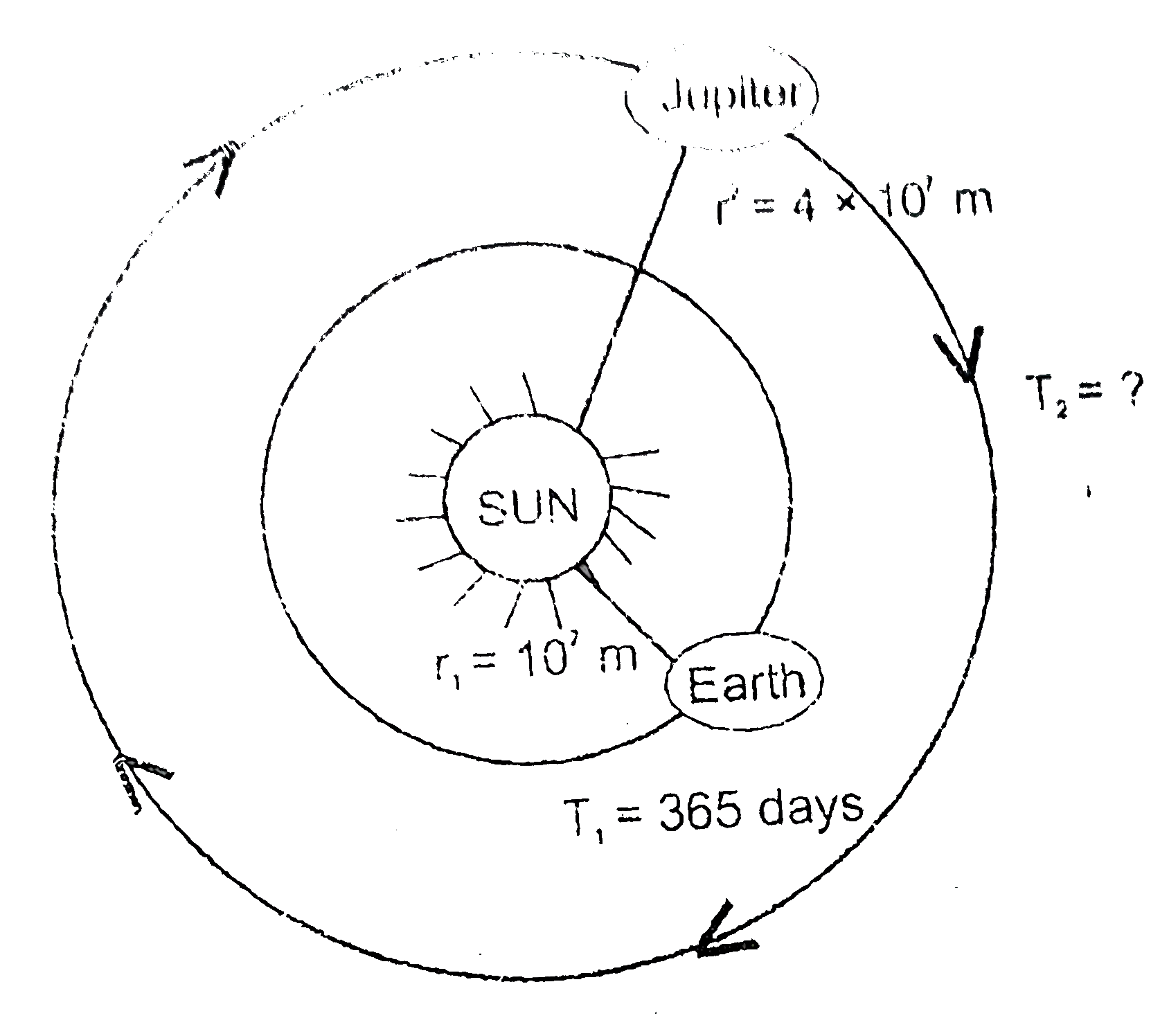 .View Solution
.View SolutionThe velocity constant of a reaction at 290 K was found to be 3.2×10−3s−1. When the temperature is raised to 310 K, it will be about
View Solution

