If 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Relative density of mercury = 13.6).
To solve the problem of finding the difference in the levels of mercury in the two arms of the tube after pouring 15 cm of water and spirit into their respective arms, we will follow these steps:
Step 1: Identify the heights of the liquids
We start with the initial heights of the liquids in each arm of the tube:
- The height of water in one arm (h1) is initially 10 cm, and we add 15 cm of water, making it:
h1=10cm+15cm=25cm
- The height of spirit in the other arm (h2) is initially 12.5 cm, and we add 15 cm of spirit, making it:
h2=12.5cm+15cm=27.5cm
Step 2: Calculate the pressure exerted by each liquid
Next, we calculate the pressure exerted by the columns of water and spirit:
- The density of water (ρ1) is 1 g/cm³.
- The density of spirit (ρ2) is 0.8 g/cm³.
- The density of mercury (ρ3) is 13.6 g/cm³.
Using the formula for pressure P=ρ⋅h⋅g (where g is the acceleration due to gravity, which we can cancel out later), we find:
- The pressure exerted by the water column:
P1=ρ1⋅h1=1g/cm3⋅25cm=25g/cm2
- The pressure exerted by the spirit column:
P2=ρ2⋅h2=0.8g/cm3⋅27.5cm=22g/cm2
Step 3: Calculate the difference in pressure
Now, we calculate the difference in pressure between the two columns:
ΔP=P1−P2=25g/cm2−22g/cm2=3g/cm2
Step 4: Relate the pressure difference to the height of mercury
The pressure difference will cause a height difference in the mercury column. The pressure exerted by the mercury column can be expressed as:
Pmercury=ρ3⋅h⋅g
Setting the pressure difference equal to the pressure exerted by the mercury:
ρ3⋅h=ΔP
Substituting the values:
13.6g/cm3⋅h=3g/cm2
Step 5: Solve for the height difference (h)
Now we can solve for h:
h=3g/cm213.6g/cm3=0.221cm
Conclusion
Thus, the difference in the levels of mercury in the two arms of the tube is:
Difference=0.221cm
---
We start with the initial heights of the liquids in each arm of the tube:
- The height of water in one arm (h1) is initially 10 cm, and we add 15 cm of water, making it:
h1=10cm+15cm=25cm
- The height of spirit in the other arm (h2) is initially 12.5 cm, and we add 15 cm of spirit, making it:
h2=12.5cm+15cm=27.5cm
Next, we calculate the pressure exerted by the columns of water and spirit:
- The density of water (ρ1) is 1 g/cm³.
- The density of spirit (ρ2) is 0.8 g/cm³.
- The density of mercury (ρ3) is 13.6 g/cm³.
- The pressure exerted by the water column:
P1=ρ1⋅h1=1g/cm3⋅25cm=25g/cm2
- The pressure exerted by the spirit column:
P2=ρ2⋅h2=0.8g/cm3⋅27.5cm=22g/cm2
Now, we calculate the difference in pressure between the two columns:
ΔP=P1−P2=25g/cm2−22g/cm2=3g/cm2
The pressure difference will cause a height difference in the mercury column. The pressure exerted by the mercury column can be expressed as:
Pmercury=ρ3⋅h⋅g
Setting the pressure difference equal to the pressure exerted by the mercury:
ρ3⋅h=ΔP
Substituting the values:
13.6g/cm3⋅h=3g/cm2
Now we can solve for h:
h=3g/cm213.6g/cm3=0.221cm
Thus, the difference in the levels of mercury in the two arms of the tube is:
Difference=0.221cm
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE
31 Videos
- LAWS OF MOTION BOOK - NCERT ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EXERCISE
40 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
21 Videos
Similar Questions
A u tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are at the same levels with 10 cm of water in one arm and 12.5 cm of spirit on the other arm as shown. If 15 cm of water and spirit each are further poured into the respective arms of the tube. Difference in the level of mercury in the two arms is (Take, relative density of mercury = 13.6, relative density of spirit=0.8)
View SolutionBy taking two J- tubes at constant temperature what is the difference in the levels of mercury in two columns ?
View Solution
Knowledge Check
in previous question, if 15 cm of water and spirit each are further poured into the respective arms of the tube. Difference in the level of mercury in the two arms is (Take, relvative density of mercury = 13.6)
A0.20 cmB0.22 cmC0.27 cmD0.26 cm
In a constant volume gas thermometer, the pressure of the working gas is measured by the difference in the levels of mercury in the two arms of a U-tube connected to the gas at one end. When the bulb is placed at the room temperature 27.00C, the mercury column in the arm open to atmosphere stands 5.00cm above the level of mercury in the other arm. When the bulb is placed in a hot liquid, the difference of mercury levels becomes 45.0cm. Calculate the temperature of the liquid. (Atmospheric pressure =75.0cm of mercury).
View SolutionIn a constant volume gas thermometer, the pressure of the working gas is measured by the differenced in the levels of mercury in the two arms of a U-tube connected to the gas at one end. When the bulb is placed at the room temperature 27.00C, the mercury column in the arm open to atmosphere stands 5.00cm above the level of mercury in the other arm. When the bulb is placed in a hot liquid, the difference of mercury levels becomes 45..0Cm. Calculate the temperature of the liquid. (Atmospheric pressure =75.0cm of mercury).
View SolutionA simple U tube contains mercury to the same level in both of its arms. If water is poured to a height of 13.6 cm in one arm, how much will be the rise in mercury level in the other arm ?
Given : density of mercury = 13.6×103kg m−3 and density of water = 103kg m−3.
View SolutionAn open U-tube contains mercury. When 11.2 cm of water is poured into one of the arms of the tube, how high does the mercury rise in the other arm from its initial level ?
View SolutionA manometer tube contains mercury of density 13.6×103 kg m−3. What difference in the levels of mercury in the two arms is indicated by a gauge pressure of 1.03×105Pa?
View SolutionThe velocity head of a stream of water is equal to 20 cm of mercury column. What is the velocity of flow in the stream ? The relative density of mercury is 13.6. (g=9.8ms−2)
View SolutionTwo communicating vessels contain mercury. The diameter of one vessel in n times larger then the diameter of the other. A column of water of height h is poured into the left vessel. The mercury level will rise in the right hand vessel (s = relative density of mercury and ρ = density of water) by
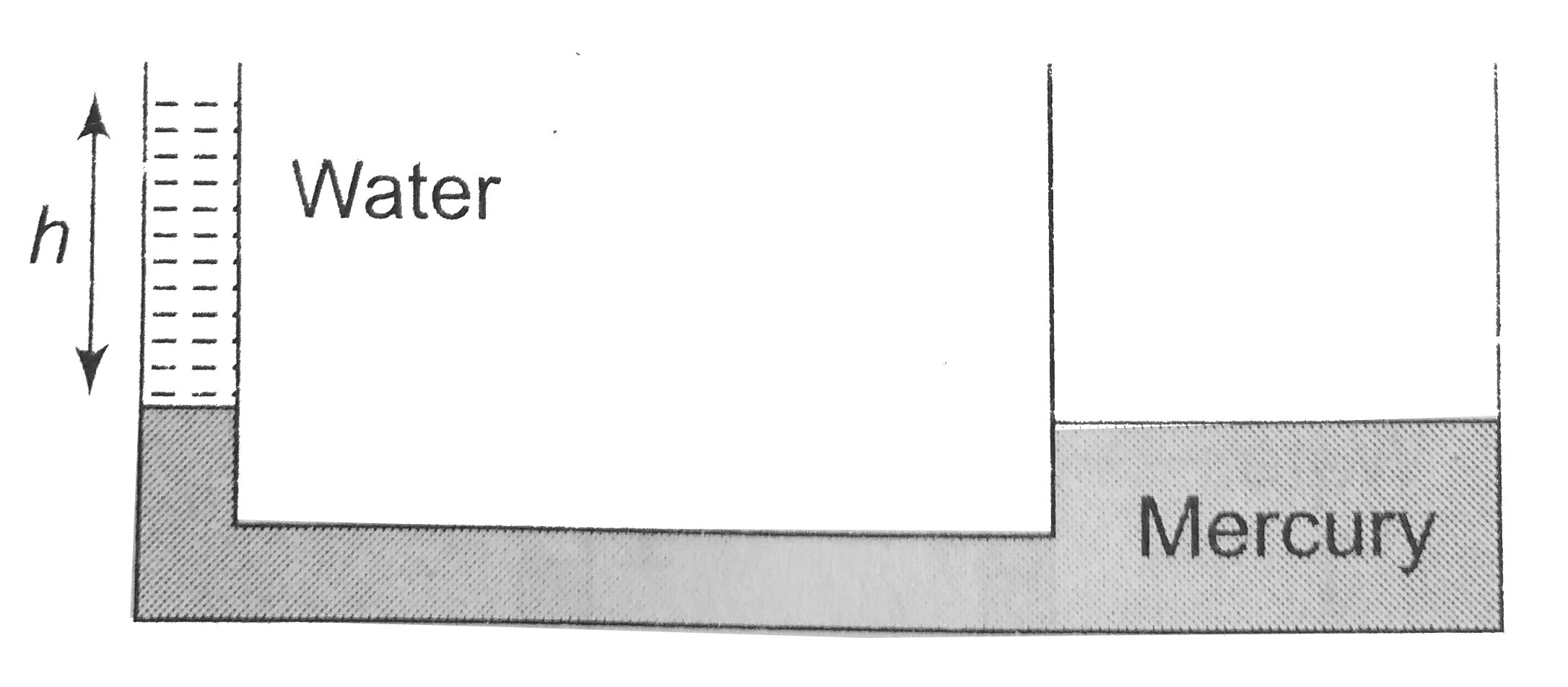
View Solution
