If a charged particle is a plane perpendicular to a uniform magnetic field with a time period T Then
T2∝r3
T2∝r
T∝r2
T∝r0
The correct Answer is:D
To solve the problem step-by-step, we start by analyzing the motion of a charged particle in a magnetic field.
1. Understanding the Motion:
A charged particle moving in a plane perpendicular to a uniform magnetic field will undergo circular motion due to the magnetic force acting on it.
2. Applying Lorentz Force:
The magnetic force (Lorentz force) acting on the charged particle is given by:
F=q(v×B)
Since the velocity v and magnetic field B are perpendicular, we can simplify this to:
F=qvB
3. Centripetal Force:
For circular motion, the centripetal force required to keep the particle moving in a circle is given by:
F=mv2r
where m is the mass of the particle, v is its velocity, and r is the radius of the circular path.
4. Setting Forces Equal:
Since the magnetic force provides the centripetal force, we can set these two expressions for force equal to each other:
qvB=mv2r
5. Cancelling v:
We can cancel v from both sides (assuming v≠0):
qB=mvr
6. Expressing Velocity:
The velocity v can also be expressed in terms of the time period T of the circular motion. The distance traveled in one complete circle (circumference) is 2πr, so:
v=2πrT
7. Substituting Velocity:
Substituting this expression for v back into the equation gives:
qB=m(2πr/T)r
Simplifying this, we get:
qB=2πmT
8. Solving for Time Period T:
Rearranging the equation to solve for T:
T=2πmqB
9. Analyzing the Relationship:
From the equation T=2πmqB, we see that T is independent of r (the radius of the circular path). This means:
T∝r0
Conclusion:
Thus, the correct answer is that the time period T is proportional to r0, which corresponds to option D.
A charged particle moving in a plane perpendicular to a uniform magnetic field will undergo circular motion due to the magnetic force acting on it.
The magnetic force (Lorentz force) acting on the charged particle is given by:
F=q(v×B)
Since the velocity v and magnetic field B are perpendicular, we can simplify this to:
F=qvB
For circular motion, the centripetal force required to keep the particle moving in a circle is given by:
F=mv2r
where m is the mass of the particle, v is its velocity, and r is the radius of the circular path.
Since the magnetic force provides the centripetal force, we can set these two expressions for force equal to each other:
qvB=mv2r
We can cancel v from both sides (assuming v≠0):
qB=mvr
The velocity v can also be expressed in terms of the time period T of the circular motion. The distance traveled in one complete circle (circumference) is 2πr, so:
v=2πrT
Substituting this expression for v back into the equation gives:
qB=m(2πr/T)r
Simplifying this, we get:
qB=2πmT
Rearranging the equation to solve for T:
T=2πmqB
From the equation T=2πmqB, we see that T is independent of r (the radius of the circular path). This means:
T∝r0
Thus, the correct answer is that the time period T is proportional to r0, which corresponds to option D.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
Knowledge Check
When a charged particle is projected perpendicular to a uniform magnetic field, it describes a circular path in which :
Aits speed remains constant.Bits velocity remains constant.Cits momentum remains constant.Dits kinetic energy increases.
Assertion When a charged particle moves perpendicular to a uniform magnetic field then its momentum remains constant.
Reason Magnetic force acts perpendicular to the velocity of the particle.
View SolutionA particle is projected in a plane perpendicular to a uniform magnetic field. The area bounded by the path described by the particle is proportional to
View SolutionA particle is projected in a plane perpendicular to a uniform magnetic field. The area bounded by the path described by the particle is proportional to
View SolutionA charged particle is projected perpendicular to uniform magnetic field. It describes a circle, the quantities which are inversely proportional to specific charge are
i) Radius ii) K. E
iii) Time period iv) Momentum
View SolutionParticles 1, 2 and 3 are moving perpendicular to a uniform magnetic field, then particle
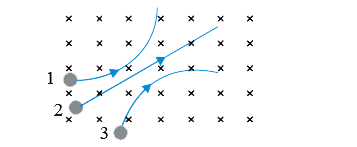
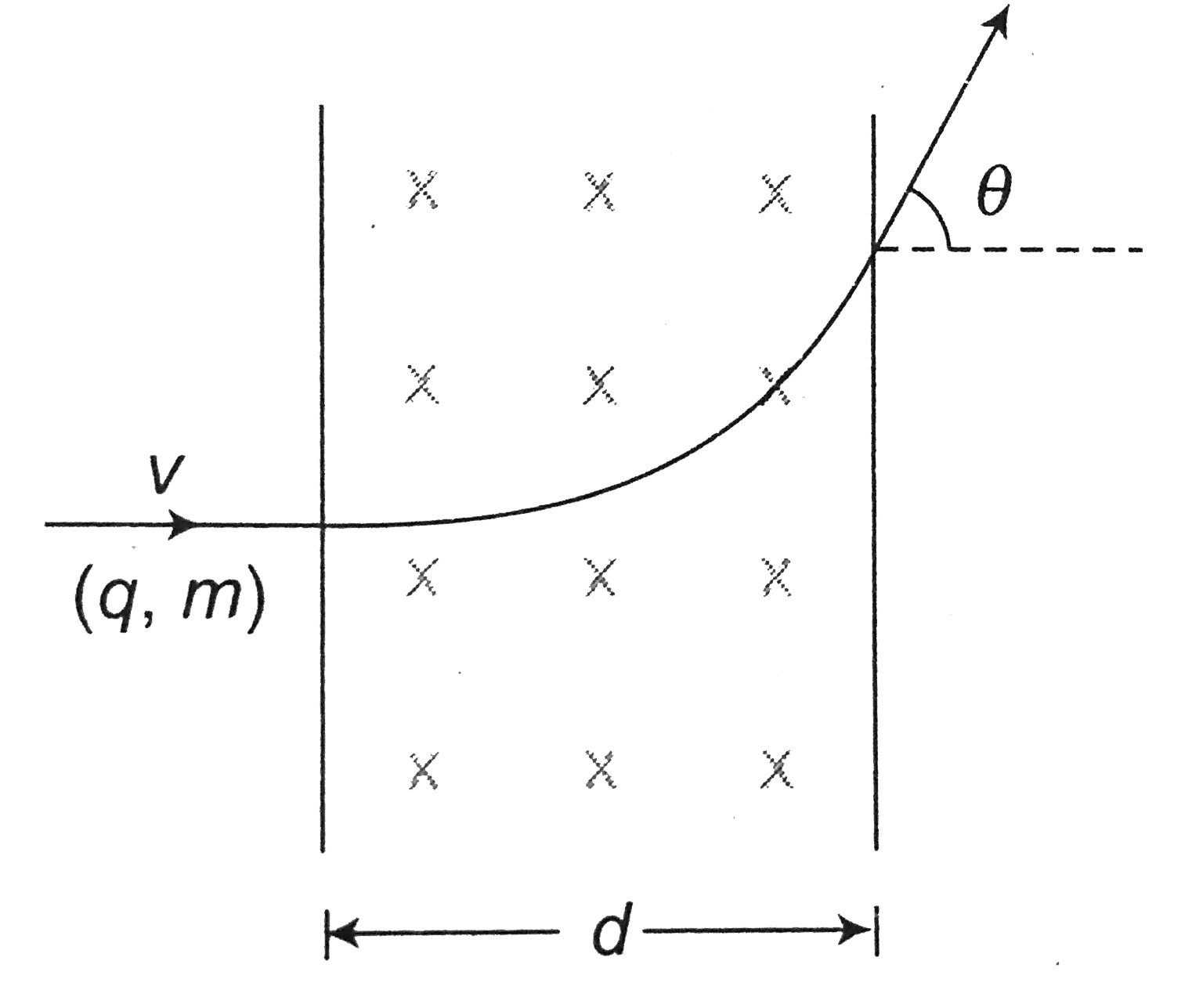
View SolutionA charged particle (q,m) enters perpendicular in a uniform magnetic field B and comes out field as shown. Find the angle of deviation θ for particle to cross magnetic field will be
View SolutionA proton and an alpha particle move in circular paths in a plane perpendicular to a uniform magnetic field. If the kinetic energy of the two particles is equal, the ratio of the radii of their paths is _________.
View Solution
