If a charged particle of charge to mass ratio $(\frac{q}{m}) = α$ centers in a magnetic field of strength B at a speed $v = (2 α d) (B),$ then

A

angle subtended by the path of charge particle in magnetic field at the centre of circular path is $2 π$ .

B

the charge will move on a circular path and then will come out from magnetic field at some distance from the point of insertion.

C

the time for which particle will be in the magnetic field is $\frac{2 π}{α B}$

D

angle subtended by the path of charge particle in magnetic field at the centre of circular path is $π / 2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$r = \frac{m v}{q B} = \frac{v}{B α} = \frac{(2 α d) (B)}{(B α)} = 2 d$

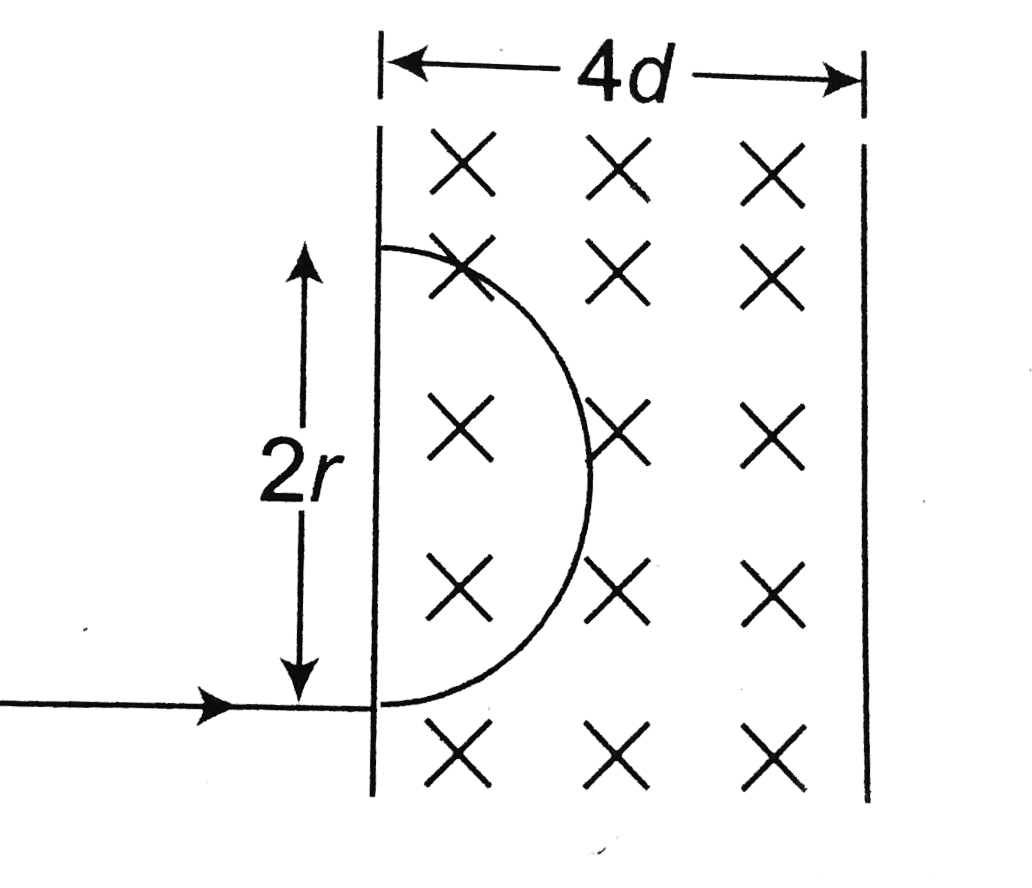
i.e., the electron will move
outafter travelling on a
semicircular path of radius $r = 2 d$ .

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If a charge particle of charge q , mass m , moves in a circular path in magnetic field of induction B , under a potential of V volts then radius of circular path is
A $\sqrt{\frac{2 m V}{q}}$
B $\frac{B}{1} \sqrt{\frac{2 m V}{q}}$
C $\frac{1}{B} \sqrt{\frac{2 m V}{q}}$
D $\frac{1}{B^{2}} \sqrt{\frac{2 m V}{q}}$
Question 2 - Select One or More
A charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle $θ$ with the field. The frequency of revolution of the particle
ADepends on the angle $θ$
BIs independent of the angle $θ$
CIs proportional to the specific charge q/m of the particle
DIs inversely proportional to the value of B
Question 3 - Select One
A charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B. The frequency of revolution is
A $\frac{3 B q}{2 π m}$
B $\frac{3 B q}{2 π m}$
C $\frac{2 π m}{2 B q}$
D $\frac{B q}{2 π m}$

A2Z-SOURCE AND EFFECT OF MAGNETIC FIELD-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile