If a dielectric slab is introduced between the plates of a parallel plate capacitor after the battery is disconnected, then how do the following quantities change.
(i) Charge
(ii) Potential
(iii) Capacitance (iv) Energy.
To analyze how the introduction of a dielectric slab between the plates of a parallel plate capacitor affects various quantities, we will consider the following steps:
Given:
- A parallel plate capacitor with capacitance C.
- The capacitor is disconnected from the battery before the dielectric slab is introduced.
Definitions:
1. Capacitance (C): The ability of a capacitor to store charge per unit voltage, given by the formula:
C=QV
where Q is the charge and V is the potential difference.
2. Dielectric Constant (κ): A measure of a material's ability to store electrical energy in an electric field. The capacitance of a capacitor with a dielectric is given by:
C′=κC
where C′ is the new capacitance with the dielectric.
1. Charge (Q):
- When the capacitor is disconnected from the battery, the charge Q on the plates remains constant. This is because there is no path for charge to flow to or from the capacitor.
- Conclusion: The charge Q remains unchanged.
2. Potential (V):
- The potential difference across the capacitor can be expressed as:
V=QC
- When the dielectric slab is introduced, the capacitance increases to C′=κC. Since Q remains constant, the new potential V′ becomes:
V′=QC′=QκC=Vκ
- Conclusion: The potential V decreases.
3. Capacitance (C):
- The introduction of the dielectric increases the capacitance:
C′=κC
- Conclusion: The capacitance C increases.
4. Energy (U):
- The energy stored in a capacitor is given by:
U=12CV2
- After introducing the dielectric, the new energy U′ can be expressed as:
U′=12C′V′2=12(κC)(Vκ)2=12(κC)V2κ2=12CV2κ
- Since U=12CV2, we find that:
U′=Uκ
- Conclusion: The energy U decreases.
Summary of Changes:
- (i) Charge: Unchanged
- (ii) Potential: Decreases
- (iii) Capacitance: Increases
- (iv) Energy: Decreases
- A parallel plate capacitor with capacitance C.
- The capacitor is disconnected from the battery before the dielectric slab is introduced.
1. Capacitance (C): The ability of a capacitor to store charge per unit voltage, given by the formula:
C=QV
where Q is the charge and V is the potential difference.
C′=κC
where C′ is the new capacitance with the dielectric.
- When the capacitor is disconnected from the battery, the charge Q on the plates remains constant. This is because there is no path for charge to flow to or from the capacitor.
- Conclusion: The charge Q remains unchanged.
- The potential difference across the capacitor can be expressed as:
V=QC
- When the dielectric slab is introduced, the capacitance increases to C′=κC. Since Q remains constant, the new potential V′ becomes:
V′=QC′=QκC=Vκ
- Conclusion: The potential V decreases.
- The introduction of the dielectric increases the capacitance:
C′=κC
- Conclusion: The capacitance C increases.
- The energy stored in a capacitor is given by:
U=12CV2
- After introducing the dielectric, the new energy U′ can be expressed as:
U′=12C′V′2=12(κC)(Vκ)2=12(κC)V2κ2=12CV2κ
- Since U=12CV2, we find that:
U′=Uκ
- Conclusion: The energy U decreases.
- (i) Charge: Unchanged
- (ii) Potential: Decreases
- (iii) Capacitance: Increases
- (iv) Energy: Decreases
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS6videos
ELECTROSTATICS AND CURRENT ELECTRICITY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - NUMERICALS49videos
ELECTROSTATICS AND CURRENT ELECTRICITY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (2 MARKS)59videos
ELECTROSTATICS AND CURRENT ELECTRICITY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS7videos
ELECTRONIC DEVICES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C19videos
SAMPLE QUESTION PAPER 2019
Similar Questions
Two identical capacitors are connected as shown in fignre. A dielectric slab is introduced between the plates of one of the capacitors so as to fill the gap, the battery remaining connected. What will be the capacitance, the charge, potential difference and stored energy for each capacitor?
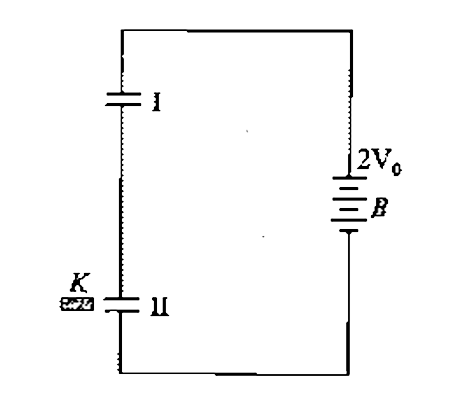 View Solution
View SolutionTwo identical capacitors are connected as shown. A dielectric slab Is introduced between the plates of one of the capacitors so as to fill the gap, the battery remaining connected. Compare the capacitance, the charge, potential difference and stored energy of each capacitor before and arter introducting of dielectric slab.
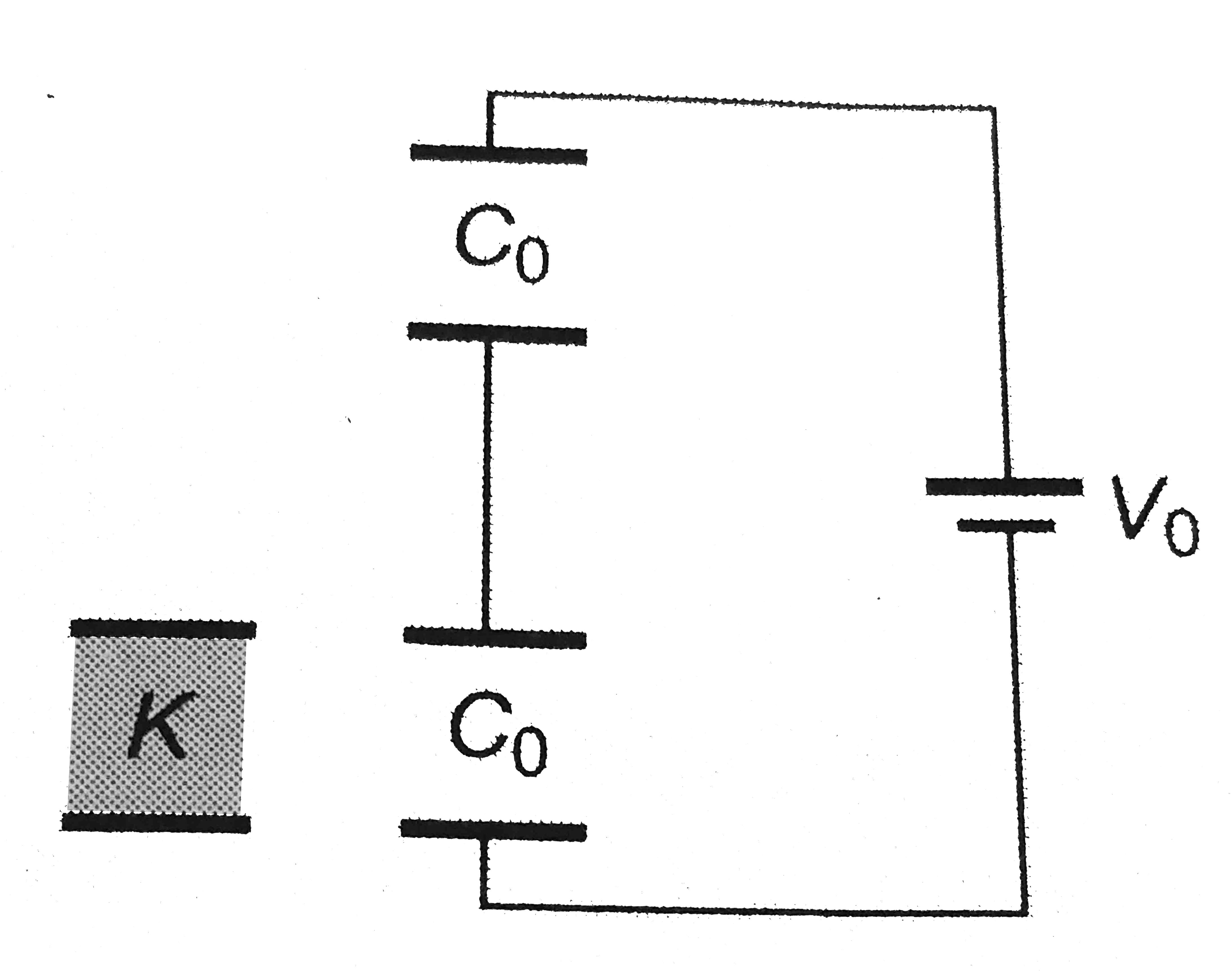 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreases - Question 2 - Select One
When a dielectric is introduced between the plates of a charged parallel plate capacitor, whichi one of the following will not change?
A1.ChargeB2. Potential differenceC3. Electric fieldD4. Energy - Question 3 - Select One
When a dielectric material is introduced between the plates of a charged condenser, after disconnected the battery the electric field between the plates
AdecreaseBincreasesCdoes not changeDmay increase or decrease
Explain why the capacitance of a parallel plate capacitor increases when a dielectric slab is introduced between the plates.
View SolutionA parallel plate capcitor of capacitance C is charged to a potential V by a battery. Without disconencting the battery = distance between the plates of capacitor is triple and a dielectric medium of K = 10 is introduced between the plates of capacitor. Explain giving reasons how will the following be affected ?
(a) Capacitance of capacitor
(b) Charge on capacitor
(c ) Energy density of capacitor.View SolutionIf a dielectric slab of thickness 5 mm and dielectric constant K=6 is introduced between the plates of a parallel plate air capacitor, with plate separation of 8 mm, then its capacitance is
View SolutionThe plates of a parallel plate capacitor are charged by a battery and the battery is disconnected after the charging. Now, the plates are placed as shown in the figure. Then (plates are not parallel to each other).
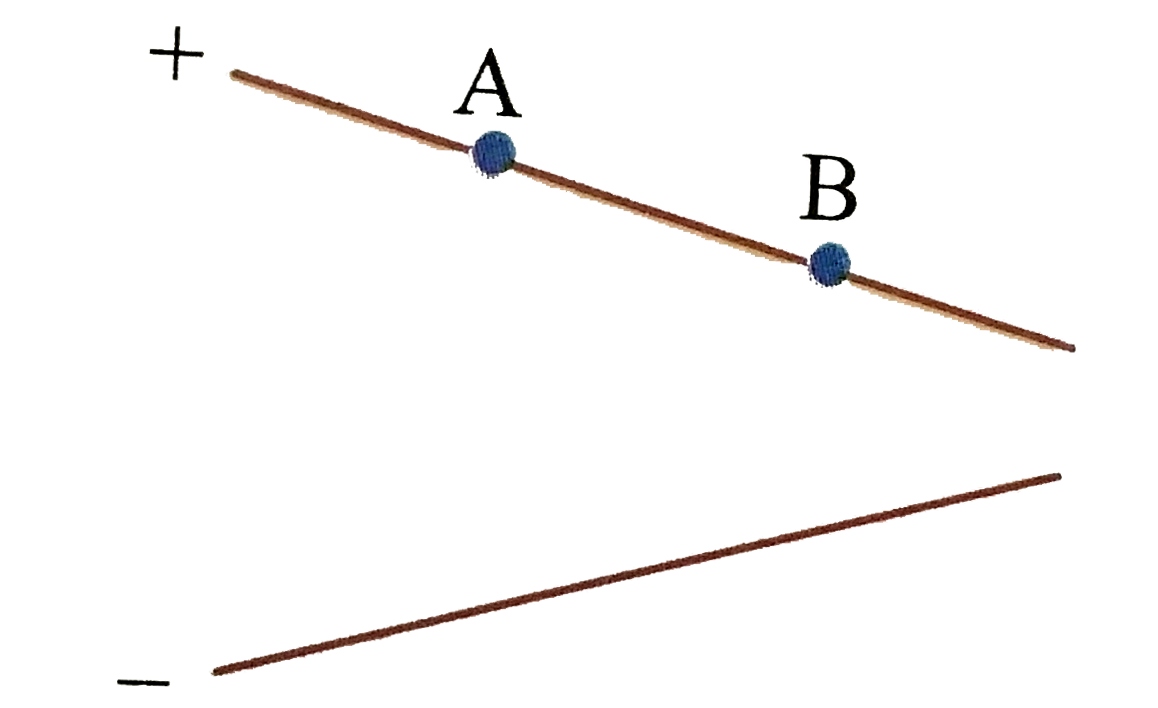 .View Solution
.View SolutionSpace between the plates of a parallel plate capacitor is filled with a dielectric slab. The capacitor is charged and then the supply is disconnected to it. If the slab is now taken out then
View Solution

