If a force is applied to an object, away from its centre of mass, it tends to rotate the object.
To understand how a force applied away from the center of mass of an object causes it to rotate, we can break down the explanation into clear steps:
1. Identify the Object and Its Center of Mass:
- Consider an object with a defined center of mass (point O). The center of mass is the point where the mass of the object is concentrated.
2. Apply a Force:
- Imagine applying a force (F) at a point that is not at the center of mass, but rather at a distance (r) away from it. This force can be directed in any direction.
3. Understand the Concept of Torque:
- When a force is applied at a distance from the center of mass, it creates a rotational effect known as torque (τ). Torque is calculated using the formula:
τ=r×F
- Here, r is the distance from the center of mass to the point where the force is applied, and F is the magnitude of the force.
4. Direction of Torque:
- The direction of the torque depends on the direction of the applied force and the position vector (r). The torque will cause the object to rotate about its center of mass.
5. Resulting Motion:
- As a result of the torque, the object will begin to rotate around its center of mass. The angular acceleration produced will depend on the magnitude of the torque and the moment of inertia of the object.
6. Conclusion:
- Therefore, applying a force away from the center of mass results in a rotational motion due to the torque generated by the force.
- Consider an object with a defined center of mass (point O). The center of mass is the point where the mass of the object is concentrated.
- Imagine applying a force (F) at a point that is not at the center of mass, but rather at a distance (r) away from it. This force can be directed in any direction.
- When a force is applied at a distance from the center of mass, it creates a rotational effect known as torque (τ). Torque is calculated using the formula:
τ=r×F
- Here, r is the distance from the center of mass to the point where the force is applied, and F is the magnitude of the force.
- The direction of the torque depends on the direction of the applied force and the position vector (r). The torque will cause the object to rotate about its center of mass.
- As a result of the torque, the object will begin to rotate around its center of mass. The angular acceleration produced will depend on the magnitude of the torque and the moment of inertia of the object.
- Therefore, applying a force away from the center of mass results in a rotational motion due to the torque generated by the force.
Topper's Solved these Questions
- FORCE AND PRESSURE BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - Exercises (Section I) Choose the correct option to fill in the blank.
6 Videos
- FORCE AND PRESSURE BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - Exercises (Section II) Give reasons for the following
6 Videos
- FORCE AND PRESSURE BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - Exercises (Section I) Choose the correct option
6 Videos
- ENERGYBOOK - ICSECHAPTER - ENERGYEXERCISE - THEME ASSIGNMENT
4 Videos
- HEAT TRANSFER BOOK - ICSECHAPTER - HEAT TRANSFER EXERCISE - Picture Study
2 Videos
Similar Questions
The inertia of an object tends to cause the object
View SolutionWhen force applied on an object causes it to moves in the direction of force
View SolutionWhen a force is applied on an object and if the body moves in the direction of applied force, work is said to be done.
View SolutionTwo objects are at rest on a level frictionless surface. The objects are not connected. A force F is applied to one of the objects, which then moves with acceleration a. Mark the correct statement(s).
View SolutionTwo object are initially at rest on a frictionless surface. Object 1 has a greater mass than object 2. The same constant force start to act on each object. The force is removed from each object after it accelerates over a distance d. after the force is removed from both objects, which statement is correct (p:momentum, K: kinetic energy)?
View SolutionA force F=(xˆi+2yˆj)N is applied on an object of mass 10 kg, Force displaces the object from position A(1, 0) m to position B(3, 3) m then the work done by the force is (x and y are meter)
View Solution_E01_059_Q01.png)
An object of weight W has a uniform rectangular cross section of a x2a and density of 0.25g/cm3 part of it is immersed in water and the rectangle is tilted by 45∘− while one of its corners is just at the water surface find the torque of the buoyancy force to the centre of mass of the object.
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
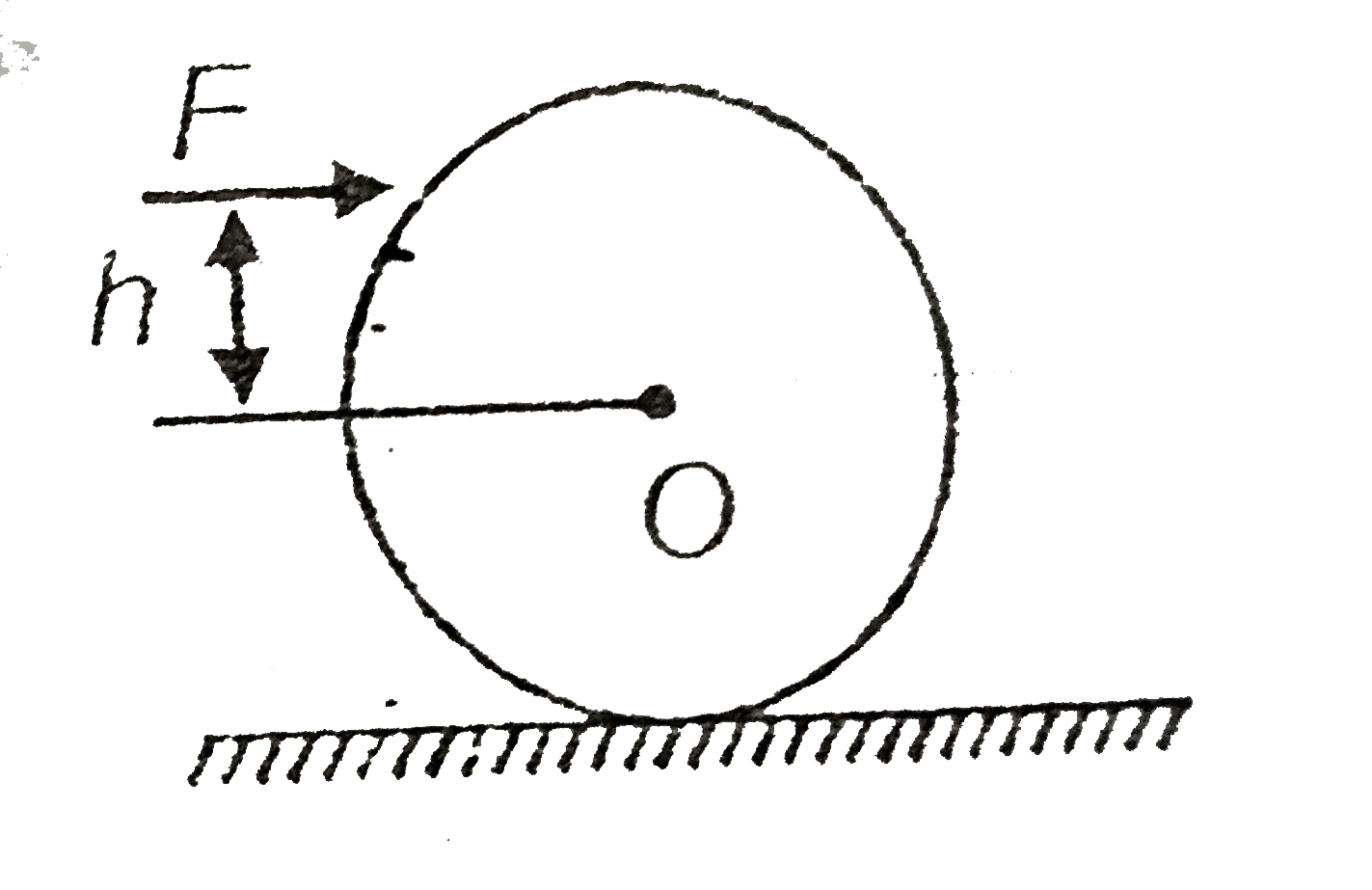
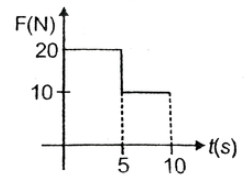
View SolutionForce is applied on an object of mass 2 kg at rest on a frictionless horizontal surface as shown in the graph. The speed of object at t=10 s will be
View SolutionIf an object is placed at the centre of a glass sphere and it is seen from outside, then prove that its virtual image is also formed at centre.
View Solution
