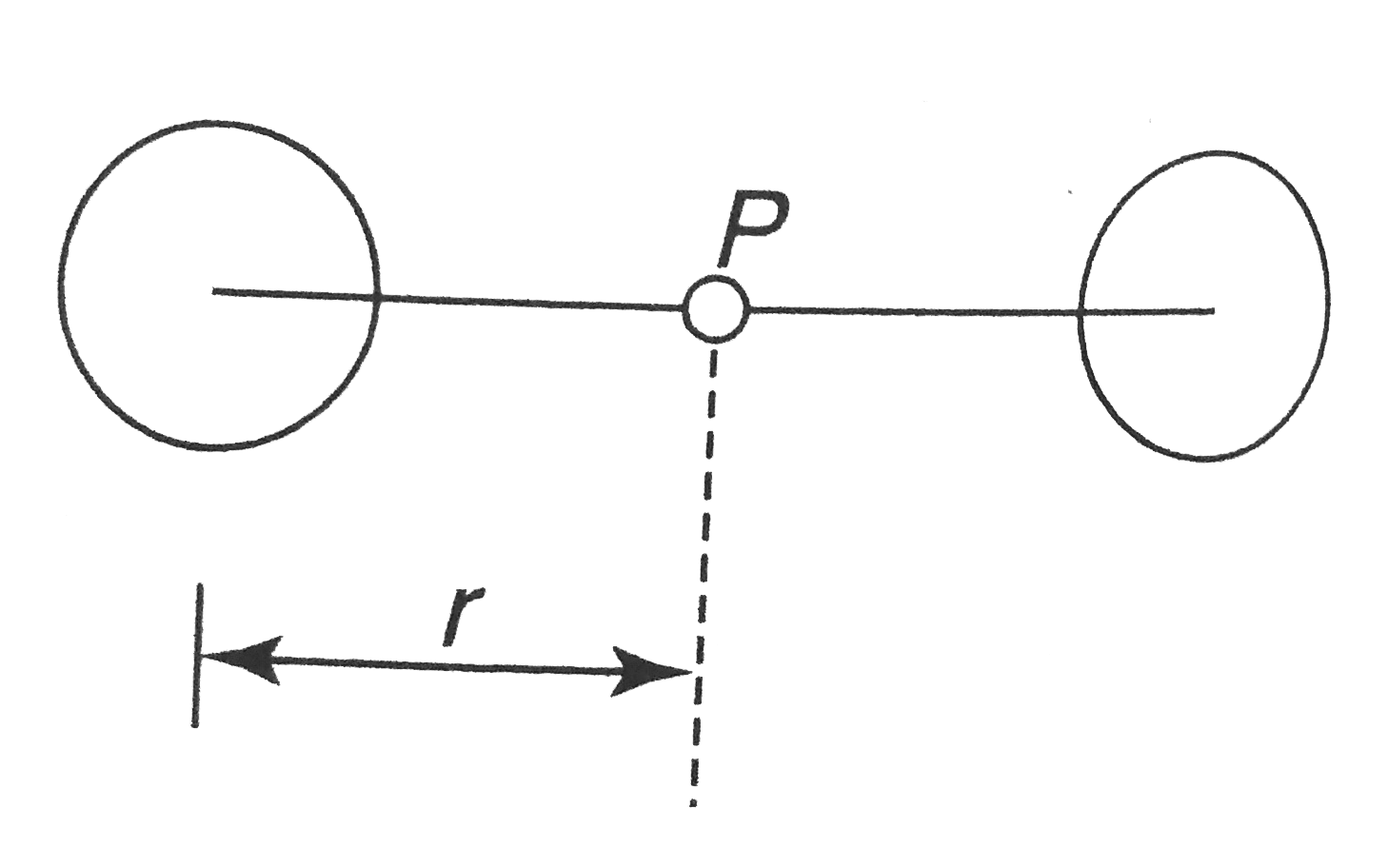
If a particles of mass $m$ is projected with minimum velocity form the surface of a star with kinetic energy $\frac{K_{1} G M m}{a}$ and potential energy at surface of the star $\frac{K_{2} G M m}{a}$ towards the star of same mass $m$ and radius $a$ ( $K_{1}$ and $K_{2}$ are constant) to reach the other star. Find the distance between the centre of the two stars:

$\frac{2 a}{(K_{2} - K_{1})}$

$\frac{4 a}{(K_{2} - K_{1})}$

$\frac{2 a}{(K_{1} - K_{2})}$

$\frac{a}{(K_{1} - K_{2})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Since the mass and radius of two stars are same, point $P$ at which gravitational force will be equal, will be at equal distance (say $r$ ) from centre of each star. The particle should be projected to cross $P$ , beyond which the particle will be attracted towards the other star.
$K E = P E$ of body at $P$ -PE at surface of the star
$\frac{K_{1} G M m}{a} = [- \frac{G M m}{r} - \frac{G M m}{r}] - [- K_{2} \frac{G M m}{a}]$
On solving, $r = \frac{2 a}{(K_{2} - K_{1})} 2 r = \frac{4 a}{(K_{2} - K_{1})}$

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A particle is projected from the surface of one star towards other star of same radius $a$ and mass with such a minimum velocity $K \sqrt{\frac{G M}{a}}$ , so that it is attracted towards other star. Find the value of $K$ if two stars are $2 r$ distance apart:

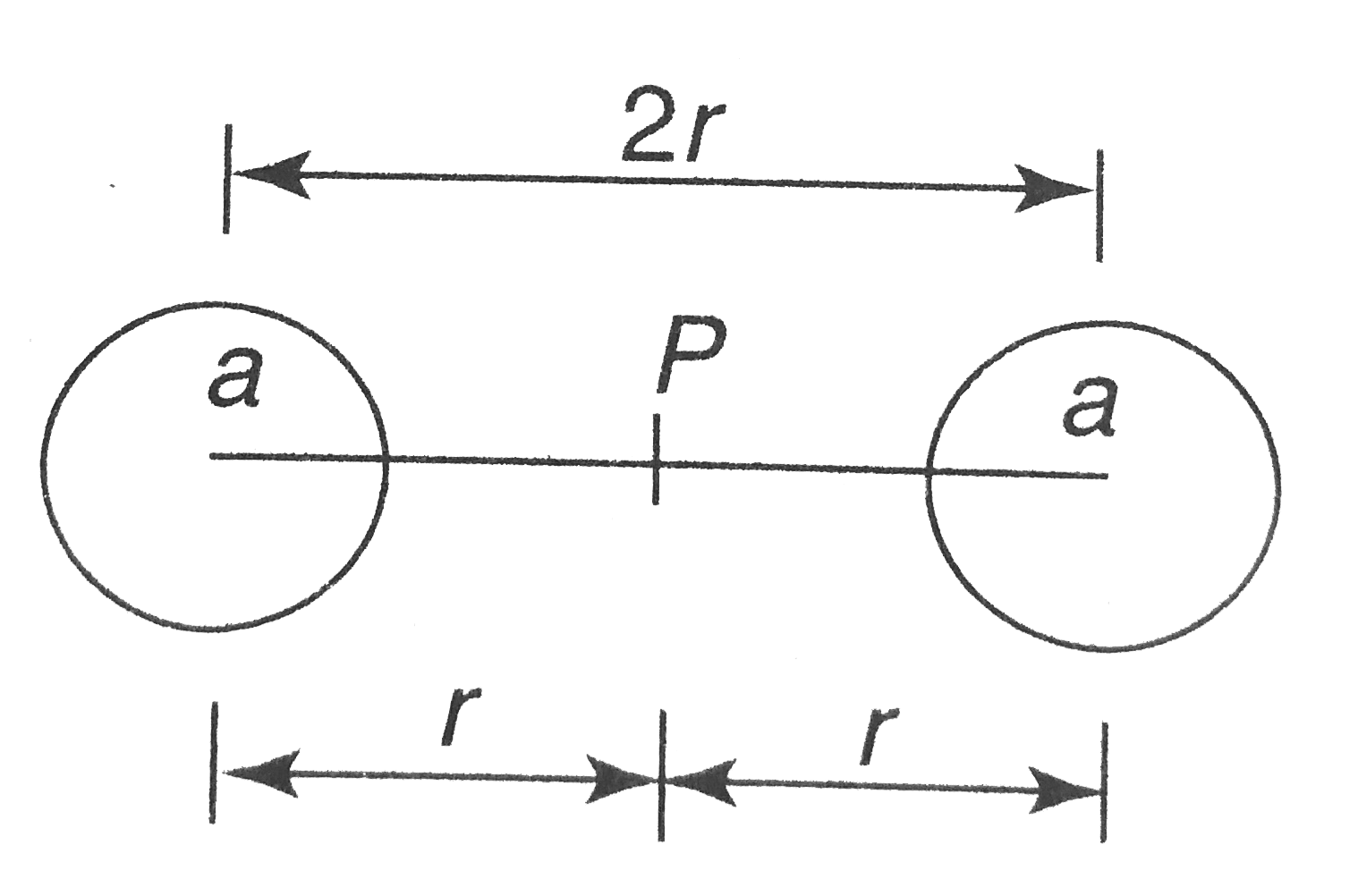A $\frac{2 (r - a)}{{[r (2 r - a)]}^{1 / 2}}$
B $\frac{2 (r - a)}{{[r (r - a)]}^{1 / 2}}$
C $\frac{r - a}{{[r (r - a)]}^{1 / 2}}$
D $\frac{r + a}{{[r (r - a)]}^{1 / 2}}$
Question 2 - Select One
Two stars bound together by gravity orbit othe because of their mutual attraction. Such a pair of stars is referred to as a binary star system. One type of binary system is that of a black hole and a companion star. The black hole is a star that has cullapsed on itself and is so missive that not even light rays can escape its gravitational pull therefore when describing the relative motion of a black hole and companion star, the motion of the black hole can be assumed negligible compared to that of the companion.
The orbit of the companion star is either elliptical with the black hole at one of the foci or circular with the black hole at the centre. The gravitational potential energy is given by $U = - G m M / r$ where G is the universal gravitational constant, m is the mass of the companion star, M is the mass of the black hole, and r is the distance between the centre of the companion star and the centre of the black hole. Since the gravitational force is conservative. The companion star and the centre of the black hole, since the gravitational force is conservative the companion star's total mechanical energy is a constant. Because of the periodic nature of of orbit there is a simple relation between the average kinetic energy $< K >$ of the companion star Two special points along the orbit are single out by astronomers. Parigee isthe point at which the companion star is closest to the black hole, and apogee is the point at which is the farthest from the black hole.
Q. For circular orbits the potential energy of the companion star is constant throughout the orbit. if the radius of the orbit doubles, what is the new value of the velocity of the companion star?
Ait is 1/2 of the old value
Bit is 1/ $\sqrt{2}$ of the old value
Cit is the same as old value
Dit is double the old value
Question 3 - Select One
Two stars bound together by gravity orbit othe because of their mutual attraction. Such a pair of stars is referred to as a binary star system. One type of binary system is that of a black hole and a companion star. The black hole is a star that has cullapsed on itself and is so missive that not even light rays can escape its gravitational pull therefore when describing the relative motion of a black hole and companion star, the motion of the black hole can be assumed negligible compared to that of the companion.
The orbit of the companion star is either elliptical with the black hole at one of the foci or circular with the black hole at the centre. The gravitational potential energy is given by $U = - G m M / r$ where G is the universal gravitational constant, m is the mass of the companion star, M is the mass of the black hole, and r is the distance between the centre of the companion star and the centre of the black hole. Since the gravitational force is conservative. The companion star and the centre of the black hole, since the gravitational force is conservative the companion star's total mechanical energy is a constant. Because of the periodic nature of of orbit there is a simple relation between the average kinetic energy $< K >$ of the companion star Two special points along the orbit are single out by astronomers. Parigee isthe point at which the companion star is closest to the black hole, and apogee is the point at which is the farthest from the black hole.
Q. Which of the following prevents the companion star from leaving its orbit and falling the black hole?
AThe centripetal force
Bthe gravitational force
CThe companion star's potential energy
DThe companion star's kinetc energy

A2Z-GRAVITATION-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

A particle is projected from the surface of one star towards other star of same radius a and mass with such a minimum velocity K√GMa, so that it is attracted towards other star. Find the value of K if two stars are 2r distance apart:

A2Z-GRAVITATION-Problems Based On Mixed Concepts

A particle is projected from the surface of one star towards other star of same radius $a$ and mass with such a minimum velocity $K \sqrt{\frac{G M}{a}}$ , so that it is attracted towards other star. Find the value of $K$ if two stars are $2 r$ distance apart: