If a particle of mass 'm' is projected from a surface of bigger sphere of mass '16M' and radius '2a' then find out the minimum velocity of the particle such that the particle reaches the surface of the smaller sphere of mass M and radius 'a'. Given that the distance between the centres of two spheres is 10 a.

Video Solution

Text Solution

Verified by Experts

When the particle is at the surface of bigger sphere it is attracted more by the bigger sphere and less by the smaller sphere. As it is projected the force of attraction from bigger sphere decreases and that from smaller sphere increass and thus the particle reaches the state of equilibrium at distance x from the centre smaller sphere

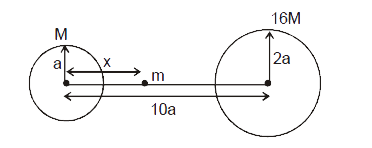
$\frac{G M m}{x^{2}} = \frac{G (16 M) m}{{(10 a - x)}^{2}}$
${(10 a - x)}^{2} = 16 x^{2}$

$10 a - x = 4 x \Rightarrow x = 2 a$
After this point the attraction on the particle from the smaller sphere becomes more than that from the bigger sphere and the particle will automatically move towards the smaller sphere. Hence the minimum velocity to reach the smaller sphere is the veloicty required to reach the equilibrium state according to energy conservation, we have,
$- \frac{G (16 M) m}{2 a} - \frac{G M m}{8 a} + \frac{1}{2} m v^{2}$
$= \frac{- G (16 M) m}{8 a} - \frac{G M m}{2 a}$
$v^{2} = \frac{45 G M}{4 a}$
$\Rightarrow v = \sqrt{\frac{45 G M}{4 a}}$

Updated on:21/07/2023