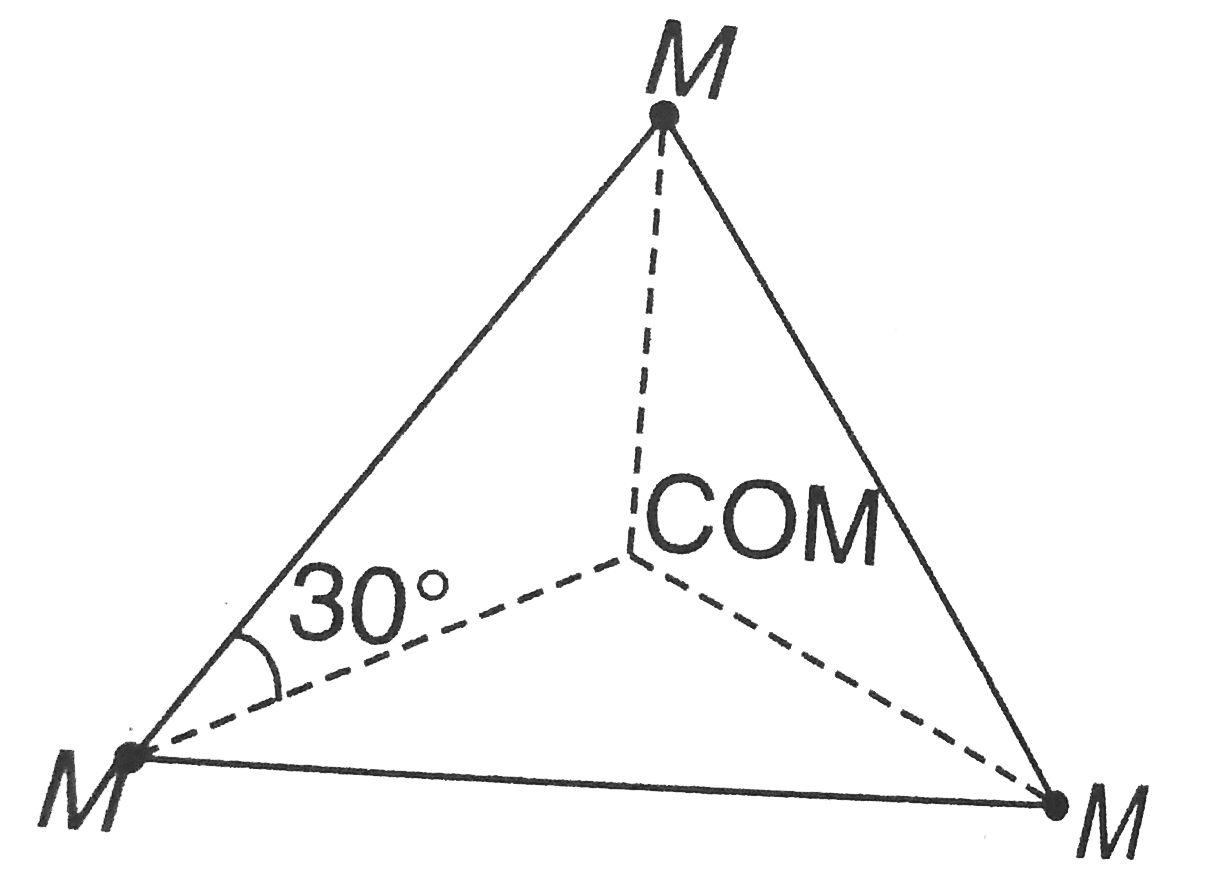
Three identical stars, each of mass $M$ , from an equilateral triangle (stars are positioned at the corners) that rotates around the centre of the triangle. The system is isolated and edge length of the triangle is $L$ . The amount of work done, that is required ot dismantle the system, is:

A

$\frac{3 G M^{2}}{L}$

B

$\frac{3}{2} \frac{G M^{2}}{L}$

C

$\frac{3}{4} \frac{G M^{2}}{L}$

D

$\frac{G M^{2}}{2 L}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Stars move around COM. Distance of each star form COM is $\frac{2}{3} \times L {\cos 30}^{\circ} = \frac{L}{\sqrt{3}}$
Force on each star $M$ due to the other two
$2 . \frac{G . M . M}{L^{2}} {\cos 30}^{\circ} = \sqrt{3} \frac{G M^{2}}{L^{2}}$
This acts as centripetal force.
Therefore, $\sqrt{3} \frac{G M^{2}}{L^{2}} = \frac{m v^{2}}{(L / \sqrt{3}) \Rightarrow V = \sqrt{\frac{G M}{L}}}$
To dismantle the system, energy equal to total energy of the system must be provided.
i.e. $3 \times \frac{1}{2} M V^{2} + (3 \times \frac{G M^{2}}{L}) = - \frac{3}{2} \frac{G M^{2}}{L}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three identical rods, each of mass $m$ and length $l$ , form an equaliteral triangle. Moment of inertia about one of the sides is

A $\frac{m l^{2}}{6}$
B $m l^{2}$
C $\frac{3 m l^{2}}{4}$
D $\frac{2 m l^{2}}{3}$
Question 2 - Select One
At each corner of an equilateral triangle identical charges are placed. Then at the centre of the triangle
Athe resultant electric intensity is zero
Bthe net potential is zero
Cboth electric intensity and potential are zero
Dneither electric intensity nor potential are zero
Question 3 - Select One or More
Each side of an equilateral triangle subtends an angle of $60^{\circ}$ at the top of a tower h m high located at the centre of the triangle. If a is the length of each side of the triangle, then
A $3 a^{2} = 2 h^{2}$
B $2 a^{2} = 2 h^{2}$
C $a^{2} = 3 h^{2}$
D $3 a^{2} = h^{2}$

A2Z-GRAVITATION-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile