A particle is projected from the surface of one star towards other star of same radius a and mass with such a minimum velocity K√GMa, so that it is attracted towards other star. Find the value of K if two stars are 2r distance apart:
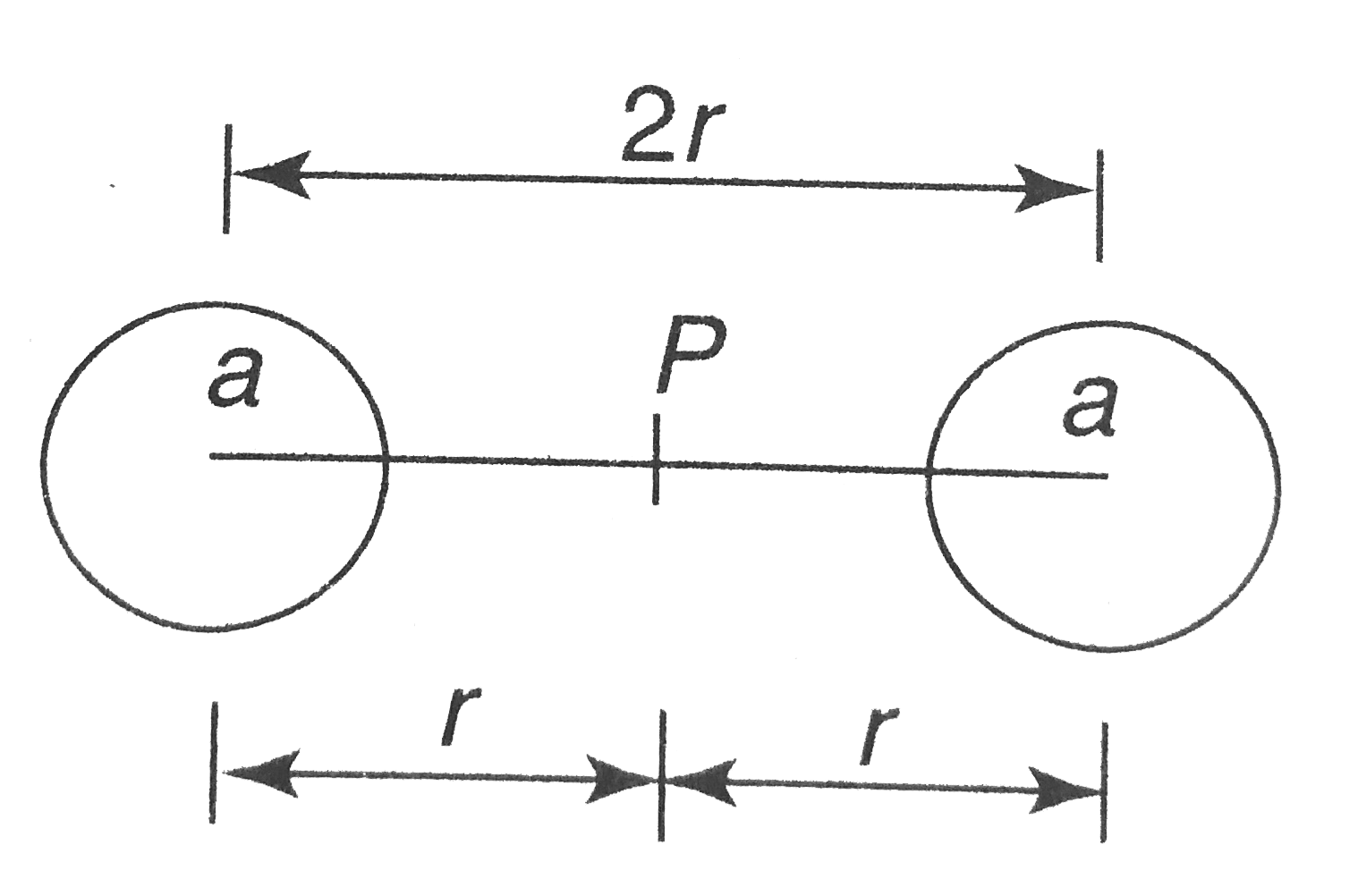
2(r−a)[r(2r−a)]1/2
2(r−a)[r(r−a)]1/2
r−a[r(r−a)]1/2
r+a[r(r−a)]1/2
The correct Answer is:A
12mv2min=[−GMmr−GMmr]
−[−GMm(2r−a)−GMma]
=2GMm(a2−2ar+r2)ar(2r−a)
or vmin=√GMa×2(r−a)[r(2r−a)]1/2
So, K=2(r−a)[r(2r−a)]1/2
Topper's Solved these Questions
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Assertion Reasoning
Explore 16 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:NEET Questions
Explore 42 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Motion Of Satellite
Explore 33 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Chapter Test
Explore 30 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:A2ZChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Chapter Test
Explore 29 Videos
Similar Questions
If a particle of mass 'm' is projected from a surface of bigger sphere of mass '16M' and radius '2a' then find out the minimum velocity of the particle such that the particle reaches the surface of the smaller sphere of mass M and radius 'a'. Given that the distance between the centres of two spheres is 10 a.
View SolutionA particle is projected upward from the surface of the earth (radius R ) with a kinetic energy equal to half the minimum value needed for it to escape. If the height it rises above the surface of the earth is h=kR, then find k.
View Solution
Knowledge Check
If a particles of mass m is projected with minimum velocity form the surface of a star with kinetic energy K1GMma and potential energy at surface of the star K2GMma towards the star of same mass m and radius a (K1 and K2 are constant) to reach the other star. Find the distance between the centre of the two stars:
A2a(K2−K1)B4a(K2−K1)C2a(K1−K2)Da(K1−K2)A pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M=2m The distance between the centres of the stars is d (d being large compared to the size of either star) .
The ratio of the angular momentum of the two stars about their common centre of mass (Lm/Lm) is .A1B2C4D9The angular velocity of rotation of star (of mass M and radius R ) at which the matter start to escape from its equator will be
A√2GM2RB√2GMgC√2GMR2D√2GRM
Distance between the centres of two stars is 10a. The masses of these stars are M and 16M ans their radit a nd 2a respectively. A body of mass m is fired straight from the surface of the larger star tpwards the surface of the smaller star. What should be its minimum intial speed to reach the surface of the smaller star? Obtain the expression in terms of G, M and a.
View Solution_S01_010_Q01.png)
A particle of mass m0 is projected from the surface of body (1) with initial velocity v0 towards the body (2). As shown in figure find the minimum value of v0 so that the particle reaches the surface of body (2). Radius of body (1) is R1 and mass of body (1) is M1. Radius body (2) is R2 and mass of the body (2) is M2 distance between te center the center of two bodies is D.
View SolutionThe distance between the centres of two stars is 10α. The masses of these stars are M and 16M and their radii α and 2α. A body of mass m is fired straight from the surface of the larger star towards the smaller star. What should be its minimum initial speed to reach the surface of teh smaller star? Obtain the expression interms of G, M and α.
View SolutionA charge particle of charge q & mass m is projected towards the center of uniformly charged ring of radius R& carrying a charge Qfrom a distance of √3R from the center along the axis,find the minimum value of velocity of projection (in ms ) so that particle reaches to x=−∞ where x - axis is along the axis of ring & center of ring is at origin.(given Q=6μc,q=3μc,m= 2gm,R=1m )
View SolutionTwo particles initially at rest move towards each other due to internal forces. Find the velocity of centre of mass when velocity of one particle is v and that of the other is 2v
View Solution