If a square frame of side L is made from a uniform wire and current I is flowing through it and its magnetic field intensity at the centre is B1. When the same current is passed through the circular loop whose circumference is same as that of the square, the magnetic field at the centre is B2. What will be B1/B2 ?
4√2π3
8√2π3
4√2π2
8√2π2
The correct Answer is:D
To solve the problem, we need to find the ratio B1B2, where B1 is the magnetic field intensity at the center of a square frame of side L carrying current I, and B2 is the magnetic field intensity at the center of a circular loop with the same current I and the same circumference as the square frame.
1. Calculate the Perimeter of the Square Frame:
The perimeter P of a square frame with side length L is given by:
P=4L
2. Determine the Radius of the Circular Loop:
The circumference C of the circular loop is equal to the perimeter of the square frame:
C=2πR=4L
Solving for R:
R=4L2π=2Lπ
3. Calculate the Magnetic Field B1 at the Center of the Square Frame:
The magnetic field at the center of a square loop carrying current I is given by:
B1=μ0I4π⋅4L⋅√2
Simplifying this:
B1=μ0I√2πL
4. Calculate the Magnetic Field B2 at the Center of the Circular Loop:
The magnetic field at the center of a circular loop carrying current I is given by:
B2=μ0I2R
Substituting R=2Lπ:
B2=μ0I2⋅2Lπ=μ0Iπ4L
5. Find the Ratio B1B2:
Now, we can find the ratio:
B1B2=μ0I√2πLμ0Iπ4L
Simplifying this:
B1B2=√2π4=4√2π
6. Final Result:
Thus, the ratio B1B2 is:
B1B2=8√2π2
The perimeter P of a square frame with side length L is given by:
P=4L
The circumference C of the circular loop is equal to the perimeter of the square frame:
C=2πR=4L
Solving for R:
R=4L2π=2Lπ
The magnetic field at the center of a square loop carrying current I is given by:
B1=μ0I4π⋅4L⋅√2
Simplifying this:
B1=μ0I√2πL
The magnetic field at the center of a circular loop carrying current I is given by:
B2=μ0I2R
Substituting R=2Lπ:
B2=μ0I2⋅2Lπ=μ0Iπ4L
Now, we can find the ratio:
B1B2=μ0I√2πLμ0Iπ4L
Simplifying this:
B1B2=√2π4=4√2π
Thus, the ratio B1B2 is:
B1B2=8√2π2
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)79videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)28videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Numerical Problems )18videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
Knowledge Check
- Question 1 - Select One
A square frame of side 1 m carries a current I, produces a magnetic field B at its centre. The same current is passed through a circular coil having the same perimeter as the square. The magnetic field at the centre of the circular coil is B'. The ratio B/B is
A8π2B8√2π2C16π2D16√2π2 - Question 2 - Select One
A square frame of side l carries a current produces a field B at its centre. The same current is passed through a circular loop having same perimeter as the square. The field at its centre is B', the ratio of B/B' is
A8√2π2B8π2C√2π2Dπ28√2 - Question 3 - Select One
A current I flows through a closed loop as shown in figure .The magnetic field at the centre O is
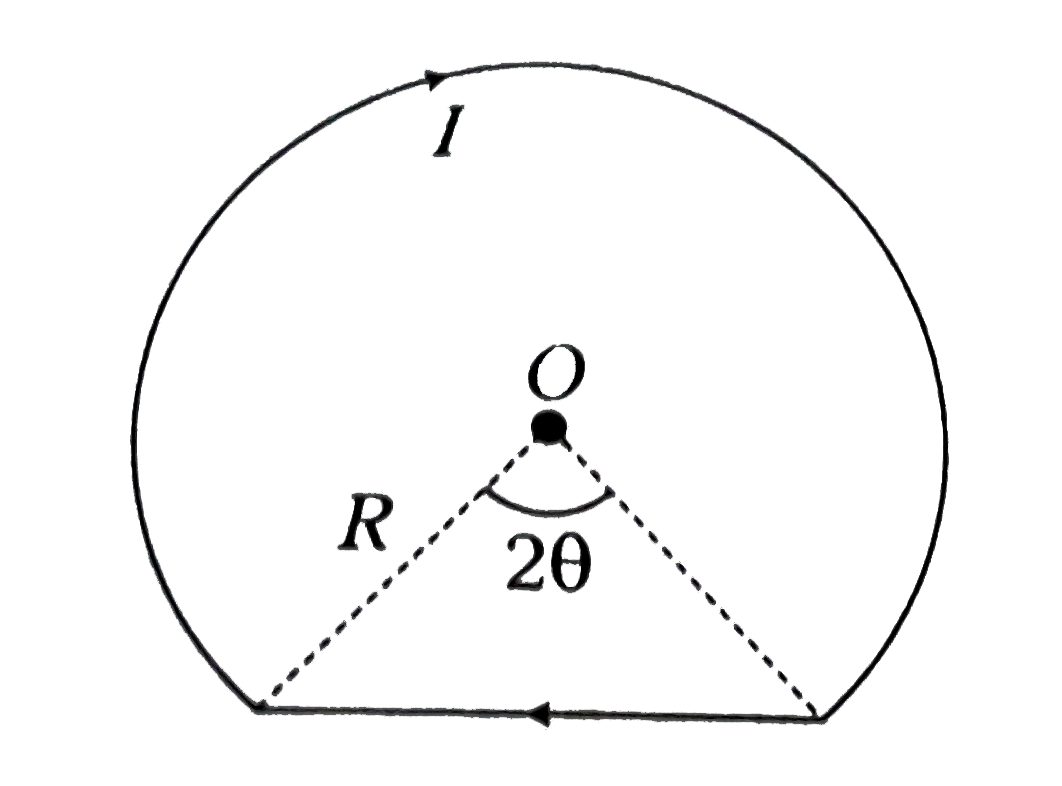 Aμ0I2πR(π−θ+tanθ)Bμ0I2πR(π−θ+sinθ)Cμ0I2πR(θ+sinθ)DNone of these
Aμ0I2πR(π−θ+tanθ)Bμ0I2πR(π−θ+sinθ)Cμ0I2πR(θ+sinθ)DNone of these
A steady current flows in a long wire. It is bent into a circular loop of one turn and the magnetic field at the center of the coil is B. If the same wire is bent into a circular loop of n turns, the magnetic field at the center of the coil is
View SolutionThe magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
View SolutionThe magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
View SolutionThe dipole moment of a circular loop carrying a current I, is m and the magnetic field at the centre of the loop is B1 . When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is B2 . The ratio B1B2 is:
View SolutionA square loop of edge 'a' carries a current l. The magnetic field at the centre of loop is
View Solution