If a wire of length 4 m and cross-sectional area of 2m2 is stretched by a force of 3 kN, then determine the change in length due to this force . Given, Young's modulus of material of wire is 110×109Nm−2
To determine the change in length (ΔL) of a wire when a force is applied, we can use the relationship between stress, strain, and Young's modulus. The formula we will use is:
Stress=Young's Modulus×Strain
Where:
- Stress (σ) = FA
- Strain (ε) = ΔLL
Rearranging the equation gives us:
ΔL=F⋅LA⋅Y
Where:
- F = applied force
- L = original length of the wire
- A = cross-sectional area
- Y = Young's modulus
Step 1: Identify the given values
- Length of the wire, L=4m
- Cross-sectional area, A=2m2
- Applied force, F=3kN=3000N
- Young's modulus, Y=110×109N/m2
Step 2: Substitute the values into the formula
Now, we can substitute the known values into the formula for ΔL:
ΔL=3000N⋅4m2m2⋅110×109N/m2
Step 3: Calculate the numerator
Calculate the numerator:
3000N⋅4m=12000N m
Step 4: Calculate the denominator
Calculate the denominator:
2m2⋅110×109N/m2=220×109N
Step 5: Calculate ΔL
Now, we can calculate ΔL:
ΔL=12000N m220×109N=12000220×109m
Calculating this gives:
ΔL≈54.545×10−6m
Step 6: Convert to mm
To convert meters to millimeters, we multiply by 1000:
ΔL≈54.545μm≈0.0545mm
Final Answer
The change in length of the wire due to the applied force is approximately:
ΔL≈54.5μm
- Stress (σ) = FA
- Strain (ε) = ΔLL
- F = applied force
- L = original length of the wire
- A = cross-sectional area
- Y = Young's modulus
- Length of the wire, L=4m
- Cross-sectional area, A=2m2
- Applied force, F=3kN=3000N
- Young's modulus, Y=110×109N/m2
Now, we can substitute the known values into the formula for ΔL:
Calculate the numerator:
Calculate the denominator:
Now, we can calculate ΔL:
To convert meters to millimeters, we multiply by 1000:
The change in length of the wire due to the applied force is approximately:
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Check point 12.1
15 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Check point 12.2
15 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Level 2 Subjective
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
434 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A body of mass 3.14 kg is suspended from one end of a non uniform wire of length 10m, such that the radius of the wire is changing uniformly from 9.8×10−4 m at one end to 5×10−4 m at the other end. Find the change in length of the wire in mm. Young's modulus of the material of the wire is 2×1011N/m2 (mass of wire is negligible)
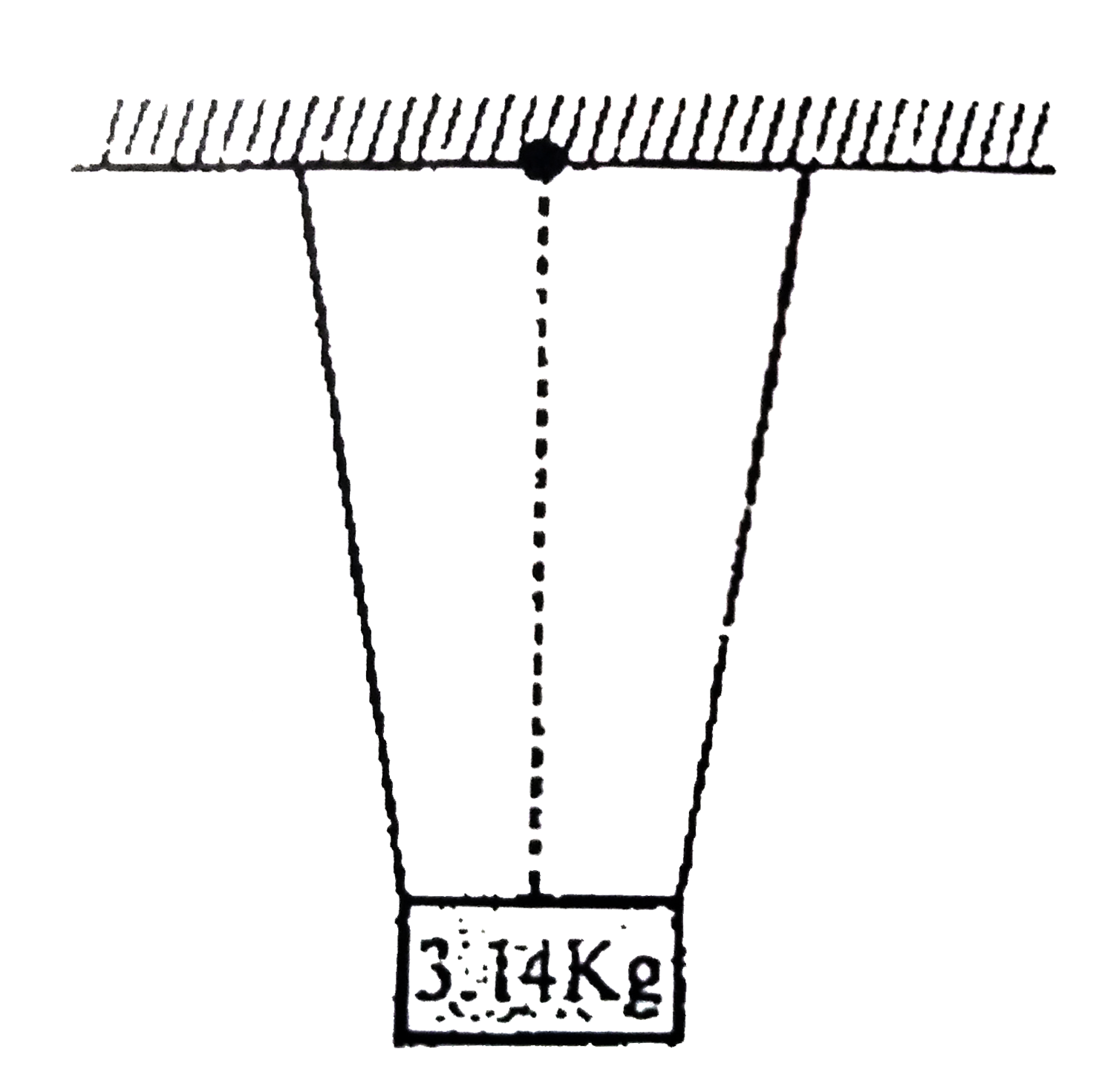
View SolutionA steel wire of length 3.0m is stretched through 3.0 mm. the cross-sectional area of the wire is 5.0mm2. Calculate the elastic potential energy stroed in the wire in the stretched condition. Young's modulus of steel is 2.0×1011Nm−2.
View Solution
Knowledge Check
If a wire of length 4 m and cross-sectional area of 2 m2 is stretched by a force of 3 kN, then determine the change in length due to this force, Given, Young's modulus of material of wire is 110×109Nm−2
A60.2×10−3mmB54.5×10−6mmC56.4×10−3mmD62.5×10−3mmA wire of length 10 m and cross-section are 10−6m2 is stretched with a force of 20 N. If the elongation is 1 mm, the Young's modulus of material of the wire will be
A1010N/m2B1011N/m2C2×1010N/m2D2×1011N/m2A wire 3m long and having cross - sectional area of 0.42m2 is found to stretched by 0.2 m under a tension of 1000 N. The value of young's modulus for the material of the wire is
A4.6×104N/m2B3.6×104N/m2C4×104N/m2D6.6×10−4N/m2
When a wire 2 m long and 0.05cm2 in cross-section is stretched by a mass of 2 kg, it increases in length by 0.04 mm. Young's modulus of the material of the wire is
(g=10ms−2)
View SolutionA metal wire 4m long and 2×10−7sq.m in cross-section is streched by a force of 30N. If the work done in streching that wire is 4.5×10−2J the young's modulus of the wire is
View SolutionA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the torce corstant of the wire is
View SolutionA wire suspended vertically from one of its ends is stretched by attaching a weight of 20 N to its lower end. If its length changes by 1% and if the Young's modulus of the material of the wire is 2×1011N/m2, then the area of cross section of the wire is
View SolutionA wire of 10m long and 1mm2 area of cross section is strechted by a force of 20N. If the elongation is 2mm the young's modulus of the material of the wire (in Pa) is
View Solution
