A bar of mass m and length l is hanging from point A as shown in figure.Find the increase in its length due to its own weight. The young's modulus of elasicity of the wire is Y and area of cross-section of the wire is A.

Video Solution

Text Solution

Verified by Experts

Consider a small section dx of the bar at a distance x from B. The weight of the bar for a length x is,

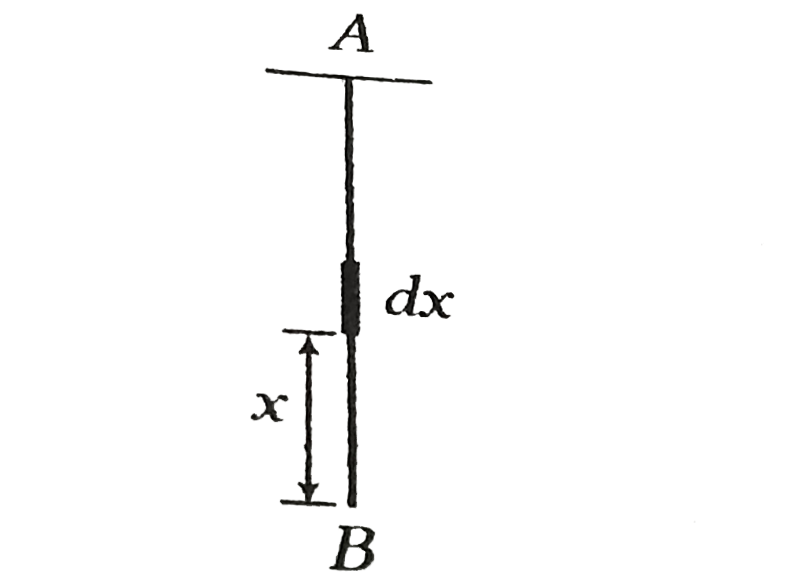
$w = (\frac{m g}{l}) x$
Elongation in section dx will be, $d l = (\frac{w}{A Y}) d x = (\frac{m g}{l A Y}) x d x$
Total elongation in the bar can be obtained by integrating this expression for x=0 to x=l.
$∴ Δ l = \int_{x = 0}^{x = 1} d l = (\frac{m g}{l A Y}) \int_{0}^{1} x d x$
or Increase in length, $Δ l = \frac{m g l}{2 A Y}$

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A thick rope of density $ρ$ and length $L$ is hung from a rigid support. The increase in length of the rope due to its own weight is ( $Y$ is the Young's modulus)
A $\frac{0.1}{4 Y} ρ L^{2} g$
B $\frac{1}{2 Y} ρ L^{2} g$
C $\frac{ρ L^{2} g}{Y}$
D $\frac{ρ L g}{Y}$
Question 2 - Select One
A wire of mass m and length l is suspended from a ceiling. Due to its own wieght it elongates, consider cross-section are of wire as A ans Young's modulus of material of wire as Y. Th eelongation in the wire is
A $\frac{2 m g}{3 Y A}$
B $\frac{m g l}{Y A}$
C $\frac{m g l}{2 Y A}$
Dcannot be calcuated
Question 3 - Select One
A wire suspended vertically from one of its ends is stretched by attaching a weight of 20 N to its lower end. If its length changes by 1% and if the Young's modulus of the material of the wire is $2 \times 10^{11} N / m^{2}$ , then the area of cross section of the wire is
A $1 m m^{2}$
B $10^{- 1} m m^{2}$
C $10^{- 2} m m^{2}$
D $10^{- 3} m m^{2}$

DC PANDEY-ELASTICITY-Example

Home
Ask Doubt
Profile